河北省石家庄市正定县2020-2021学年七年级下学期数学期中试卷

试卷更新日期：2021-06-17 类型：期中考试

进入出卷网下载

一、选择题（共16小题）.

1. 下列四幅图中，∠1和∠2是同位角的是（）

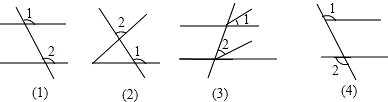A、（1）、（2） B、（3）、（4） C、（1）、（2）、（3） D、（2）、（3）、（4）

查看试题解析
2. 计算正确的是（）

A、（﹣5）⁰=0 B、x²+x³=x⁵ C、（ab²）³=a²b⁵ D、2a²•a^﹣¹=2a

查看试题解析
3. 用科学记数法表示的数﹣1.96×10⁴ ，则它的原数是（）

A、19600 B、﹣1960 C、196000 D、﹣19600

查看试题解析
4. 如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（　　）

A、∠3＝∠A B、∠1＝∠2 C、∠D＝∠DCE D、∠D+∠ACD＝180°

查看试题解析
5. 墨迹覆盖了等式“x³ x＝x²（x≠0）”中的运算符号，则覆盖的是（）

A、+ B、﹣ C、× D、÷

查看试题解析
6. 将9.5²变形正确的是（）

A、9.5²=9²+0.5² B、9.5²=（10+0.5）（10﹣0.5） C、9.5²=10²﹣2×10×0.5+0.5² D、9.5²=9²+9×0.5+0.5²

查看试题解析
7. 如图，在平面内作已知直线m的垂线，可作垂线的条数有（）

A、0条 B、1条 C、2条 D、无数条

查看试题解析
8. 利用加减消元法解方程组 ${\begin{matrix} 2 x + 5 y = - 10 ① \\ 5 x - 3 y = 6 ② \end{matrix}$ ，下列做法正确的是（）

A、要消去y，可以将①×5+②×2 B、要消去x，可以将①×3+②×（﹣5） C、要消去y，可以将①×5+②×3 D、要消去x，可以将①×（﹣5）+②×2

查看试题解析

9. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、

\frac{x}{4} + \frac{y}{3} = \frac{42}{60}

B、

\frac{x}{5} + \frac{y}{4} = \frac{42}{60}

C、

\frac{x}{4} + \frac{y}{5} = \frac{42}{60}

D、

\frac{x}{3} + \frac{y}{4} = \frac{42}{60}

查看试题解析

10. 把一块直尺与一块三角板如图放置，若∠1＝40°，则∠2的度数为（）

A、130° B、140° C、120° D、125°

查看试题解析
11. 方程2x﹣ $\frac{1}{y}$ =0，3x+y=0，2x+xy=1，3x+y﹣2x=0，x²﹣x+1=0中，二元一次方程的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，AB∥EF∥CD，EG∥DB，则图中与∠1相等的角（∠1除外）共有（）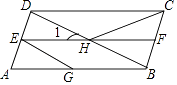

A、6个 B、5个 C、4个 D、3个

查看试题解析
13. 选择计算（﹣2x+3y）（2x+3y）的最佳方法是（）

A、运用多项式乘多项式法则 B、运用平方差公式 C、运用单项式乘多项式法则 D、运用完全平方公式

查看试题解析
14. 已知a，b满足方程组 ${\begin{cases} a + 2 b = 8 \\ 2 a + b = 7 \end{cases}$ ，则a﹣b的值为（）

A、﹣1 B、0 C、1 D、2

查看试题解析
15. 如图，原来是重叠的两个直角三角形，将其中一个三角形沿着BC方向平移线段BE的距离，就得到此图形，下列结论正确的有（）
①AC∥DF；②HE＝5；③CF＝5；④阴影部分面积为 $\frac{55}{2}$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
16. 观察下列各式及其展开式：
（a+b）²=a²+2ab+b²
（a+b）³=a³+3a²b+3ab²+b³
（a+b）⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
…
请你猜想（a+b）¹⁰的展开式第三项的系数是（　　）

A、36 B、45 C、55 D、66

查看试题解析

二、填空题（本大题共4个小题，每小题3分，共12分，把答案写在题中横线上）

17. 若x²+mx+16是完全平方式，则m＝．

查看试题解析
18. 把命题“平行于同一条直线的两条直线平行”改成如果…那么的形式．

查看试题解析
19. 已知2x+5y＝1，则4^x•32^y的值为．

查看试题解析
20. 现用190张铁皮做盒，一张可以做8个盒身或22个盒底，1个盒身与2个盒底配一个盒子，问用多少张铁皮制盒身、多少张铁皮制盒底，可制成一批完整的盒子？若设用x张铁皮制盒身，y张铁皮制盒底，列方程组为．

查看试题解析

三、解答题（本大题共6个小题，共56分.解答应写出文字说明、证明过程或演算步骤）

21.

(1)、（2ab²）³﹣（9ab²）（﹣ab²）²；

(2)、解方程组 ${\begin{cases} x + 3 y = 8 \\ 5 x - 4 y = 2 \end{cases}$ ．

(3)、 $- 1^{2006} + {(- \frac{1}{2})}^{- 2} - {(3.14 - π)}^{0}$ ；

查看试题解析
22. 已知x²﹣3x＝1，求代数式（x﹣1）（3x+1）﹣（x+2）²﹣4的值．

查看试题解析
23. 完成推理过程：如图．
∵∠1＝∠2（已知），∠2＝∠4（        ）

∴∠4＝∠1（        ）

∴DB∥CE（       ）

∴∠C＝∠ABD（        ）

∵∠C＝∠D（已知）

∴∠D＝∠ABD（        ）

∴AC∥DF（        ）

查看试题解析
24. 作图题：在方格纸中，将△ABC向右平移4个单位得到△A₁B₁C₁

(1)、画出△A₁B₁C₁ ．

(2)、∠CAB＝70°，∠CBA＝54°，求∠CBC₁得度数．

查看试题解析
25. 已知：用2辆A型车和1辆B型车载满货物一次可运货10吨；用1辆A型车和2辆B型车载满货物一次可运货11吨，某物流公司现有26吨货物，计划A型车a辆，B型车b辆，一次运完，且恰好每辆车都载满货物．
根据以上信息，解答下列问题：

(1)、1辆A型车和1辆车B型车都载满货物一次可分别运货多少吨？

(2)、请你帮该物流公司设计租车方案：

(3)、若A型车每辆需租金100元/次，B型车每辆需租金120元/次．请选出最省钱车方案，并求出最少租车费．

查看试题解析
26. 综合与探究：
将三角形纸板如图放置，点P是边AB边上一点，DF∥CE，∠PCE＝∠α，∠PDF＝∠β，

(1)、探究：如果α＝30°，β＝40°，则∠DPC＝．

(2)、猜想：当点P在E、F两点之间运动时，∠DPC与α、β之间有何数量关系？并说明理由；

(3)、拓展：如果点P在E、F两点外侧运动时（点P与点A、B、E、F四点不重合），上述（2）中的结论是否还成立？并说明理由．

查看试题解析