广东省深圳市南山2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-06-17 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 计算:a2•a5=( )A、a B、7a C、a10 D、a72. 下列各式中不能用平方差公式进行计算的是( )A、(m﹣n)(m+n) B、(﹣x﹣y)(﹣x﹣y) C、(x4﹣y4)(x4+y4) D、(a3﹣b3)(b3+a3)3. 若(ambn)2=a8b6 , 那么m2﹣2n的值是( )A、10 B、52 C、20 D、324. 已知(x﹣2015)2+(x﹣2017)2=34,则(x﹣2016)2的值是( )A、4 B、8 C、12 D、165. 如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形.(a>0)剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙)则矩形的面积为( )
 A、(2a2+5a)cm2 B、(3a+15)cm2 C、(6a+9)cm2 D、(6a+15)cm26. 下列四幅图中,∠1和∠2是同位角的是( )
A、(2a2+5a)cm2 B、(3a+15)cm2 C、(6a+9)cm2 D、(6a+15)cm26. 下列四幅图中,∠1和∠2是同位角的是( )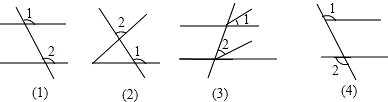 A、(1)、(2) B、(3)、(4) C、(1)、(2)、(3) D、(2)、(3)、(4)7. 下列说法:①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.正确的个数有( )个.
A、(1)、(2) B、(3)、(4) C、(1)、(2)、(3) D、(2)、(3)、(4)7. 下列说法:①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.正确的个数有( )个.
A、1 B、2 C、3 D、48. 下列图象不能反映y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 9. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )A、
9. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度,下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )A、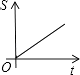 B、
B、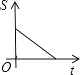 C、
C、 D、
D、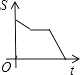 10. 如图,OP∥QR∥ST,则下列各式中正确的是( )
10. 如图,OP∥QR∥ST,则下列各式中正确的是( )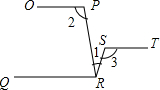 A、∠1+∠2+∠3=180° B、∠1+∠2﹣∠3=90° C、∠1﹣∠2+∠3=90° D、∠2+∠3﹣∠1=180°
A、∠1+∠2+∠3=180° B、∠1+∠2﹣∠3=90° C、∠1﹣∠2+∠3=90° D、∠2+∠3﹣∠1=180°二、填空题(每题3分,共15分)
-
11. 新型冠状病毒是依靠飞沫和直接接触传播,所以我们要带好口罩做好防护.其中飞沫的直径大约为0.00000301米,数0.00000301用科学记数法表示为.12. 如图,直线a,b,a∥b,点C在直线b上,∠DCB=90°,若∠1=70°,则∠2的度数为 .
 13. 已知三角形ABC,且AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,那么x的取值范围是 .14. 如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有 .
13. 已知三角形ABC,且AB=3厘米,BC=2厘米,A、C两点间的距离为x厘米,那么x的取值范围是 .14. 如图所示,在△ABC中,∠1=∠2,G是AD的中点,延长BG交AC于点E,F为AB上一点,CF⊥AD交AD于点H.①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;③CH为△ACD的边AD上的高;④AH是△ACF的角平分线和高线,其中判断正确的有 .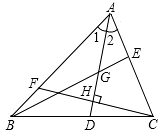 15. 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,第n次操作后,得到△AnBn∁n , 要使△AnBn∁n的面积超过2020,则至少需要操作次.
15. 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1 , B1 , C1 , 使A1B=AB,B1C=BC,C1A=CA,顺次连接A1 , B1 , C1 , 得到△A1B1C1 . 第二次操作:分别延长A1B1 , B1C1 , C1A1至点A2 , B2 , C2 , 使A2B1=A1B1 , B2C1=B1C1 , C2A1=C1A1 , 顺次连接A2 , B2 , C2 , 得到△A2B2C2 , …按此规律,第n次操作后,得到△AnBn∁n , 要使△AnBn∁n的面积超过2020,则至少需要操作次.
三、解答题(共55分)
-
16. 计算:(1)、2(a4)3+(a3)2•(a2)3﹣a2•a10;(2)、(﹣1)2012+ ﹣(3.14﹣π)0;(3)、(x﹣1)(x2+x+1)﹣x(x+1)(x﹣1);(4)、(2x3y)2•(﹣2xy)+(﹣2x2y)3÷(2x2).17. 先化简再求值:[(3a+b)2﹣(b+3a)(3a﹣b)﹣6b2]÷(﹣2b),其中a=﹣ ,b=﹣2.18. 已知∠BAC,点D是AC边上一点,按要求画图,只保留作图痕迹,不写作图过程.
 (1)、用尺规作图在AC的右侧以点D为顶点作∠CDP=∠CAB;(2)、射线DP与AB的位置关系为 , 理由是 ;(3)、画出表示点D到AB的距离的线段和表示点B到AC的距离的线段.19. 周老师为锻炼身体一直坚持步行上下班.已知学校到周老师家总路程为2000米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示.
(1)、用尺规作图在AC的右侧以点D为顶点作∠CDP=∠CAB;(2)、射线DP与AB的位置关系为 , 理由是 ;(3)、画出表示点D到AB的距离的线段和表示点B到AC的距离的线段.19. 周老师为锻炼身体一直坚持步行上下班.已知学校到周老师家总路程为2000米.一天,周老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.周老师回家过程中,离家的路程S(米)与所用时间t(分)之间的关系如图所示. (1)、求a的值.(2)、b= ;c= .(3)、求周老师从学校到家的平均速度.20. 已知:如图,点A,C,F,E在同一条直线上,AF=EC,AB=ED,BC=DF,
(1)、求a的值.(2)、b= ;c= .(3)、求周老师从学校到家的平均速度.20. 已知:如图,点A,C,F,E在同一条直线上,AF=EC,AB=ED,BC=DF,求证:AB∥ED.
 21. 把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法通常被称为配方法.配方法在代数式求值、解方程、最值问题等都有着广泛的应用.
21. 把代数式通过配凑等手段,得到完全平方式,再运用完全平方式是非负性这一性质增加问题的条件,这种解题方法通常被称为配方法.配方法在代数式求值、解方程、最值问题等都有着广泛的应用.例如:若代数式M=a2﹣2ab+2b2﹣2b+2,利用配方法求M的最小值:a2﹣2ab+2b2﹣2b+2=a2﹣2ab+b2+b2﹣2b+1+1=(a﹣b)2+(b﹣1)2+1.
∵(a﹣b)2≥0,(b﹣1)2≥0,
∴当a=b=1时,代数式M有最小值1.
请根据上述材料解决下列问题:
(1)、在横线上添上一个常数项使之成为完全平方式:a2+4a+;(2)、若代数式M= +2a+1,求M的最小值;(3)、已知a2+2b2+4c2﹣2ab﹣2b﹣4c+2=0,求代数式a+b+c的值.22. 已知:如图(1)直线AB、CD被直线MN所截,∠1=∠2.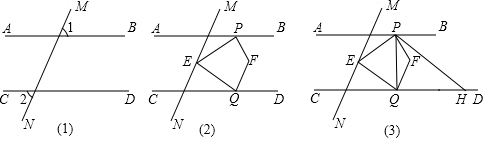 (1)、求证:AB∥CD;(2)、如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)、如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.
(1)、求证:AB∥CD;(2)、如图(2),点E在AB,CD之间的直线MN上,P、Q分别在直线AB、CD上,连接PE、EQ,PF平分∠BPE,QF平分∠EQD,则∠PEQ和∠PFQ之间有什么数量关系,请直接写出你的结论;(3)、如图(3),在(2)的条件下,过P点作PH∥EQ交CD于点H,连接PQ,若PQ平分∠EPH,∠QPF:∠EQF=1:5,求∠PHQ的度数.