广东省广州名校2020-2021学年七年级下学期数学期中试卷

试卷更新日期：2021-06-17 类型：期中考试

进入出卷网下载

一、选择题（共10小题）.

1. 下列各点中，在第四象限的是（）

A、（﹣2，﹣3） B、（﹣3，2） C、（3，2） D、（3，﹣2）

查看试题解析
2. 在实数﹣5，0.2， $\frac{1}{7}$ ， $\sqrt{2}$ ，﹣π， $^{3} \sqrt{9}$ 中，无理数的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{{(- 3)}^{2}}$ ＝﹣3 B、 $^{3} \sqrt{- 5}$ ＝ $^{3} \sqrt{5}$ C、 $\sqrt{36}$ ＝±6 D、 $- \sqrt{0.36}$ ＝﹣0.6

查看试题解析
4. 如图，CE是△ABC的角平分线，EF∥BC，交AC于点F．已知∠AFE＝68°，则∠FEC的度数为（）

A、68° B、34° C、32° D、22°

查看试题解析
5. 如图，AO⊥BO，垂足为点O，直线CD经过点O，下列结论正确的是（）

A、∠1+∠2＝180° B、∠1﹣∠2＝90° C、∠1﹣∠3＝∠2 D、∠1+∠2＝90°

查看试题解析
6. 某船往返两地，顺流时每小时航行18千米，逆流时每小时航行14千米，则水流速度是多少？（）

A、3.5千米/时 B、2.5千米/时 C、2千米/时 D、3千米/时

查看试题解析
7. 下列命题是假命题的是（）

A、两条直线被第三条直线所截，内错角相等 B、实数和数轴上的点是一一对应的 C、坐标平面内的点与有序实数对是一一对应的 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
8. 已知在第四象限的点P的坐标为（2﹣a，3a+6），且点P到两坐标轴的距离相等，则点P的坐标是（）

A、（3，3） B、（6，﹣6） C、（6，6）或（3，﹣3） D、（6，﹣6）或（3，3）

查看试题解析
9. 已知关于x，y的二元一次方程组 ${\begin{cases} ax-by=4 \\ a x + b y = 2 \end{cases}$ 的解 ${\begin{cases} x = 2 \\ y = 1 \end{cases}$ ，则2a﹣3b的值为（）

A、﹣6 B、4 C、6 D、﹣4

查看试题解析
10. 如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点A₁(﹣1，1)，第二次向右跳动3个单位至点A₂(2，1)，第三次跳动至点A₃(﹣2，2)，第四次向右跳动5个单位至点A₄(3，2)，…，以此规律跳动下去，点A第2020次跳动至点A₂₀₂₀的坐标是（）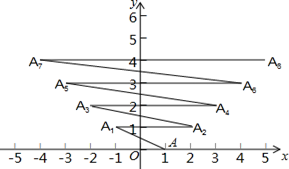

A、(1012，1011) B、(1009，1008) C、(1010，1009) D、(1011，1010)

查看试题解析

二、填空题（共6小题，每小题3分，共18分）

11. $\sqrt{3} （ \sqrt{3} + \frac{1}{\sqrt{3}} ）$ ＝．

查看试题解析
12. 如果点P（m+3，m﹣2）在x轴上，那么点P的坐标为．

查看试题解析
13. 如图，AB∥CD，AB⊥AE，∠CAE＝42°，则∠ACD的度数为.

查看试题解析
14. 如图，圆的直径为1个单位长度，该圆上的点A与数轴上表示﹣1的点重合，将该圆沿数轴滚动1周，点A到达点B的位置，则点B表示的数是．

查看试题解析
15. 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G，D、C分别在M、N的位置上，若∠EFG＝50°，则∠2﹣∠1＝．

查看试题解析
16. 已知y＝ $\sqrt{（ x- 4 ）^{2}}$ ﹣x+5，当x分别取1、2、3、…、2021时，所对应y值的总和是．

查看试题解析

三、解答题（共8题，共72分，解答应写出文字说明、证明过程或演算步骤）

17. 解方程组：

(1)、 ${\begin{cases} y = x + 3 \\ 7 x + 5 y = 9 \end{cases}$ ；

(2)、 ${\begin{cases} 2 x - y = 5 \\ x + 3 y = - 1 \end{cases}$ ．

查看试题解析
18. 已知：如图所示，AB∥CD，BC∥DE．求证：∠B+∠D＝180°．

查看试题解析
19. 在平面直角坐标系中有三点A（﹣2，3），B（2，0），C（4，5）．

(1)、请在平面直角坐标系中描出A，B，C三点；

(2)、点C可以由点B向平移个单位长度，再向平移个单位长度得到；

(3)、求三角形ABC的面积．

查看试题解析
20. 某旅行社组织200人去中山纪念堂和白云山旅游，到中山纪念堂的人数比到白云山的人数的2倍少1，到两地旅游的人数各是多少？

查看试题解析
21. 已知a的立方根是2，b是 $\sqrt{5}$ 的整数部分，c是9的平方根，求a+b+2c的算术平方根．

查看试题解析
22. 如图，直线AB、CD相交于点O，已知∠BOD＝75°，OE把∠AOC分成两个角，且∠AOE：∠EOC＝2：3．

(1)、求∠AOE的度数；

(2)、射线OF从OE出发，绕点O逆时针旋转α（0°＜α＜180°），如图2，当OF平分∠BOE时，求∠DOF的度数．

查看试题解析
23. 如图，有一个面积为400cm²的正方形．

(1)、正方形的边长是多少？

(2)、若沿此正方形边的方向剪出一个长方形，能否使剪出的长方形纸片的长宽之比为5：4，且面积为360cm²？若能，试求出剪出的长方形纸片的长与宽；若不能，试说明．

查看试题解析
24. 如图，已知AB∥CD，∠ACD的平分线与AB交于点E．

(1)、求证：∠ACE＝∠AEC；

(2)、若点F为射线CE上一点．
①连接FA，探究∠FCD、∠FAB和∠AFC之间的数量关系，并证明你的结论；

②点G为线段CE上一点且∠CAG＝3∠EAG，当∠GAF+∠AEC＝90°时，求 $\frac{∠ C A F}{∠ E A F}$ 的值．

查看试题解析
25. 已知在平面直角坐标系中，O为坐标原点，点A的坐标为（0，a），点B的坐标为（﹣3，b），点C的坐标为（c，a﹣2），其中a，b满足 $| 3 a - 2 b - 11 | + \sqrt{a - 2 b - 9} = 0$ ．

(1)、求点A、B的坐标．

(2)、若点C在y轴上，求三角形ABC的面积．

(3)、是否存在点C，使得三角形ABC的面积等于10？如果存在，请求出c的值；如果不存在，请说明理由．

查看试题解析