北京市海淀区2020-2021学年七年级下学期数学期中试卷（五四学制）
试卷更新日期：2021-06-17 类型：期中考试
一、选择题（本题共30分，每小3分）下面各题均有四个选项，正确的选项只有一个．
-
1. 以下国产新能源电动车的车标图案不是轴对称图形的是（ ）A、
北汽新能源
B、
长城新能源
C、
东风新能源
D、
江淮新能源
2. 计算 的结果是（ ）A、 B、 C、 D、3. 下列计算正确的是（ ）A、x+x2＝x3 B、x2•x2＝x3 C、x9÷x3＝x3 D、（x3）2＝x64. 如图，AB＝AC，点D，E分别在AB，AC上，补充下列一个条件后，不能判断△ABE≌△ACD的是（ ）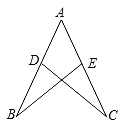
A、∠B＝∠C B、AD＝AE C、∠BDC＝∠CEB D、BE＝CD5. 下列等式中，从左到右的变形是因式分解的是（ ）A、x2+3x+2＝（x+1）（x+2） B、3x2﹣3x+1＝3x（x﹣1）+1 C、m（a+b）＝ma+mb D、（a+2）2＝a2+4a+46. 如图，△ABC中，∠A＝40°，AB的垂直平分线分别交AB，AC于点D，E，连接BE，则∠BEC的大小为（ ）
A、40° B、50° C、80° D、100°7. 如图，在△ABC中，AB＝3，AC＝4，BC＝5，EF是BC的垂直平分线，P是直线EF上的任意一点，则PA+PB的最小值是（ ）
A、3 B、4 C、5 D、68. 如图，每个小方格的边长为1，A ， B两点都在小方格的顶点上，点C也是图中小方格的顶点，并且△ABC是等腰三角形，那么点C的个数为（ ）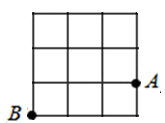
A、1 B、2 C、3 D、49. 如图，已知∠MON及其边上一点A．以点A为圆心，AO长为半径画弧，分别交OM，ON于点B和C．再以点C为圆心，AC长为半径画弧，恰好经过点B．错误的结论是（ ）
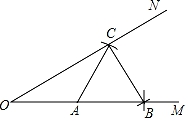A、S△AOC＝S△ABC B、∠OCB＝90° C、∠MON＝30° D、OC＝2BC10. 已知OP平分∠AOB，点Q在OP上，点M在OA上，且点Q，M均不与点O重合．在OB上确定点N，使QN＝QM，则满足条件的点N的个数为（ ）A、1个 B、2个 C、1或2个 D、无数个二、填空题（本题共24分，每小题3分）
-
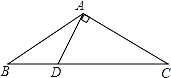
11. 因式分解：a3﹣9a＝ ．12. 计算：（2a）3•（﹣a）4÷a2＝ ．13. 点M（3，﹣4）关于x轴的对称点的坐标是 ．14. 若等腰三角形的一个内角为50°，则它的底角的度数为 ．15. 如图，△ABC中，AB＝AC，∠BAC＝120°，AD⊥AC交BC于点D，AD＝3，则BC＝ ．
16. 育英学校四初二数学兴趣小组的小桃桃同学提出这样一个问题：如图，从边长为a+4的正方形纸片中剪去一个边长为a的正方形（a＞0），剩余部分沿虚线剪开，拼成一个长方形（不重叠无缝隙），你认为长方形的面积为 ．
17. 如图，在△ABC中，∠C＝90°，以点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 MN的长为半径画弧，两弧交于点P，作射线AP交BC于点D，若CD＝1，AB＝4，则△ABD的面积是 ．
18. 我国古代数学的许多创新与发展都曾居世界前列，其中“杨辉三角”（如图）就是一例，它的发现比欧洲早五百年左右．杨辉三角两腰上的数都是1，其余每个数为它的上方（左右）两数之和，事实上，这个三角形给出了（a+b）n（n＝1，2，3，4，5，6）的展开式（按a的次数由大到小的顺序排列）的系数规律．例如，在三角形中第三行的三个数1，2，1，恰好对应着（a+b）2＝a2+2ab+b2展开式中各项的系数；第四行的四个数1，3，3，1，恰好对应着（a+b）3＝a3+3a2b+3ab2+b3展开式中各项的系数，等等．
(1)、当n＝4时，（a+b）4的展开式中第3项的系数是；(2)、人们发现，当n是大于6的自然数时，这个规律依然成立，那么（a+b）7的展开式中各项的系数的和为 ．三、解答题（本大题共46分，第19题8分，每个小题各4分，20～22题每题5分，第23题6分，第24题5分，第25-26题6分）
-
19.(1)、计算：（3﹣π）0﹣38÷36+ ；(2)、因式分解：3x2﹣12y2 ．20. 如图，已知AB＝AC，E为AB上一点，ED∥AC，ED＝AE．求证：BD＝CD．
21. 已知2a2+3a﹣4＝0，求代数式3a（2a+1）﹣（2a+1）（2a﹣1）的值．22. 如图所示的正方形网格中，每个小正方形的边长都为1，△ABC的顶点都在网格线的交点上，点B关于y轴的对称点的坐标为（2，0），点C关于x轴的对称点的坐标为（﹣1，﹣2）．
(1)、根据上述条件，在网格中建立平面直角坐标系xOy；(2)、画出△ABC分别关于y轴的对称图形△A1B1C1；(3)、写出点A关于x轴的对称点的坐标．23. 如图，已知△ABC．
(1)、尺规作图：过点C作AB的垂线交AB于点O．不写作法，保留作图痕迹；(2)、分别以直线AB，OC为x轴，y轴建立平面直角坐标系，使点B，C均在正半轴上．若AB＝7.5，OC＝4.5，∠A＝45°，写出点B关于y轴的对称点D的坐标；(3)、在（2）的条件下，求△ACD的面积．24. 阅读图中的材料：
利用分组分解法解决下面的问题：
(1)、分解因式：x2﹣2xy+y2﹣4；(2)、已知△ABC的三边长a，b，c满足a2﹣ab﹣ac+bc＝0，判断△ABC的形状并说明理由．25. 如图，在等边三角形ABC右侧作射线CP，∠ACP＝α（0＜α＜60°），点A关于射线CP的对称点为点D，BD交CP于点E，连接AD，AE．
(1)、求∠DBC的大小（用含α的代数式表示）；(2)、在α（0°＜α≤60°）的变化过程中，∠AEB的大小是否发生变化？如果发生变化，请直接写出变化的范围；如果不发生变化，请直接写出∠AEB的大小；(3)、用等式表示线段AE，BD，CE之间的数量关系，并证明．26. 对于△ABC及其边上的点P，给出如下定义：如果点M1 ， M2 ， M3 ， ……，Mn都在△ABC的边上，且PM1＝PM2＝PM3＝……＝PMn ， 那么称点M1 ， M2 ， M3 ， ……，Mn为△ABC关于点P的等距点，线段PM1 ， PM2 ， PM3 ， ……，PMn为△ABC关于点P的等距线段．
(1)、如图1，△ABC中，∠A＜90°，AB＝AC，点P是BC的中点．①点B，C ▲ △ABC关于点P的等距点，线段PA，PB ▲ △ABC关于点P的等距线段；（填“是”或“不是”）
②△ABC关于点P的两个等距点M1 ， M2分别在边AB，AC上，当相应的等距线段最短时，在图1中画出线段PM1 ， PM2；
(2)、△ABC是边长为4的等边三角形，点P在BC上，点C，D是△ABC关于点P的等距点，且PC＝1，求线段DC的长；(3)、如图2，在Rt△ABC中，∠C＝90°，∠B＝30°．点P在BC上，△ABC关于点P的等距点恰好有四个，且其中一个是点C．若BC＝a，直接写出PC长的取值范围．（用含a的式子表示）