北京市大兴区2020-2021学年七年级下学期数学期中试卷
试卷更新日期:2021-06-17 类型:期中考试
一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,正确的选项只有一个。
-
1. 下面 与 不是对顶角的是( )A、
 B、
B、 C、
C、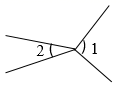 D、
D、 2. 16 的算术平方根是( )A、 ±8 B、8 C、±4 D、43. 下面的每组图形中,平移左图可以得到右图的是( )A、
2. 16 的算术平方根是( )A、 ±8 B、8 C、±4 D、43. 下面的每组图形中,平移左图可以得到右图的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,∠1与∠2是同旁内角的是( )A、
4. 下列图形中,∠1与∠2是同旁内角的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列等式正确的是( )A、 =﹣3 B、 =± C、 =4 D、- =﹣6. 下列命题:①直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;②经过直线外一点,有且只有一条直线与这条直线平行; ③垂线段最短;④同旁内角互补.其中,真命题有( )A、3个 B、2个 C、1个 D、0个7. 在平面直角坐标系xOy中,点P在第二象限,且点P到x轴的距离是4,到y轴的距离是5,则点P坐标是( )A、(﹣5,4) B、(﹣4,5) C、(4,5) D、(5,﹣4)8. 如图,数轴上有A,B,C,D四点,则所表示的数与5﹣ 最接近的是( )
5. 下列等式正确的是( )A、 =﹣3 B、 =± C、 =4 D、- =﹣6. 下列命题:①直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;②经过直线外一点,有且只有一条直线与这条直线平行; ③垂线段最短;④同旁内角互补.其中,真命题有( )A、3个 B、2个 C、1个 D、0个7. 在平面直角坐标系xOy中,点P在第二象限,且点P到x轴的距离是4,到y轴的距离是5,则点P坐标是( )A、(﹣5,4) B、(﹣4,5) C、(4,5) D、(5,﹣4)8. 如图,数轴上有A,B,C,D四点,则所表示的数与5﹣ 最接近的是( ) A、点A B、点B C、点C D、点D
A、点A B、点B C、点C D、点D二、填空题(本题共16分,每小题2分)
-
9. 2的平方根是 .10. 实数 ,0, ,3.14159, , ,0.010010001……(相邻两个1之间依次多一个0),其中,无理数有个.11. 如图,直线AB,CD相交于点O,EO⊥AB,垂足为点O,若∠AOD=132°,则∠EOC=°.
 12. 如图,要把池中的水引到 处,且使所开渠道最短,可过 点作 于 ,然后沿所作的线段 开渠,所开渠道即最短,试说明设计的依据是: .
12. 如图,要把池中的水引到 处,且使所开渠道最短,可过 点作 于 ,然后沿所作的线段 开渠,所开渠道即最短,试说明设计的依据是: . 13. 若点P(2﹣m,3m+1)在y轴上,则点P的坐标是 .14. 若(a﹣3)2+ =0,则a+b= .15. 如图,把图①中的长方形分成B、C两部分,恰与正方形A拼接成如图②的大正方形.如果正方形A的面积为2,拼接后的大正方形的面积是5,则图①中原长方形的长和宽分别是 , .
13. 若点P(2﹣m,3m+1)在y轴上,则点P的坐标是 .14. 若(a﹣3)2+ =0,则a+b= .15. 如图,把图①中的长方形分成B、C两部分,恰与正方形A拼接成如图②的大正方形.如果正方形A的面积为2,拼接后的大正方形的面积是5,则图①中原长方形的长和宽分别是 , . 16. 如图,在平面直角坐标系下xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,3),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为3时,m=;当点B的横坐标为3n(n为正整数)时,m= . (用含n的代数式表示)
16. 如图,在平面直角坐标系下xOy中,我们把横、纵坐标都是整数的点叫做整点.已知点A(0,3),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m.当点B的横坐标为3时,m=;当点B的横坐标为3n(n为正整数)时,m= . (用含n的代数式表示)
三、解答题(本题共68分,第17-22题,每小题5分,第23-25题,每小题5分,第26题,7分,第27题,6分,第28题,7分)解答应写出文字说明,演算步骤或证明过程。
-
17. 计算:22+|﹣ |﹣ +(﹣1)3 .18.
计算: ﹣ .
19. 计算:| -1|﹣| -2|+| - |.20. 已知(x﹣1)2=4,求x的值.21. 如图,点A在∠O的一边上,按要求画图并填空. (1)、①过点A画直线AB⊥OA于点A,与∠O的另一边相交于点B.
(1)、①过点A画直线AB⊥OA于点A,与∠O的另一边相交于点B.
②过点A画OB的垂线段AC,垂足为点C.
③过点C画直线CD∥OA,交直线AB于点D.(2)、∠CDB=°;(3)、如果OA=8,AB=6,AC= ,则点A到直线OB的距离为 .22. 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,﹣2),B(3,﹣1),C(2,1).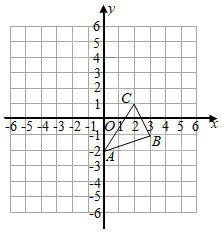 (1)、请在图中画出△ABC向左平移5个单位长度的图形△A'B'C';(2)、写出点A',B',C'的坐标.23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1).
(1)、请在图中画出△ABC向左平移5个单位长度的图形△A'B'C';(2)、写出点A',B',C'的坐标.23. 如图,是小明所在学校的平面示意图,已知宿舍楼的位置是(3,4),艺术楼的位置是(﹣3,1). (1)、根据题意,画出相应的平面直角坐标系;(2)、分别写出教学楼、体育馆的位置;(3)、若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.24. 完成下面的证明,
(1)、根据题意,画出相应的平面直角坐标系;(2)、分别写出教学楼、体育馆的位置;(3)、若学校行政楼的位置是(﹣1,﹣1),在图中标出行政楼的位置.24. 完成下面的证明,如图,AD∥BE,∠1=∠2,求证:∠A=∠E.
证明:∵AD∥BE(已知),
∴∠A= ( ).
∵∠1=∠2(已知),
∴DE∥ ( ).
∴∠E= ( ).
∴∠A=∠E(等量代换).
 25. 如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连接OF.
25. 如图,点O在直线AB上,OC⊥OD,∠D与∠1互余,F是DE上一点,连接OF.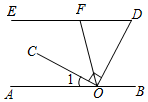 (1)、求证:ED∥AB.(2)、若OF平分∠COD,∠OFD=70°,求∠1的度数.26. 在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
(1)、求证:ED∥AB.(2)、若OF平分∠COD,∠OFD=70°,求∠1的度数.26. 在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
 (1)、直接写出线段AC与线段DE的位置关系;(2)、在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
(1)、直接写出线段AC与线段DE的位置关系;(2)、在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
27. 在四边形ABCD中,∠BAD=∠BCD,AB∥DC,点E是射线CD上一个动点(不与C,D重合),过点E作EF∥AD,交直线AC于点F. (1)、如图,当点E在线段CD上时,求证:∠DEF=∠DCB.(2)、若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .28. 在平面直角坐标系xOy中,点A的坐标为(1,2)、B(1,b).给出如下定义:若△ABC是以AB为腰的等腰直角三角形,就称点C为线段AB的“伴随顶点”.
(1)、如图,当点E在线段CD上时,求证:∠DEF=∠DCB.(2)、若点E在线段CD的延长线上,用等式表示∠DEF与∠DCB之间的数量关系是 .28. 在平面直角坐标系xOy中,点A的坐标为(1,2)、B(1,b).给出如下定义:若△ABC是以AB为腰的等腰直角三角形,就称点C为线段AB的“伴随顶点”. (1)、若b=5,点C是第一象限的点,则线段AB的伴随顶点C的坐标是 .(2)、若△ABC的面积等于8时,求线段AB的伴随顶点C的坐标.
(1)、若b=5,点C是第一象限的点,则线段AB的伴随顶点C的坐标是 .(2)、若△ABC的面积等于8时,求线段AB的伴随顶点C的坐标.