云南省曲靖市罗平县2021年中考数学二模试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 据统计,新冠病毒全球感染总数突破1亿3000万人,死亡超过300万人,其中1亿3000万用科学记数法可表示为( )A、 B、 C、 D、2. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列4个数中,是负数的是( )A、 B、 C、 D、4. 现有4条线段,长度依次是2、5、7、8,从中任选三条,能组成三角形的概率是( )A、 B、 C、 D、5. 一个正多边形的一个内角是 ,则这个正多边形是( )A、十边形 B、九边形 C、八边形 D、七边形6. 数学是研究化学的重要工具,数学知识广泛应用于化学邻域,比如在学习化学的醇类化学式中,甲醇化学式为 ,乙醇化学式为 ,丙醇化学式为 ……,设碳原子的数目为n(n为正整数),则醇类的化学式可以用下列哪个式子来表示( )A、 B、 C、 D、7. 一个空间几何体的主视图和左视图都是边长为 的正三角形,俯视图是一个圆,那么这个几何体的表面积是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是( )
3. 下列4个数中,是负数的是( )A、 B、 C、 D、4. 现有4条线段,长度依次是2、5、7、8,从中任选三条,能组成三角形的概率是( )A、 B、 C、 D、5. 一个正多边形的一个内角是 ,则这个正多边形是( )A、十边形 B、九边形 C、八边形 D、七边形6. 数学是研究化学的重要工具,数学知识广泛应用于化学邻域,比如在学习化学的醇类化学式中,甲醇化学式为 ,乙醇化学式为 ,丙醇化学式为 ……,设碳原子的数目为n(n为正整数),则醇类的化学式可以用下列哪个式子来表示( )A、 B、 C、 D、7. 一个空间几何体的主视图和左视图都是边长为 的正三角形,俯视图是一个圆,那么这个几何体的表面积是( )A、 B、 C、 D、8. 如图,在平面直角坐标系中,直线l为正比例函数 的图象,点 的坐标为 ,过点 作x轴的垂线交直线 于点 ,以 为边作正方形 ;过点 作直线l的垂线,垂足为 ,交x轴于点 ,以 为边作正方形 ;过点 作x轴的垂线,垂足为 ,交直线 于点 ,以 为边作正方形 ,…,按此规律操作下所得到的正方形 的面积是( )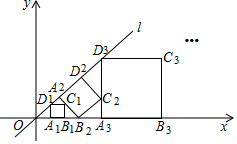 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 使代数式 有意义的 的取值范围是 .10. 因式分解: .11. 已知, ,则 的值为 .12. 如图,四边形ABCD是矩形,BC=2AB,A,B两点的坐标分别是(﹣1,0),(0,1),C,D两点在反比例函数y= (x<0)的图象上,则k的值是.
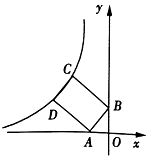 13. 如图, 中, , , ,将 绕点C顺时针旋转,点A,B的对应点分别为 、 ,当点恰好落在线段 上时,弧 与线段 、 围成的阴影部分的面积为 .
13. 如图, 中, , , ,将 绕点C顺时针旋转,点A,B的对应点分别为 、 ,当点恰好落在线段 上时,弧 与线段 、 围成的阴影部分的面积为 . 14. 在半径长为 的圆中,圆内接 的边 长为 ,则 的度数为 .
14. 在半径长为 的圆中,圆内接 的边 长为 ,则 的度数为 .三、解答题
-
15. 先化简,再求值: ,请从不等式组 的整数解中选择一个合适的值代入求值.16. 如图, , , ,且 ,求证: .
 17. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”.为了让同学们理解这次活动的重要性,珍惜粮食.校学生会在某天午餐后,随机抽查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制了如图所示不完整的统计图.
17. 某校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”.为了让同学们理解这次活动的重要性,珍惜粮食.校学生会在某天午餐后,随机抽查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制了如图所示不完整的统计图.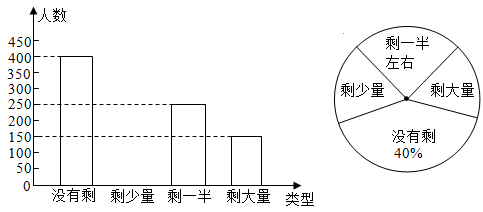 (1)、本次抽样调查的样本容量为人,“剩一半左右”所占圆心角的度数为;(2)、把条形统计图补充完整;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供100人用一餐.据此估算,该校15000名学生一餐浪费的食物可以供多少人食用一餐?18. 我校要进行理化实验操作考试,需用八年级两个班级的学生整理实验器材.已知一班单独整理需要 分钟完成.如果一班与二班共同整理 分钟后,一班另有任务需要离开,剩余工作由二班单独整理 分钟才完成任务,求二班单独整理这批实验器材需要多少分钟?19. 为加深对“创建为民、创建惠民”省级文明城市宗旨的了解,某中学组织学生玩抽卡片的游戏.游戏规则如下:
(1)、本次抽样调查的样本容量为人,“剩一半左右”所占圆心角的度数为;(2)、把条形统计图补充完整;(3)、校学生会通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供100人用一餐.据此估算,该校15000名学生一餐浪费的食物可以供多少人食用一餐?18. 我校要进行理化实验操作考试,需用八年级两个班级的学生整理实验器材.已知一班单独整理需要 分钟完成.如果一班与二班共同整理 分钟后,一班另有任务需要离开,剩余工作由二班单独整理 分钟才完成任务,求二班单独整理这批实验器材需要多少分钟?19. 为加深对“创建为民、创建惠民”省级文明城市宗旨的了解,某中学组织学生玩抽卡片的游戏.游戏规则如下:a.四张卡片(形状、大小和质地都相同),正面分别写有“创建”“为民”“创建”“惠民”;
b.将这四张卡片背面朝上洗匀,从中随机抽取一张(不放回),接着再随机抽取一张;
c.若抽取的两张卡片能组成“创建为民”或“创建惠民”,则获得一次成为“文明倡导者”的机会.
 (1)、第一次抽取的卡片上写的是“创建”的概率为.(2)、求欢欢抽取完两张卡片后,能获得成为“文明倡导者”机会的概率.20. 如图,在平面直角坐标系中,抛物线与x轴交于点 , ,与y轴交于点C,直线 的解析式为 .
(1)、第一次抽取的卡片上写的是“创建”的概率为.(2)、求欢欢抽取完两张卡片后,能获得成为“文明倡导者”机会的概率.20. 如图,在平面直角坐标系中,抛物线与x轴交于点 , ,与y轴交于点C,直线 的解析式为 . (1)、求直线 的解析式和抛物线的解析式;(2)、点 在平面直角坐标系第一象限内的抛物线上运动,设 的面积为S,求S关于m的函数表达式和S的最大值,并指出m的取值范围.21. 如图, 是 的直径,C为 上一点,作 于点E, ,延长 至点D,使得 ,P是弧 (异于 , )上一个动点,连接 , , , , .
(1)、求直线 的解析式和抛物线的解析式;(2)、点 在平面直角坐标系第一象限内的抛物线上运动,设 的面积为S,求S关于m的函数表达式和S的最大值,并指出m的取值范围.21. 如图, 是 的直径,C为 上一点,作 于点E, ,延长 至点D,使得 ,P是弧 (异于 , )上一个动点,连接 , , , , . (1)、求证: 是 的切线;(2)、若 ,求 的长度.22. 某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量m(单位:件)是关于时间t(单位:天)的一次函数,调研所获的部分数据如下表:
(1)、求证: 是 的切线;(2)、若 ,求 的长度.22. 某产品每件成本为20元,经过市场调研发现,这种产品在未来20天内的日销售量m(单位:件)是关于时间t(单位:天)的一次函数,调研所获的部分数据如下表:时间t/天
1
3
10
20
日销售量m/件
98
94
80
60
这20天中,该产品每天的价格y(单位:元/件)与时间t的函数关系式为: (t为整数),根据以上提供的条件解决下列问题:
(1)、直接写出m关于t的函数关系式;(2)、这20天中哪一天的日销售利润最大,最大的销售利润是多少?(3)、在实际销售的20天中,每销售一件商品就捐赠a元( )给希望工程,通过销售记录发现,这20天中,每天扣除捐赠后的日销利润随时间t的增大而增大,求a的取值范围.23.
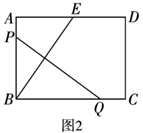
 (1)、如图1,矩形 中,点P、Q分别在线段 、 上,点B与点E关于 对称,点E在线段 上,连接 、 、 交 于点O.求证:四边形 是菱形;(2)、如图2,矩形 中, ,点P、Q分别在线段 、 上,点B与点E关于 对称,点E在线段 上, ,求 的长;(3)、如图3,有一块矩形空地 , , ,点P是一个休息站且在线段 上, ,点Q在线段 上,现要在点B关于 对称的点E处修建一口水井,并且修建水渠 和 ,以便于在四边形空地 上种植花草,余下部分贴上地砖.种植花草的四边形空地 的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.
(1)、如图1,矩形 中,点P、Q分别在线段 、 上,点B与点E关于 对称,点E在线段 上,连接 、 、 交 于点O.求证:四边形 是菱形;(2)、如图2,矩形 中, ,点P、Q分别在线段 、 上,点B与点E关于 对称,点E在线段 上, ,求 的长;(3)、如图3,有一块矩形空地 , , ,点P是一个休息站且在线段 上, ,点Q在线段 上,现要在点B关于 对称的点E处修建一口水井,并且修建水渠 和 ,以便于在四边形空地 上种植花草,余下部分贴上地砖.种植花草的四边形空地 的面积是否存在最小值,若存在,请求出最小值,若不存在,请说明理由.