云南省昆明市官渡区2021年中考数学一模试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 2021 B、﹣2021 C、 D、±20212. 数学无处不在,如图是一个螺栓的示意图,它的俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、“任意画一个三角形,内角和为 ”为必然事件 C、可能性是 的事件在一次试验中一定不会发生 D、抛掷一枚质地均匀的硬币,前两次都是正面朝上,则第3次一定正面朝上4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线 ,直线c与直线a,b分别交于A,B两点, 于点A,交直线b于点C,如果 ,那么 的度数为( )
3. 下列说法正确的是( )A、检测某批次灯泡的使用寿命,适宜用全面调查 B、“任意画一个三角形,内角和为 ”为必然事件 C、可能性是 的事件在一次试验中一定不会发生 D、抛掷一枚质地均匀的硬币,前两次都是正面朝上,则第3次一定正面朝上4. 下列计算正确的是( )A、 B、 C、 D、5. 如图,直线 ,直线c与直线a,b分别交于A,B两点, 于点A,交直线b于点C,如果 ,那么 的度数为( ) A、 B、 C、 D、6. 如图,阴影部分是由3个小正方形组成的一个图形,若在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( )
A、 B、 C、 D、6. 如图,阴影部分是由3个小正方形组成的一个图形,若在图中剩余的方格中涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( ) A、2种 B、3种 C、4种 D、5种7. 学校研究性学习小组的同学测量旗杆的高度.如图,在教学楼一楼地面C处测得旗杆顶部的仰角为 ,在教学楼三楼地面D处测得旗杆顶部的仰角为 ,旗杆底部与教学楼一楼在同一水平线上,已知教学楼每层楼的高度约为3.3米,则旗杆 的高度最接近( )
A、2种 B、3种 C、4种 D、5种7. 学校研究性学习小组的同学测量旗杆的高度.如图,在教学楼一楼地面C处测得旗杆顶部的仰角为 ,在教学楼三楼地面D处测得旗杆顶部的仰角为 ,旗杆底部与教学楼一楼在同一水平线上,已知教学楼每层楼的高度约为3.3米,则旗杆 的高度最接近( )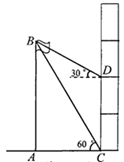 A、8米 B、9米 C、10米 D、11米8. 莱洛三角形,也译作勒洛三角形或圆弧三角形,它的应用广泛,不仅用于建筑、商品的外包装设计,还用在工业方面.莱洛三角形形状的钻头可钻出正方形的孔,发动机的原件上也有莱洛三角形,如图1.别以等边 的顶点A,B,C为圆心,以 长为半径画弧,我们把这三条弧组成的封闭图形就叫做莱洛三角形,如图2.若 ,则莱洛三角形的面积(即阴影部分面积)为( )
A、8米 B、9米 C、10米 D、11米8. 莱洛三角形,也译作勒洛三角形或圆弧三角形,它的应用广泛,不仅用于建筑、商品的外包装设计,还用在工业方面.莱洛三角形形状的钻头可钻出正方形的孔,发动机的原件上也有莱洛三角形,如图1.别以等边 的顶点A,B,C为圆心,以 长为半径画弧,我们把这三条弧组成的封闭图形就叫做莱洛三角形,如图2.若 ,则莱洛三角形的面积(即阴影部分面积)为( )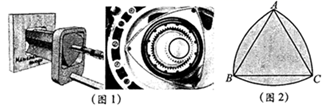 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
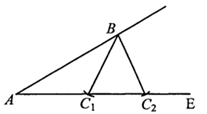
9. 函数 中,自变量x的取值范围是 .10. 云南自贸试验区的实施范围涵盖了昆明、红河、德宏三个片区,其中昆明片区760000平方千米,占总量的 .将760000这个数用科学记数法可表示为 .11. 因式分解:x3-9x=.12. 如果一个多边形的每一个外角都等于72°,则该多边形的内角和等于 .13. 观察下列关于x的单项式, , , , , , ,按照上述规律,第2021个单项式是 .14. 我们知道,给出两边及其中一边的对角的三角形不一定是唯一的.例如 中, , , ,我们可以作 ,截取 ,以B为圆心,6为半径作弧,与射线 交于点 , ,则 和 均为满足条件的三角形.已知,平行四边形 中, , , 边上的高为12,则平行四边形 面积为 .
三、解答题
-
15. 计算:( )﹣2﹣(π﹣ )0+| ﹣2|+4tan60°.16. 风筝起源于中国,至今已有2300多年的历史.如图,在小明设计的“风筝”图案中,已知 , , .求证: .
 17. 近年来网约车给人们的出行带来了便利.初三的王冬和数学兴趣小组的同学对“美团”和“滴滴”两家网约车公司司机月收入进行了一项抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
17. 近年来网约车给人们的出行带来了便利.初三的王冬和数学兴趣小组的同学对“美团”和“滴滴”两家网约车公司司机月收入进行了一项抽样调查,两家公司分别抽取的10名司机月收入(单位:千元)如图所示:
根据以上信息,整理分析数据如下:
平均月收入
中位数
众数
方差
“美团”
a
6
c
1.2
“滴滴”
6
b
4
7.6
(1)、填空: ; ; ;(2)、王冬的叔叔决定从两家公司中选择一家做网约车司机,如果你是王冬,你建议他选哪家公司?说明理由.18. 某游乐园采用手机APP购票,智能闸机验票的方式,大大缩短了游客排队购票、验票的等待时间,平均每分钟接待游客的人数是原来的10倍,且接待5000名游客的入园时间比原来接待600名游客的入园时间还少5分钟,求游乐园原来平均每分钟接待游客的人数.19. 四张正面分别写有数字:-2,-1,0,1的卡片,它们的背面完全相同,现将这四张卡片背面朝上洗匀.(1)、从中任意抽取一张卡片,则所抽卡片上数字为负数的概率是;(2)、先从中任意抽取一张卡片,以其正面数字作为x的值,然后再从剩余的卡片中随机抽一张,以其正面的数字作为y的值,请用列表法或树状图法,求点 在第二象限的概率.20. 如图,在矩形 的 边上取一点E,连接 ,使得 ,在 边上取一点F,使得 ,连接 ,过点D作 于G.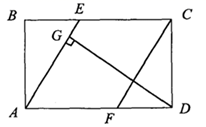 (1)、求证:四边形 是菱形;(2)、若 , ,求 的长.21. 某品牌热水器中原有水的温度为20℃,开机通电,热水器启动开始加热(此过程中水温y℃与开机时间x分钟满足一次函数关系),当加热到70℃时自动停止加热,随后水温开始下降(此时水温y℃与开机时间x分钟成反比例函数关系).当水温降至35℃时,热水器又自动以相同的功率加热至70℃,…,重复上述过程.如图,根据图象提供的信息,解答下列问题:
(1)、求证:四边形 是菱形;(2)、若 , ,求 的长.21. 某品牌热水器中原有水的温度为20℃,开机通电,热水器启动开始加热(此过程中水温y℃与开机时间x分钟满足一次函数关系),当加热到70℃时自动停止加热,随后水温开始下降(此时水温y℃与开机时间x分钟成反比例函数关系).当水温降至35℃时,热水器又自动以相同的功率加热至70℃,…,重复上述过程.如图,根据图象提供的信息,解答下列问题: (1)、当0≤x≤25时,求水温y℃开机时间x分钟的函数表达式;(2)、求图中t的值;(3)、开机通电60分钟时,热水器中水的温度y约为多少摄氏度?
(1)、当0≤x≤25时,求水温y℃开机时间x分钟的函数表达式;(2)、求图中t的值;(3)、开机通电60分钟时,热水器中水的温度y约为多少摄氏度?

