浙江省丽水市2021年中考数学试卷
试卷更新日期：2021-06-17 类型：中考真卷
一、选择题（本题有10小题，每小题3分，共30分）
-
1. 实数﹣2的倒数是（ ）A、2 B、﹣2 C、 D、﹣2. 计算（﹣a）2•a4的结果是（ ）A、a6 B、﹣a6 C、a8 D、﹣a83. 如图是由5个相同的小立方体搭成的几何体，它的主视图是（ ）
A、
B、
C、
D、
4. 一个布袋里装有3个红球和5个黄球，它们除颜色外其余都相同从中任意摸出一个球是红球的概率是（ ）A、 B、 C、 D、5. 若﹣3a＞1，两边都除以﹣3，得（ ）A、a＜﹣ B、a＞﹣ C、a＜﹣3 D、a＞﹣36. 用配方法解方程x2+4x+1＝0时，配方结果正确的是（ ）A、（x﹣2）2＝5 B、（x﹣2） 2＝3 C、（x+2） 2＝5 D、（x+2） 2＝37. 如图，AB是⊙O的直径，弦CD⊥OA于点E，连结OC，OD．若⊙O的半径为m，∠AOD＝∠α，则下列结论一定成立的是（ ）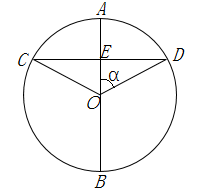
A、oE＝m•tanα B、CD＝2m•sinα C、AE＝m•cosα D、S△COD＝m2•sinα8. 四盏灯笼的位置如图．已知A ， B ， C ， D的坐标分别是（﹣1，b），（1，b），（2，b），（3，5，b），平移y轴右侧的一盏灯笼，使得y轴两侧的灯笼对称，则平移的方法可以是（ ）
A、将B向左平移4.5个单位 B、将C向左平移4个单位 C、将D向左平移5.5个单位 D、将C向左平移3.5个单位9. 一杠杆装置如图，杆的一端吊起一桶水，水桶对杆的拉力的作用点到支点的杆长固定不变．甲、乙、丙、丁四位同学分别在杆的另一端竖直向下施加压力F甲、F乙、F丙、F丁 ， 将相同重量的水桶吊起同样的高度，若F乙＜F丙＜F甲＜F丁 ， 则这四位同学对杆的压力的作用点到支点的距离最远的是（ ）
A、甲同学 B、乙同学 C、丙同学 D、丁同学10. 如图，在Rt△ABC纸片中，∠ACB＝90°，AC＝4，BC＝3，点D ， E分别在AB ， AC上，连结DE ， 将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上，若FD平分∠EFB ， 则AD的长为（ ）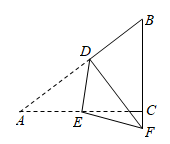
A、 B、 C、 D、二、填空题（本题有6小题，每小题4分，共24分）
-
11. 分解因式：x2﹣4= ．
12. 要使式子 有意义，则x可取的一个数是 ．13. 根据第七次全国人口普查，华东A，B，C，D，E，F六省60岁及以上人口占比情况如图所示，这六省60岁及以上人口占比的中位数是 ．
14. 一个多边形过顶点剪去一个角后，所得多边形的内角和为720°，则原多边形的边数是 ．15. 小丽在“红色研学”活动中深受革命先烈事迹的鼓舞，用正方形纸片制作成图1的七巧板，设计拼成图2的“奔跑者”形象来激励自己．已知图1正方形纸片的边长为4，图2中FM＝2EM，则“奔跑者”两脚之间的跨度，即AB，CD之间的距离是 ．
16. 数学活动课上，小云和小王在讨论张老师出示的一道代数式求值问题：已知实数a，b同时满足a2+2a＝b+2，b2+2b＝a+2，求代数式 的值．
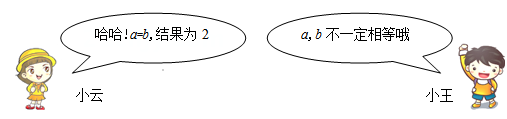
结合他们的对话，请解答下列问题：(1)、当a＝b时，a的值是 ．(2)、当a≠b时，代数式 的值是 ．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分，各小题都必须写出解答过程）
-
17. 计算：|﹣2021|+（﹣3）0﹣ ．18. 解方程组： ．19. 在创建“浙江省健康促进学校”的过程中，某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查，并按照国家分类标准统计人数，绘制成如下两幅不完整的统计图表，请根据图信息解答下列问题：
抽取的学生视力情况统计表
类别
检查结果
人数
A
正常
88
B
轻度近视
C
中度近视
59
D
重度近视
(1)、求所抽取的学生总人数；(2)、该校共有学生约1800人，请估算该校学生中，近视程度为中度和重度的总人数；(3)、请结合上述统计数据，为该校做好近视防控，促进学生健康发展提出一条合理的建议．20. 如图，在5×5的方格纸中，线段AB的端点均在格点上，请按要求画图．
(1)、如图1，画出一条线段AC ， 使AC＝AB ， C在格点上；(2)、如图2，画出一条线段EF ， 使EF ， AB互相平分，E ， F均在格点上；(3)、如图3，以A ， B为顶点画出一个四边形，使其是中心对称图形，且顶点均在格点上．21. 李师傅将容量为60升的货车油箱加满后，从工厂出发运送一批物资到某地．行驶过程中，货车离目的地的路程s（千米）与行驶时间t（小时）的关系如图所示（中途休息、加油的时间不计．当油箱中剩余油量为10升时，货车会自动显示加油提醒．设货车平均耗油量为0.1升/千米，请根据图象解答下列问题：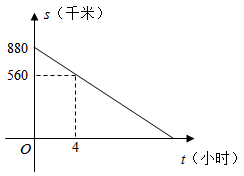
(1)、直接写出工厂离目的地的路程；(2)、求s关于t的函数表达式；(3)、当货车显示加油提醒后，问行驶时间t在怎样的范围内货车应进站加油？22. 如图，在△ABC中，AC＝BC ， 以BC为直径的半圆O交AB于点D ， 过点D作半圆O的切线，交AC于点E ．
(1)、求证：∠ACB＝2∠ADE；(2)、若DE＝3，AE＝ ，求 的长．23. 如图，已知抛物线L：y＝x2+bx+c经过点A（0，﹣5），B（5，0）．
(1)、求b ， c的值；(2)、连结AB ， 交抛物线L的对称轴于点M ．①求点M的坐标；
②将抛物线L向左平移m（m＞0）个单位得到抛物线L1.过点M作MN∥y轴，交抛物线L1于点N ． P是抛物线L1上一点，横坐标为﹣1，过点P作PE∥x轴，交抛物线L于点E ， 点E在抛物线L对称轴的右侧．若PE+MN＝10，求m的值．
24. 如图，在菱形ABCD中，∠ABC是锐角，E是BC边上的动点，将射线AE绕点A按逆时针方向旋转，交直线CD于点F ．
(1)、当AE⊥BC ， ∠EAF＝∠ABC时，①求证：AE＝AF；
②连结BD ， EF ， 若 ，求 的值；
(2)、当∠EAF＝ ∠BAD时，延长BC交射线AF于点M ， 延长DC交射线AE于点N ， 连结AC ， MN ， 若AB＝4，AC＝2，则当CE为何值时，△AMN是等腰三角形．