云南省红河州元阳县2021年中考数学一模试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 经过全党全国各族人民共同努力,在迎来中国共产党成立一百周年的重要时刻,我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,将数据9899万用科学记数法表示为( )A、 B、 C、 D、2. 如图,一个由圆柱和长方体组成的几何体水平放置,它的主视图是( )
 A、
A、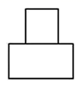 B、
B、 C、
C、 D、
D、 3. 下面计算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、海底捞月是必然事件 B、明天的降水概率为80%,则明天80%的时间下雨,20%的时间不下雨 C、为了调查某校学生的视力情况,在全校的1000名学生中随机抽取了80名学生,其中80名学生是总体的一个样本 D、甲、乙两人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , ,则乙的射击成绩比甲稳定5. 如图,点E是正方形 的边 上的一点,且 ,延长 交 的延长线于点F , 则 和四边形 的面积比为( )
3. 下面计算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、海底捞月是必然事件 B、明天的降水概率为80%,则明天80%的时间下雨,20%的时间不下雨 C、为了调查某校学生的视力情况,在全校的1000名学生中随机抽取了80名学生,其中80名学生是总体的一个样本 D、甲、乙两人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , ,则乙的射击成绩比甲稳定5. 如图,点E是正方形 的边 上的一点,且 ,延长 交 的延长线于点F , 则 和四边形 的面积比为( ) A、 B、 C、 D、6. 按一定规律排列的单项式: ,…第n个单项式是( )A、 B、 C、 D、7. 如图,从一块半径为 的圆形铁皮上剪出一个圆心角是 的扇形 ,则此扇形围成的圆锥底面圆的半径为( )
A、 B、 C、 D、6. 按一定规律排列的单项式: ,…第n个单项式是( )A、 B、 C、 D、7. 如图,从一块半径为 的圆形铁皮上剪出一个圆心角是 的扇形 ,则此扇形围成的圆锥底面圆的半径为( ) A、 B、 C、 D、8. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 有正数解,则所有满足条件的整数a的值为( )A、6,7,8,9 B、6,7,8 C、7,8 D、6,8
A、 B、 C、 D、8. 若关于x的一元一次不等式组 的解集为 ,且关于y的分式方程 有正数解,则所有满足条件的整数a的值为( )A、6,7,8,9 B、6,7,8 C、7,8 D、6,8二、填空题
-
9. 若一个数的相反数是-7,则这个数为 .10. 如图,将直尺与三角尺叠放在一起,如果 ,那么 的度数为 .
 11. 若使代数式 有意义,则x的取值范围是 .12. 已知关于x的反比例函数 经过点 ,则b= .13. 若关于x的一元二次方程 有两个相等的实数根,则 .14. 如图,菱形 的周长为8厘米, ,点M为 的中点,点N是边 上任一点,把 沿直线 折叠,点A落在图中的点E处,当 厘米时, 是直角三角形.
11. 若使代数式 有意义,则x的取值范围是 .12. 已知关于x的反比例函数 经过点 ,则b= .13. 若关于x的一元二次方程 有两个相等的实数根,则 .14. 如图,菱形 的周长为8厘米, ,点M为 的中点,点N是边 上任一点,把 沿直线 折叠,点A落在图中的点E处,当 厘米时, 是直角三角形.
三、解答题
-
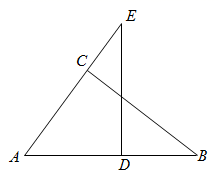
15. 先化简,再求值: ,其中 .16. 如图,已知 ,求证: .
 17. 某校女子排球队10名队员的身高(单位: )如下:170、175、165、185、175、170、175、170、165、170(1)、该校10名队员身高的中位数为 , 众数为;(2)、求该校10名队员身高的平均数;(3)、在一次训练中,一名队员受伤暂时退出训练了,此时该校9名排球队队员的平均身高提高了,则受伤队员的身高可能是cm.18. 大理以其秀丽的自然风光、丰富的文物古迹、浓厚的民族风情深深吸引了无数中外游客王华和李强同住一个小区,假期相约一起去大理游玩已知从他们小区到大理的乘车距离约为 ,王华乘大巴车出发5小时后,李强开轿车自驾游,最后他们同时到达目的地.已知轿车的速度是大巴车速度的2倍.求轿车的速度.19. 将4张印有我国传统节日“春节”“元宵节”“清明节”“中秋节”(卡片的形状、大小、质地都相同)的卡片放在一个不透明的盒子中,将卡片搅匀.(1)、从盒子中任意取出1张卡片,恰好取出印有“春节”的卡片的概率为 .(2)、先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的2张卡片中,印有相同节日的概率(请用画树状图法或列表法求解).20. 如图,以 的边 为直径作 ,交 于点D , D为 的中点,过点D作 ,垂足为E .
17. 某校女子排球队10名队员的身高(单位: )如下:170、175、165、185、175、170、175、170、165、170(1)、该校10名队员身高的中位数为 , 众数为;(2)、求该校10名队员身高的平均数;(3)、在一次训练中,一名队员受伤暂时退出训练了,此时该校9名排球队队员的平均身高提高了,则受伤队员的身高可能是cm.18. 大理以其秀丽的自然风光、丰富的文物古迹、浓厚的民族风情深深吸引了无数中外游客王华和李强同住一个小区,假期相约一起去大理游玩已知从他们小区到大理的乘车距离约为 ,王华乘大巴车出发5小时后,李强开轿车自驾游,最后他们同时到达目的地.已知轿车的速度是大巴车速度的2倍.求轿车的速度.19. 将4张印有我国传统节日“春节”“元宵节”“清明节”“中秋节”(卡片的形状、大小、质地都相同)的卡片放在一个不透明的盒子中,将卡片搅匀.(1)、从盒子中任意取出1张卡片,恰好取出印有“春节”的卡片的概率为 .(2)、先从盒子中任意取出1张卡片,记录后放回并搅匀,再从中任意取出1张卡片,求取出的2张卡片中,印有相同节日的概率(请用画树状图法或列表法求解).20. 如图,以 的边 为直径作 ,交 于点D , D为 的中点,过点D作 ,垂足为E .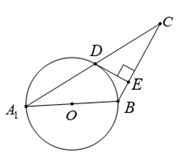 (1)、证明: 是 的切线.(2)、若 的半径为5, ,求 的长.21. 在抗击疫情期间,某社区准备购买酒精和消毒液两种消毒物资供居民使用.第一次购买酒精20瓶,消毒液20瓶,共花费300元;第二次购买酒精15瓶,消毒液40瓶,共花费350元.(1)、分别求出每瓶酒精和消毒液的价格;(2)、若要购买60瓶这两种消毒物资,设购买酒精x瓶,这两种消毒物资的总费用为y元,求y与x的函数解析式;(3)、在(2)的条件下,若要求购买酒精的数量不少于消毒液数量的2倍,求总费用y的最小值.
(1)、证明: 是 的切线.(2)、若 的半径为5, ,求 的长.21. 在抗击疫情期间,某社区准备购买酒精和消毒液两种消毒物资供居民使用.第一次购买酒精20瓶,消毒液20瓶,共花费300元;第二次购买酒精15瓶,消毒液40瓶,共花费350元.(1)、分别求出每瓶酒精和消毒液的价格;(2)、若要购买60瓶这两种消毒物资,设购买酒精x瓶,这两种消毒物资的总费用为y元,求y与x的函数解析式;(3)、在(2)的条件下,若要求购买酒精的数量不少于消毒液数量的2倍,求总费用y的最小值.