云南省大理2021年中考数学二模试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 若分式 有意义,则( )A、 B、 C、 D、 且2. 2020年4月7日,中国邮政发行了《众志成城 抗击疫情》邮票一套两枚(图1),以此纪念在抗击新冠肺炎疫情的过程中,中国人民所展现出的“中国精神、中国力量、中国担当”.两枚邮票用一个“众”字型的背景图案巧妙相连,从几何的角度看,这个图案(图2)( )
 A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形3. 一个n边形的每个外角都是45°,则这个n边形的内角和是( )A、1080° B、540° C、2700° D、2160°4. 不等式组 中,不等式①和②的解集在数轴上表示正确的是( )A、
A、是中心对称图形而不是轴对称图形 B、是轴对称图形而不是中心对称图形 C、既是轴对称图形又是中心对称图形 D、既不是轴对称图形,又不是中心对称图形3. 一个n边形的每个外角都是45°,则这个n边形的内角和是( )A、1080° B、540° C、2700° D、2160°4. 不等式组 中,不等式①和②的解集在数轴上表示正确的是( )A、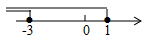 B、
B、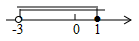 C、
C、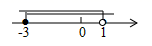 D、
D、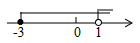 5. 反比例函数 的图象过点 ,则k的值为( )A、15 B、 C、-15 D、6. 某企业为了推选代表队参加市职业技能大赛,对甲、乙两个车间进行了五次测试,其中甲车间五次成绩的平均数是90分,中位数是91分,方差是2.4;乙车间五次成绩的平均数是90分,中位数是89分,方差是4.4.下列说法正确的是( )A、甲车间成绩的平均水平高于乙车间 B、甲、乙两车间成绩一样稳定 C、甲车间成绩优秀的次数少于乙车间(成绩不低于90分为优秀) D、若选派甲车间去参加比赛,取得好成绩的可能性更大7. 已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )A、20πcm2 B、20cm2 C、40πcm2 D、40cm28. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )
5. 反比例函数 的图象过点 ,则k的值为( )A、15 B、 C、-15 D、6. 某企业为了推选代表队参加市职业技能大赛,对甲、乙两个车间进行了五次测试,其中甲车间五次成绩的平均数是90分,中位数是91分,方差是2.4;乙车间五次成绩的平均数是90分,中位数是89分,方差是4.4.下列说法正确的是( )A、甲车间成绩的平均水平高于乙车间 B、甲、乙两车间成绩一样稳定 C、甲车间成绩优秀的次数少于乙车间(成绩不低于90分为优秀) D、若选派甲车间去参加比赛,取得好成绩的可能性更大7. 已知圆锥的底面半径为4cm,母线长为5cm,则这个圆锥的侧面积是( )A、20πcm2 B、20cm2 C、40πcm2 D、40cm28. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给以下结论:①abc<0;②c+2a<0;③9a﹣3b+c=0;④a﹣b≥m(am+b)(m为实数);⑤4ac﹣b2<0.其中错误结论的个数有( )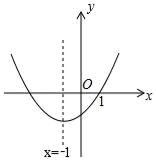 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 小明的姐姐在银行工作,她把存入3万元记作+3万元,那么-1万元表示 .10. 分解因式:3x2-6x+3= .11. 在疫情泛滥期间,口罩已经变成硬通货,其中,N95口罩尤其火爆,N95口罩对直径为0.0000003米(即0.3微米)的颗粒物过滤效果会大于等于95%,N95口罩强大的防护能力在于它的静电纤维吸附能力,0.0000003用科学记数法表示为 .12. 已知:如图,在三角形 中, , 边 上的高, , ,则
 13. 《生物多样性公约》第十五次缔约方大会(COP15)将于2021年10月11日至24日在云南省昆明市举办.昆明某景观园林公司为迎接大会召开,计划在一个长35米、宽20米的矩形场地上要开辟一横两纵三条等宽的小道(如图),其余部分种植草坪,草坪面积为627平方米.设小道的宽为x米,则可列方程为 .
13. 《生物多样性公约》第十五次缔约方大会(COP15)将于2021年10月11日至24日在云南省昆明市举办.昆明某景观园林公司为迎接大会召开,计划在一个长35米、宽20米的矩形场地上要开辟一横两纵三条等宽的小道(如图),其余部分种植草坪,草坪面积为627平方米.设小道的宽为x米,则可列方程为 . 14. 观察下列各组勾股数,并寻找规律:
14. 观察下列各组勾股数,并寻找规律:①4,3,5; ②6,8,10; ③8,15,17; ④10,24,26 ……
请根据你发现的规律写出第⑦组勾股数:.
三、解答题
-
15. 化简求值: ,其中 .16. 我们把两组邻边相等的四边形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.求证OE=OF.
 17. 为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,对其部分文字的笔画数进行统计,结果如下表:
17. 为了了解现行简化汉字的笔画画数情况,某同学随机选取语文课本的一篇文章,对其部分文字的笔画数进行统计,结果如下表:笔画数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
字数
4
8
10
16
14
20
24
36
16
14
11
9
10
7
1
请解答下列问题:
(1)、被统计汉字笔画数的众数是多少?(2)、该同学将数据进行整理,按如下方案分组统计,并制作扇形统计图:分组
笔画数 (画)
字数(个)
A组
22
B组
m
C组
76
D组
n
E组
18
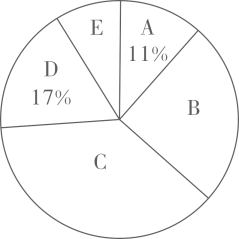
请确定上表中m、n的值及扇形统计图中组对应扇形圆心角的度数.
(3)、若这篇文章共有3500个汉字,估计笔画数在 画( 组)的字数有多少个?18. 某工厂有工人60人,生产某种由一个螺栓套两个螺母的配套产品,每人每天生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,才能使生产出的螺栓和螺母刚好配套?19. 在一个不透明的盒里装有4张除数字外其他完全相同且标号为0,1,2,3的卡片,小明从盒里随机取出一张卡片,记下数字为x,小亮从剩下的3张卡片中随机取出一张卡片,记下数字为y.(1)、用列表法或画树状图法(树状图也称树形图)中的一种方法,写出(x,y)所有可能出现的结果;(2)、求小明摸出的卡片上的数字x大于小亮摸出的卡片上的数字y的概率.20. 如图,正比例函数 的图像与反比例函数 的图像交于点 .点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.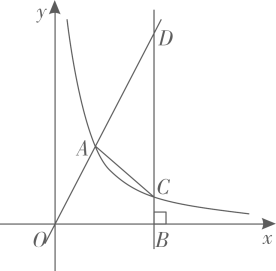 (1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.21. 如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.
(1)、求a的值及正比例函数 的表达式;(2)、若 ,求 的面积.21. 如图,在矩形 ABCD 中,AE 平分∠BAD,交 BC 于 E,过 E 做 EF⊥AD 于 F,连接BF交AE于P,连接PD.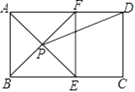 (1)、求证:四边形ABEF 是正方形;(2)、如果AB=6,AD=8,求tan∠ADP的值.22. 在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件, )满足一次函数的关系,部分数据如下表:
(1)、求证:四边形ABEF 是正方形;(2)、如果AB=6,AD=8,求tan∠ADP的值.22. 在“新冠”疫情期间,全国人民“众志成城,同心抗疫”,某商家决定将一个月获得的利润全部捐赠给社区用于抗疫.已知商家购进一批产品,成本为10元/件,拟采取线上和线下两种方式进行销售.调查发现,线下的月销量y(单位:件)与线下售价x(单位:元/件, )满足一次函数的关系,部分数据如下表: (1)、求y与x的函数关系式;(2)、若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.23. 我们定义:如果圆的两条弦互相垂直且相交,那么这两条弦互为“十字弦”,也把其中的一条弦叫做另一条弦的“十字弦”.如图1,已知⊙O的两条弦AB⊥CD,则AB、CD互为“十字弦”,AB是CD的“十字弦”,CD也是AB的“十字弦”.
(1)、求y与x的函数关系式;(2)、若线上售价始终比线下每件便宜2元,且线上的月销量固定为400件.试问:当 为多少时,线上和线下月利润总和达到最大?并求出此时的最大利润.23. 我们定义:如果圆的两条弦互相垂直且相交,那么这两条弦互为“十字弦”,也把其中的一条弦叫做另一条弦的“十字弦”.如图1,已知⊙O的两条弦AB⊥CD,则AB、CD互为“十字弦”,AB是CD的“十字弦”,CD也是AB的“十字弦”. (1)、(概念理解)
(1)、(概念理解)若⊙O的半径为5,一条弦AB =8,则弦AB的“十字弦”CD的最大值为 , 最小值为 .
(2)、如图2,若⊙O的弦CD恰好是⊙O的直径,弦AB与CD相交于H,连接AC,若AC= 12,DH =7,CH =9,求证︰AB、CD互为“十字弦”; (3)、(问题解决)
(3)、(问题解决)如图3,在⊙O中,半径为 ,弦AB与CD相交于H,AB、CD互为“十字弦”且AB=CD, ,则CD的长度 .
