天津市南开区2021年中考数学三模试卷

试卷更新日期：2021-06-17 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算 $(- 9) \times \frac{1}{3}$ 的结果是（）

A、3 B、27 C、 $- 27$ D、 $- 3$

查看试题解析
2. $cos 45^{\circ}$ 的值等于（）

A、 $\frac{\sqrt{3}}{3}$ B、 $\sqrt{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
3. 2021年5月16日晚，大型音乐史诗《东方红》交响合唱音乐会在天津大剧院音乐厅隆重上演．自今年4月，《东方红》大型交响合唱音乐会开启了全国巡演，已深入14个省市19个城市开展巡演近20场，行程达12000多公里．将“12000”用科学记数法表示为（）

A、 $1.2 \times 10^{4}$ B、 $12 \times 10^{4}$ C、 $0.12 \times 10^{5}$ D、 $12 \times 10^{3}$

查看试题解析
4. 下列图形中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如图是由几个相同的正方体搭成的一个几何体，它的俯视图是（）

A、 B、 C、 D、

查看试题解析
6. 估计 $\sqrt{39}$ 的值在（）

A、4和5之间 B、5和6之间 C、6和7之间 D、7和8之间

查看试题解析
7. 二元一次方程组 ${\begin{array}{l} x - 2 y = 3, \\ x + y = 6 \end{array}$ 的解是（）

A、 ${\begin{array}{l} x = 1, \\ y = 5. \end{array}$ B、 ${\begin{array}{l} x = 3, \\ y = 0. \end{array}$ C、 ${\begin{array}{l} x = 4, \\ y = 2. \end{array}$ D、 ${\begin{array}{l} x = 5, \\ y = 1. \end{array}$

查看试题解析
8. 计算 $\frac{x}{x - 1}$ ＋ $\frac{2 x - 1}{1 - x}$ 的结果为（）

A、﹣1 B、1 C、 $\frac{3 x}{x - 1}$ D、 $\frac{x + 1}{x - 1}$

查看试题解析
9. 若点 $(- 2 ， y_{1}) ， (1 ， y_{2}) ， (3 ， y_{3})$ 在反比例函数 $y = \frac{\sqrt{3}}{x}$ 的图象上，则 $y_{1} ， y_{2} ， y_{3}$ 的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{3} < y_{2} < y_{1}$ C、 $y_{2} < y_{1} < y_{3}$ D、 $y_{1} < y_{3} < y_{2}$

查看试题解析
10. 如图，平行四边形ABCO中的顶点O，A，C的坐标分别为（0，0），（2，3），（m，0），则顶点B的坐标为（）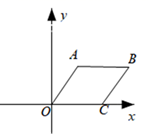

A、（3，2+m） B、（3+m，2） C、（2，3+m） D、（2+m，3）

查看试题解析
11. 如图，在四边形 $A B C D$ 中， $∠ A = ∠ D = 90 ° ， A B = 5 ， A D = 4 ，$ $C D = 3 ，$ 点 $P$ 是边 $A D$ 上的动点，则 $△ P B C$ 周长的最小值为（）

A、 $8$ B、 $4 \sqrt{5}$ C、 $12$ D、 $6 \sqrt{5}$

查看试题解析
12. 抛物线 $y = a x^{2} + b x + c$ 经过点（﹣2，0），且对称轴为直线x=1，其部分图象如图所示．对于此抛物线有如下四个结论：
① $b = 2 a$ ；② $4 a + 2 b + c$ ＞ $0$ ；③若n＞m＞0，则 $x = 1 + m$ 时的函数值小于 $x = 1 - n$ 时的函数值；④点（ $- \frac{c}{2 a}$ ，0）一定在此抛物线上．

其中正确结论的个数是（）

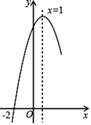A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

13. 计算 $a^{7} \cdot a^{4}$ 的结果是．

查看试题解析
14. 化简 $(3 + 2 \sqrt{2}) (3 - 2 \sqrt{2})$ 的结果为.

查看试题解析
15. 不透明的袋子中有8个球，其中3个红球，2个黄球，3个绿球，除颜色外无差别，从袋子中随机取出1个，则它是黄球的概率是．

查看试题解析
16. 若一次函数 $y = k x + b$ （b为常数）的图象过点 $(5 ， 4)$ ，且与 $y = x$ 的图象平行，这个一次函数的解析式为．

查看试题解析
17. 如图，数轴上有若干个点，每相邻两点相距1个单位长度．其中点A ， B ， C ， D对应的数分别是整数a ， b ， c ， d ，且 $d - 2 a = 12$ ，则 $b + c$ 的值为．

查看试题解析
18. 如图，正方形纸片 $A B C D$ 的边长为5，E是边 $B C$ 的中点，连接 $A E$ ．沿 $A E$ 折叠该纸片，使点B落在F点．则 $C F$ 的长为．

查看试题解析

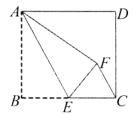
三、解答题

19. 解不等式组组 ${\begin{array}{l} x + 2 > - 1 ， ① \\ 3 x - 1 \leq 2 x ② \end{array}$ ，请结合题意填空，完成本题的解答．

(1)、解不等式①，得﹔

(2)、解不等式②，得﹔

(3)、把不等式①和②的解集在数轴上表示出来：

(4)、原不等式组的解集为．

查看试题解析
20. 根据某校女子排球训练队队员的年龄统计的结果，绘制出了如图的统计图①和图②．

请根据相关信息，解答下列问题：

(1)、训练队的队员人数为人，图①中m的值为；

(2)、求训练队队员年龄数据的平均数、众数和中位数．

查看试题解析
21. 已知⊙O中，AC为直径，MA、MB分别切⊙O于点A、B．

(1)、如图①，若∠BAC=25^° ，求∠AMB的大小；

(2)、如图②，过点B作BD⊥AC于点E，交⊙O于点D，若BD=MA，求∠AMB的大小．

查看试题解析
22. 如图，某办公楼AB的右边有一建筑物CD，在建设物CD离地面2米高的点E处观测办公楼顶A点，测得的仰角 $∠ A E M$ = $22 °$ ，在离建设物CD 25米远的F点观测办公楼顶A点，测得的仰角 $∠ A F B$ = $45 °$ （B，F，C在一条直线上）．

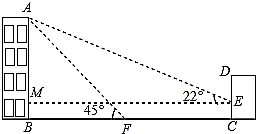(1)、求办公楼AB的高度；

(2)、若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．（参考数据： $\sin 22^{°} = \frac{3}{8} ， \cos 22^{°} = \frac{15}{16} ， \tan 22^{°} = \frac{2}{5}$ ）

查看试题解析
23. 小明骑单车上学，当他骑了一段时间，想起要买某本书，于是又折回到刚经过的新华糖，买到书后继续去学校，根据小明骑车离家的距离 $y (m)$ 与时间 $x (\min)$ 建立平面直角坐标系，根据图中提供的信息回答下列问题：

(1)、小明家到学校的路程是米．

(2)、他折回书店时骑车的速度是米/分，在书店停留了分钟．

(3)、在整个上学的途中分钟至分钟小明骑车速度最快，最快的速度是米/分．

(4)、小明距离家900米时，x= $\min$ ．

(5)、写出整个过程y与x的函数解析式．

查看试题解析