山东省东营市垦利区2021年中考数学二模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、单选题
-
1. 下列图形既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的 ( )A、 B、 C、 D、3. 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )
2. 下列运算正确的 ( )A、 B、 C、 D、3. 将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )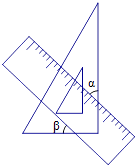 A、43° B、47° C、30° D、60°4. 某物体的三个视图如图所示,该物体的直观图是( )
A、43° B、47° C、30° D、60°4. 某物体的三个视图如图所示,该物体的直观图是( )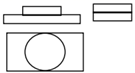 A、
A、 B、
B、 C、
C、 D、
D、 5. 将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点 ,则点 的坐标是( )A、(2,3) B、(2,-1) C、(4,1) D、(0,1)6. 已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示,则一次函数 的图象可能是( )
5. 将抛物线y=x2-4x+5的顶点A向左平移2个单位长度得到点 ,则点 的坐标是( )A、(2,3) B、(2,-1) C、(4,1) D、(0,1)6. 已知在同一直角坐标系中二次函数 和反比例函数 的图象如图所示,则一次函数 的图象可能是( )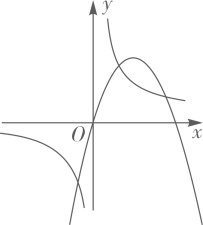 A、
A、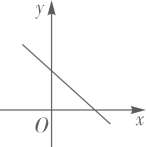 B、
B、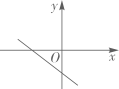 C、
C、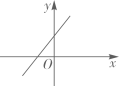 D、
D、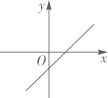 7. 一个圆锥的侧面展开图是半径为6、圆心角为120°的扇形,那么这个圆锥的底面圆的半径为( )A、1 B、2 C、3 D、48. 某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )A、 B、 C、 D、9. 一个盒子里有完全相同的三个小球,球上分别标上数字-2、1、4随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程 有实数根的概率是( )
7. 一个圆锥的侧面展开图是半径为6、圆心角为120°的扇形,那么这个圆锥的底面圆的半径为( )A、1 B、2 C、3 D、48. 某工程队铺设一条480米的景观路,开工后,由于引进先进设备,工作效率比原计划提高50%,结果提前4天完成任务.若设原计划每天铺设x米,根据题意可列方程为( )A、 B、 C、 D、9. 一个盒子里有完全相同的三个小球,球上分别标上数字-2、1、4随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程 有实数根的概率是( )
A、 B、 C、 D、10. 如图,在正方形 中,点P是 上一动点(不与A,B重合),对角线 、 相交于点O,过点P分别作 、 的垂线,分别交 、 于点E、F,交 、 于点M、N、下列结论:① ;② ;③ ;④ ;⑤当 时,点P是 的中点.其中正确的结论有( )个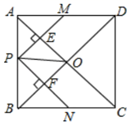 A、5个 B、4个 C、3个 D、2个
A、5个 B、4个 C、3个 D、2个二、填空题
-
11. 国务院总理温家宝在政府工作报告中指出,我国2012年国内生产总值51.9万亿元.51.9万亿元用科学记数法表示为元.12. 分解因式: .13. 某中学足球队9名队员的年龄情况如下:
年龄(单位:岁)
14
15
16
17
人数
1
4
2
2
则该队队员年龄的众数和中位数分别是
14. 如图, 的顶点O与坐标原点重合, , ,当A点在反比例函数 的图象上移动时,B点坐标满足的函数解析式为 .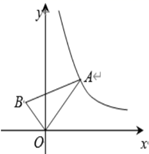 15. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .16. 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为米.
15. 若函数y=mx2+2x+1的图象与x轴只有一个公共点,则常数m的值是 .16. 某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为米.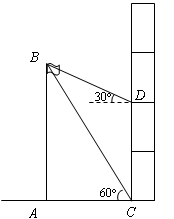 17. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .
17. 如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为 .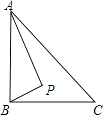 18. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)
18. 如图,已知直线 : ,过点 作x轴的垂线交直线 于点 ,在线段 右侧作等边三角形 ,过点 作x轴的垂线交x轴于 ,交直线L于点 ,在线段 右侧作等边三角形 ,按此作法继续下去则 的纵坐标为 . (n为正整数)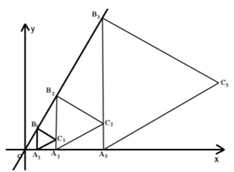
三、解答题
-
19.(1)、计算: ;(2)、先化简,再求代数式 的值,其中x是不等式组 的整数解.20. 为迎接2020年第35届全国青少年科技创新大赛,某学校举办了A:机器人;B:航模;C:科幻绘画;D:信息学;E:科技小制作等五项比赛活动(每人限报一项),将各项比赛的参加人数绘制成如图两幅不完整的统计图.
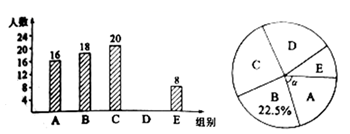
根据统计图中的信息解答下列问题:
(1)、本次参加比赛的学生人数是名;(2)、把条形统计图补充完整;(3)、求扇形统计图中表示机器人的扇形圆心角 的度数;(4)、在C组最优秀的3名同学(1名男生2名女生)和E组最优秀的3名同学(2名男生1名女生)中,各选1名同学参加上一级比赛,利用树状图或表格,求所选两名同学中恰好是1名男生1名女生的概率.21. 如图,直线 与双曲线 相交于 , 两点,与x轴交于点E,与y轴相交于点C.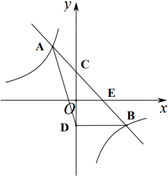 (1)、求m,n的值;(2)、若点D与点C关于x轴对称,求 的面积;22. 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
(1)、求m,n的值;(2)、若点D与点C关于x轴对称,求 的面积;22. 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆. (1)、试判断直线AB与⊙O的位置关系,并说明理由;(2)、若AC=8,tan∠DAC=
(1)、试判断直线AB与⊙O的位置关系,并说明理由;(2)、若AC=8,tan∠DAC=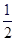 ,求⊙O的半径. 23. 为切实做好新冠疫情防控工作,我区某校准备在药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.24.
,求⊙O的半径. 23. 为切实做好新冠疫情防控工作,我区某校准备在药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.24.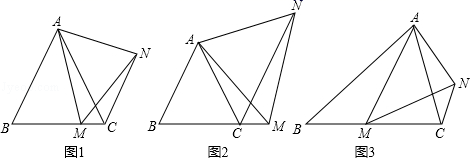 (1)、(提出问题)
(1)、(提出问题)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
(2)、(类比探究)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
(3)、(拓展延伸)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
25. 已知,经过点A(-4,4)的抛物线y=ax2+bx与x轴相交于点B(-3,0).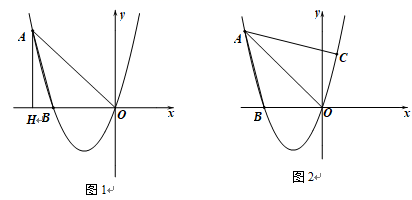 (1)、求抛物线的解析式;(2)、如图1,过点A作AH⊥x轴,垂足为H , 平行于y轴的直线交线段AO于点Q , 交抛物线于点P , 当四边形AHPQ为平行四边形时,求∠AOP的度数;(3)、如图2,试探究:在抛物线上是否存在点C , 使∠CAO=∠BAO?若存在,请求出直线AC解析式;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图1,过点A作AH⊥x轴,垂足为H , 平行于y轴的直线交线段AO于点Q , 交抛物线于点P , 当四边形AHPQ为平行四边形时,求∠AOP的度数;(3)、如图2,试探究:在抛物线上是否存在点C , 使∠CAO=∠BAO?若存在,请求出直线AC解析式;若不存在,请说明理由.