山东省滨州市阳信县2021年中考数学一模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、单选题
-
1. 计算|﹣1|﹣3,结果正确的是( )A、﹣4 B、﹣3 C、﹣2 D、﹣12. 下列运算正确的是( )A、 B、 C、 D、3. 据央视网消息,全国广大共产党员积极响应党中央号召,踊跃捐款,表达对新冠肺炎疫情防控工作的支持,据统计,截至2020年3月26日,全国已有7901万多名党员自愿捐款,共捐款82.6亿元,82.6亿用科学记数法可表示为( )A、 B、 C、 D、4. 函数 的自变量x的取值范围是( )A、 B、 且 C、 D、 且5. 某班级开展“好书伴成长”读书活动,统计了1至7月份该班同学每月阅读课外书的数量,绘制了折线统计图,下列说法正确的是( )
 A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多456. 如图1是用5个相同的正方体搭成的立体图形,若由图1变化至图2,则三视图中没有发生变化的是( )
A、每月阅读课外书本数的众数是45 B、每月阅读课外书本数的中位数是58 C、从2到6月份阅读课外书的本数逐月下降 D、从1到7月份每月阅读课外书本数的最大值比最小值多456. 如图1是用5个相同的正方体搭成的立体图形,若由图1变化至图2,则三视图中没有发生变化的是( )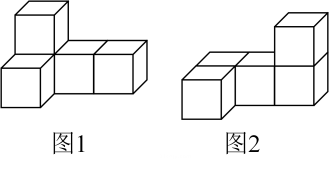 A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图7. 不等式组 的解集在数轴上表示正确的是( )A、
A、主视图 B、主视图和左视图 C、主视图和俯视图 D、左视图和俯视图7. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、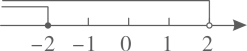 C、
C、 D、
D、 8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD为⊙O的弦,AB⊥CD于点E , 若CD=6 ,AE=9,则阴影部分的面积为( )
8. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、9. 如图,AB是⊙O的直径,CD为⊙O的弦,AB⊥CD于点E , 若CD=6 ,AE=9,则阴影部分的面积为( ) A、6π﹣ B、12π﹣9 C、3π﹣ D、910. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
A、6π﹣ B、12π﹣9 C、3π﹣ D、910. 如图, 中, ,点D在 上, .若 ,则 的长度为( )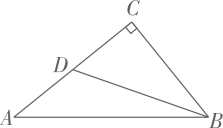 A、 B、 C、 D、411. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( )
A、 B、 C、 D、411. 如图1,点P从 的顶点A出发,沿 匀速运动到点C,图2是点P运动时线段 的长度y随时间x变化的关系图象,其中点Q为曲线部分的最低点,则 的边 的长度为( ) A、12 B、8 C、10 D、1312. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )
A、12 B、8 C、10 D、1312. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )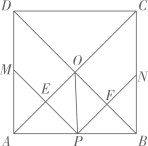 A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤
A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤二、填空题
-
13. 因式分解: .14. 如果关于x的一元二次方程kx2﹣3x+1=0有两个实数根,那么k的取值范围是 .15. 菱形的一条对角线长为8,其边长是方程x2﹣9x+20=0的一个根,则该菱形的面积为 .16. 将抛物线 向上平移3个单位长度后,经过点 ,则 的值是 .17. 在平面直角坐标系中,点A的坐标是 ,以原点O为位似中心,把线段OA放大为原来的2倍,点A的对应点为 .若点 恰在某一反比例函数图象上,则该反比例函数的解析式为 .18. 如图,将正方形网格放置在平面直角坐标系中,其中,每个小正方形的边长均为1,点A , B , C的坐标分别为 , , . 是 关于 轴的对称图形,将 绕点 逆时针旋转180°,点 的对应点为M , 则点M的坐标为 .
 19. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .
19. 如图,P为平行四边形 边 上一点, 分别为 上的点,且 的面积分别记为 .若 则 .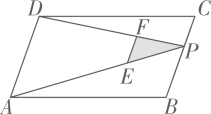 20. 已知k为正整数,无论k取何值,直线 与直线 都交于一个固定的点,这个点的坐标是;记直线 和 与x轴围成的三角形面积为 ,则 , 的值为 .
20. 已知k为正整数,无论k取何值,直线 与直线 都交于一个固定的点,这个点的坐标是;记直线 和 与x轴围成的三角形面积为 ,则 , 的值为 .三、解答题
-
21.(1)、计算:2﹣1+| ﹣3|+2 sin45°﹣(﹣2)2021•( )2021 .(2)、先化简,再求值:( )÷ ,其中a满足a2+2a﹣15=0.22. 东营市某中学对2020年4月份线上教学学生的作业情况进行了一次抽样调查,根据收集的数据绘制了下面不完整的统计图表.
作业情况
频数
频率
非常好
0.22
较好
68
一般
不好
40
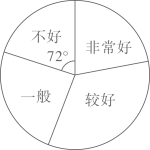
请根据图表中提供的信息,解答下列问题:
(1)、本次抽样共调查了多少名学生?(2)、将统计表中所缺的数据填在表中横线上;(3)、若该中学有1800名学生,估计该校学生作业情况“非常好”和“较好”的学生一共约多少名?(4)、某学习小组4名学生的作业本中,有2本“非常好”(记为 ), 本“较好”(记为 ),1本“一般”(记为C),这些作业本封面无姓名,而且形状、大小、颜色等外表特征完全相同,从中抽取一本,不放回, 从余下的3本中再抽取一本 ,请用“列表法”或“画树状图”的方法求出两次抽到的作业本都是“非常好”的概率.23. 为了测量一条两岸平行的河流宽度,三个数学研究小组设计了不同的方案,他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向.测量方案与数据如下表:课题
测量河流宽度
测量工具
测量角度的仪器,皮尺等
测量小组
第一小组
第二小组
第三小组
测量方案示意图
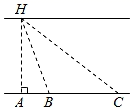
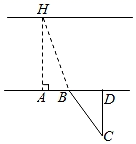
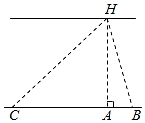
说明
点B,C在点A的正东方向
点B,D在点A的正东方向
点B在点A的正东方向,点C在点A的正西方向.
测量数据
BC=60m,
∠ABH=70°,
∠ACH=35°.
BD=20m,
∠ABH=70°,
∠BCD=35°.
BC=101m,
∠ABH=70°,
∠ACH=35°.
 (1)、哪个小组的数据无法计算出河宽?(2)、请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)24. 今年植树节期间,某景观园林公司购进一批成捆的A,B两种树苗,每捆 种树苗比每捆B种树苗多10棵,每捆A种树苗和每捆B种树苗的价格分别是630元和600元,而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.(1)、求这一批树苗平均每棵的价格是多少元?(2)、如果购进的这批树苗共5500棵,A种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进A种树苗和B种树苗各多少棵?并求出最低费用.25. 如图,在 中, , 平分 交 于点D,O为 上一点,经过点A、D的 分别交 、 于点E、F.
(1)、哪个小组的数据无法计算出河宽?(2)、请选择其中一个方案及其数据求出河宽(精确到0.1m).(参考数据:sin70°≈0.94,sin35°≈0.57,tan70°≈2.75,tan35°≈0.70)24. 今年植树节期间,某景观园林公司购进一批成捆的A,B两种树苗,每捆 种树苗比每捆B种树苗多10棵,每捆A种树苗和每捆B种树苗的价格分别是630元和600元,而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.(1)、求这一批树苗平均每棵的价格是多少元?(2)、如果购进的这批树苗共5500棵,A种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进A种树苗和B种树苗各多少棵?并求出最低费用.25. 如图,在 中, , 平分 交 于点D,O为 上一点,经过点A、D的 分别交 、 于点E、F. (1)、求证: 是 的切线;(2)、若 , ,求 的半径;(3)、求证: .26. 已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(-1,0),交y轴于点C.
(1)、求证: 是 的切线;(2)、若 , ,求 的半径;(3)、求证: .26. 已知抛物线y=ax2+bx+6(a≠0)交x轴于点A(6,0)和点B(-1,0),交y轴于点C. (1)、求抛物线的解析式和顶点坐标;(2)、如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴,y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;(3)、如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.
(1)、求抛物线的解析式和顶点坐标;(2)、如图(1),点P是抛物线上位于直线AC上方的动点,过点P分别作x轴,y轴的平行线,交直线AC于点D,E,当PD+PE取最大值时,求点P的坐标;(3)、如图(2),点M为抛物线对称轴l上一点,点N为抛物线上一点,当直线AC垂直平分△AMN的边MN时,求点N的坐标.