青海省海东市2021年中考数学一模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、填空题
-
1. 2021的倒数为; 的立方根为 .2. 分解因式: ;分式方程: 解为 .3. 去年“五一”假期,我市某主题公园共接待游客96800人次,将96800用科学记数法表示为 .4. 为创建“国家生态园林城市”,某小区在规划设计时,在小区中央设置一块面积为1200平方米的矩形绿地,并且长比宽多40米.设绿地宽为x米,根据题意,可列方程为 .
5. 已知一次函数 的图象与反比例函数 的图象交于点 ,若 =2,则反比例函数的表达式为 .6. 如图,菱形 的对角线 、 交于点O , 点E、F、G分别在 、 、 上,且四边形 为矩形.若 , ,则 的长为 .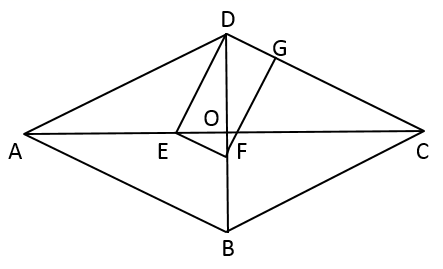 7. 如图,利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是 .
7. 如图,利用标杆 测量建筑物的高度,已知标杆 高 ,测得 , ,则建筑物 的高是 .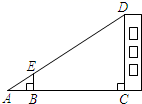 8. 某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 .
8. 某十字路口设有交通信号灯,东西向信号灯的开启规律如下:红灯开启30秒后关闭,紧接着黄灯开启3秒后关闭,再紧接着绿灯开启42秒,按此规律循环下去.如果不考虑其他因素,当一辆汽车沿东西方向随机地行驶到该路口时,遇到红灯的概率是 . 9. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .
9. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .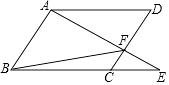 10. 如图是一个数值转换机示意图,当 , 时,输出的结果为 .
10. 如图是一个数值转换机示意图,当 , 时,输出的结果为 .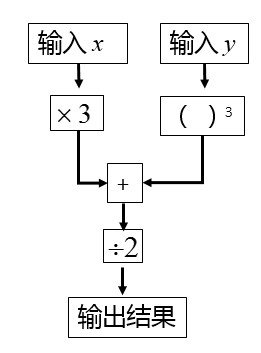 11. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道 尺(1尺=10寸),则该圆材的直径为寸.
11. 《九章算术》作为古代中国乃至东方的第一部自成体系的数学专著,与古希腊的《几何原本》并称现代数学的两大源泉.在《九章算术》中记载有一问题“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺,问径几何?”小辉同学根据原文题意,画出圆材截面图如图所示,已知:锯口深为1寸,锯道 尺(1尺=10寸),则该圆材的直径为寸.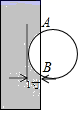 12. 观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第2021个图形中共有个○,第n个图形中共有个○.
12. 观察如图所示的一系列图形,它们是按一定规律排列的,依照此规律,第2021个图形中共有个○,第n个图形中共有个○.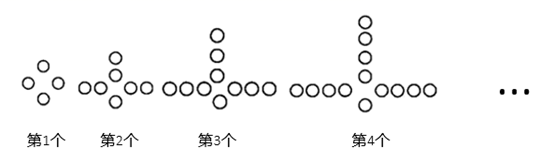
二、单选题
-
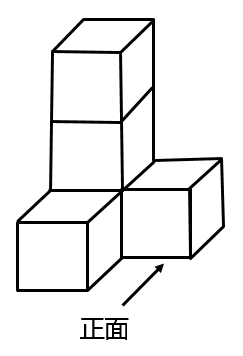
13. 如图所示的几何体由5个大小相同的小立方块组成,它的左视图为( )
 A、
A、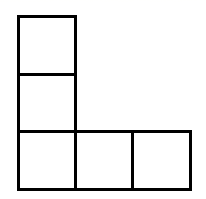 B、
B、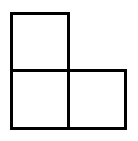 C、
C、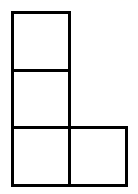 D、
D、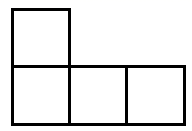 14. 如图, ,l3分别与 、 相交,点A为 上一点, 于点B , 若 ,则 的度数为( )
14. 如图, ,l3分别与 、 相交,点A为 上一点, 于点B , 若 ,则 的度数为( )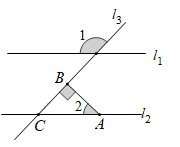 A、28° B、42° C、38° D、32°15. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、16. 为了解某校学生今年元宵节期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图.已知该校共有1000名学生据此估计,该校元宵节期间参加社团活动时间在8~10小时之间的学生人数大约是( )
A、28° B、42° C、38° D、32°15. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、16. 为了解某校学生今年元宵节期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘成如图所示的频数分布直方图.已知该校共有1000名学生据此估计,该校元宵节期间参加社团活动时间在8~10小时之间的学生人数大约是( )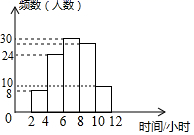 A、360名 B、320名 C、300名 D、280名17. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )
A、360名 B、320名 C、300名 D、280名17. 如图,在 中,将 沿AC折叠后,点D恰好落在DC的延长线上的点E处.若 , ,则 的周长为( )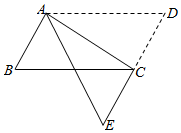 A、12 B、15 C、18 D、2118. 如图,在 中, , ,过点A作 的垂线交 于点D , 平分 交 于点E . 若 ,则 的长为( )
A、12 B、15 C、18 D、2118. 如图,在 中, , ,过点A作 的垂线交 于点D , 平分 交 于点E . 若 ,则 的长为( )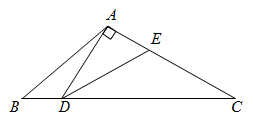 A、 B、 C、 D、319. 如图,将⊙O沿弦 折叠, 恰好经过圆心O , 若⊙O的半径为6,则 的长为( )
A、 B、 C、 D、319. 如图,将⊙O沿弦 折叠, 恰好经过圆心O , 若⊙O的半径为6,则 的长为( )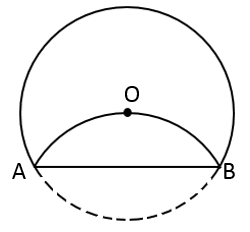 A、 B、π C、 D、20. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )
A、 B、π C、 D、20. 如图,平行四边形ABCD中,对角线AC、BD相交于点O,且AC=6,BD=8,P是对角线BD上任意一点,过点P作EF∥AC,与平行四边形的两条边分别交于点E、F.设BP=x,EF=y,则能大致表示y与x之间关系的图象为( )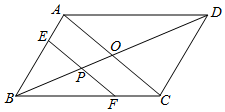 A、
A、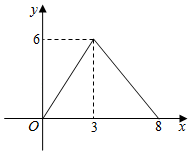 B、
B、 C、
C、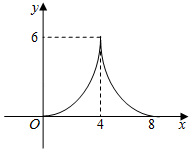 D、
D、
三、解答题
-
21. 计算:22. 计算 .23. 如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G .
 (1)、求证: BF=CF ;
(1)、求证: BF=CF ;
(2)、若 , ,求FG的长.24. 亚洲文明对话大会召开期间,大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场,若单独调配36座新能源客车若干辆,则有2人没有座位;若只调配22座新能源客车,则用车数量将增加4辆,并空出2个座位.(1)、计划调配36座新能源客车多少辆?该大学共有多少名志愿者?(2)、若同时调配36座和22座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?25. 如图,M,N是以AB为直径的⊙O上的点,且 = ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F. (1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.26. 在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).
(1)、求证:MF是⊙O的切线;(2)、若CN=3,BN=4,求CM的长.26. 在“优秀传统文化进校园”活动中,学校计划每周二下午第三节课时间开展此项活动,拟开展活动项目为:剪纸,武术,书法,器乐,要求七年级学生人人参加,并且每人只能参加其中一项活动.教务处在该校七年级学生中随机抽取了100名学生进行调查,并对此进行统计,绘制了如图所示的条形统计图和扇形统计图(均不完整).

请解答下列问题:
(1)、请补全条形统计图和扇形统计图;
(2)、在参加“剪纸”活动项目的学生中,男生所占的百分比是多少?(3)、若该校七年级学生共有500人,请估计其中参加“书法”项目活动的有多少人?
(4)、学校教务处要从这些被调查的女生中,随机抽取一人了解具体情况,那么正好抽到参加“器乐”活动项目的女生的概率是多少?27. 如图1,矩形ABCD中,点E为AB边上的动点(不与A,B重合),把 沿DE翻折,点A的对应点为 ,延长 交直线DC于点F,再把 折叠,使点B的对应点 落在EF上,折痕EH交直线BC于点H.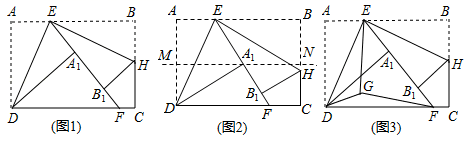 (1)、求证: ;(2)、如图2,直线MN是矩形ABCD的对称轴,若点 恰好落在直线MN上,试判断 的形状,并说明理由;(3)、如图3,在(2)的条件下,点G为 内一点,且 ,试探究DG,EG,FG的数量关系.28. 如图,在平面直角坐标系中,已知点B的坐标为 ,且 ,抛物线 图象经过 三点.
(1)、求证: ;(2)、如图2,直线MN是矩形ABCD的对称轴,若点 恰好落在直线MN上,试判断 的形状,并说明理由;(3)、如图3,在(2)的条件下,点G为 内一点,且 ,试探究DG,EG,FG的数量关系.28. 如图,在平面直角坐标系中,已知点B的坐标为 ,且 ,抛物线 图象经过 三点.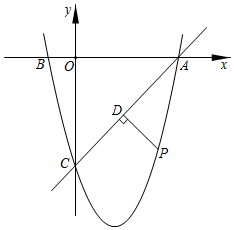 (1)、求 两点的坐标;(2)、求抛物线的解析式;(3)、若点 是直线 下方的抛物线上的一个动点,作 于点 ,当 的值最大时,求此时点 的坐标及 的最大值.
(1)、求 两点的坐标;(2)、求抛物线的解析式;(3)、若点 是直线 下方的抛物线上的一个动点,作 于点 ,当 的值最大时,求此时点 的坐标及 的最大值.