广东省江门市恩平市2021年中考数学模拟试卷

试卷更新日期：2021-06-16 类型：中考模拟

进入出卷网下载

一、单选题

1. -2021的倒数是（）

A、2021 B、 $\frac{1}{2021}$ C、 $- 2021$ D、 $- \frac{1}{2021}$

查看试题解析
2. 若有理数a ， b在数轴上的对应点的位置如图所示，则下列结论正确的是（）

A、 $b < 4$ B、 $- a > b$ C、 $| a | < | b |$ D、 $- a b < 0$

查看试题解析
3. 一个几何体的三视图如图所示，则该几何体为（）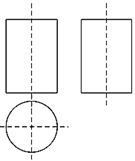

A、圆柱 B、圆锥 C、四棱柱 D、四棱锥

查看试题解析
4. 为了将“新冠”疫情对国民经济的影响降至最低，中国政府采取积极的财政税收政策，切实减轻企业负担，以促进我国进出口企业平稳发展，据国家统计局相关数据显示，2020年1月至5月，全国累计办理出口退税6324亿元，其中6324亿用科学记数法表示为（）

A、 $6.324 \times 10^{11}$ B、 $6.324 \times 10^{10}$ C、 $632 .4 \times 10^{9}$ D、 $0.6324 \times 10^{12}$

查看试题解析
5. 在平面直角坐标系中，已知点 $A (a, 2)$ ， $B (1, b)$ 关于原点对称，则 $a^{2} + b$ 的值为（）

A、-1 B、1 C、3 D、5

查看试题解析
6. 下列表述中，正确的是（）

A、“任意一个五边形的外角和是540°”是必然事件 B、抛掷一枚质地均匀的硬币100次，正面朝上的次数正好为50次 C、抛掷两枚质地均匀的银币，正好一枚正面朝上，一枚反面朝上的概率为 $\frac{1}{2}$ D、“367人中至少有两人的生日相同”是随机事件

查看试题解析
7. 已知 $\sqrt{a - 13} + \sqrt{13 - a} = b + 10$ ，则 $\sqrt{2 a - b}$ 的值为（）

A、6 B、 $\pm 6$ C、4 D、 $\pm 4$

查看试题解析
8. 若关于x的分式方程 $\frac{3 x}{x - 2}$ ＝ $\frac{m}{2 - x}$ +5的解为正数，则m的取值范围为（）

A、m＜﹣10 B、m≤﹣10 C、m≥﹣10且m≠﹣6 D、m＞﹣10且m≠﹣6

查看试题解析
9. 已知关于x的不等式组 ${\begin{array}{l} x - a > 0 \\ 5 - 2 x > 1 \end{array}$ 有三个整数解，则a的取值范围是（）

A、 $- 2 < a < - 1$ B、 $- 2 \leq a < - 1$ C、 $- 2 \leq a \leq - 1$ D、 $- 2 < a < 0$

查看试题解析
10. 如图，点A在双曲线 $y = - \frac{k}{x} (x < 0)$ 上，连接 $O A$ ，作 $O B ⊥ O A$ ，交双曲线 $y = \frac{8}{x} (x > 0)$ 于点B ，连接 $A B$ ．若 $\sin B = \frac{3}{5}$ ，则k的值为（）

A、1 B、2 C、 $\frac{9}{4}$ D、 $\frac{9}{2}$

查看试题解析

二、填空题

11. 分解因式： $4 x^{3} y^{2} - x^{3} =$ ．

查看试题解析
12. 若 $| a + 2 |$ +（b﹣3）²＝0，则a^b＝．

查看试题解析
13. 已知 $3 x^{2} + 2 x - 3$ 的值为6，则 $2 - x^{2} - \frac{2}{3} x$ 的值为．

查看试题解析
14. 如图， $A B$ ， $A C$ 是 $⊙ O$ 的切线，B ， C为切点， $B E$ 是 $⊙ O$ 的直径，延长 $B E$ 交 $A C$ 的延长线于点D，连接 $B C$ ．若 $∠ D B C = 25 °$ ，则 $∠ B D C$ 的度数为．

查看试题解析
15. 如图，在矩形 $A B C D$ 中，E是 $B C$ 的中点， $D F ⊥ A E$ ，垂足为F ．若 $A B = 6$ ， $B C = 4$ ，则 $D F$ 的长为．

查看试题解析
16. 观察下列式子： $1 \times 3 + 1 = 4 = 2^{2}$ ， $2 \times 4 + 1 = 9 = 3^{2}$ ， $3 \times 5 + 1 = 16 = 4^{2}$ ，…根据上述规律，写一个类似的式子：．

查看试题解析
17. 如图，四边形 $A B C D$ 是边长为a的正方形，点E是边 $B C$ 上一动点（不与点B ， C重合）， $∠ A E F = 90 °$ ，且EF交正方形外角的平分线 $C F$ 于点F ，交 $C D$ 于点G ，连接 $A F$ ．有下列结论：① $A E = E F$ ；② $C F = \sqrt{2} B E$ ；③ $∠ D A F = ∠ C F E$ ；④ $△ C E F$ 面积的最大值为 $\frac{1}{4} a^{2}$ ．其中正确的是．（把正确结论的序号都填上）

查看试题解析

三、解答题

18. 计算： $2 \sin 60 ° - {(- \frac{1}{3})}^{- 2} + {(π - 2021)}^{0}$ ．

查看试题解析
19. 先化简，再求值： $\frac{m + n}{m} \div (\frac{- m^{2} - n^{2}}{m} - 2 n)$ ，其中 $m + n = - 3$ ．

查看试题解析
20. 某校为了解九年级学生“一分钟跳绳”体育测试项目情况，随机抽取了九年级部分学生组成测试小组行调查测试，对这部分学生“一分钟跳绳”测试的成绩按A ， B ， C ， D四个等级进行了统计，并绘制了如图所示的不完整统计图．

(1)、本次抽样调查的样本容量为，并将条形统计图补充完整；

(2)、若该校九年级共有400名学生，根据以上样本估计全校九年级“一分钟跳绳”测试成绩为A等级的学生人数．

查看试题解析
21. 如图， $△ A B C$ 为等腰三角形， $A B = A C$ ．

(1)、尺规作图：作 $A B$ 的垂直平分线，交 $A C$ 于点D ，交 $A B$ 于点E（保留作图痕迹，不要求写作法）；

(2)、连接 $B D$ ，若 $B D = B C$ ，求 $∠ A$ 的度数．

查看试题解析
22. 某服装店自2018年以来，销售成衣数量在稳健地上涨，2018年全年售出10000件成衣，2020年全年售出14400件成衣．

(1)、求该服装店2018年到2020年成衣销售量的年平均增长率；

(2)、若服装店售出成衣数量还将保持相同的年平均增长率，请你预算2022年该服装店售出成衣将达到多少件?

查看试题解析
23. 如图，已知 $A B$ 是 $⊙ O$ 的直径，点E是 $⊙ O$ 上一点，F为 $\overset{⌢}{E B}$ 的中点，过点F作 $A E$ 的垂线，垂足为C ，交 $A B$ 的延长线于点D ，连接 $A F$ ．

(1)、求证：直线 $C D$ 是 $⊙ O$ 的切线；

(2)、若 $B D = 2$ ， $\sin D = \frac{2}{3}$ ，求 $C D$ 的长．

查看试题解析
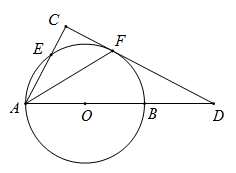24. 如图1，四边形 $A B C D$ 是矩形，点P是对角线 $A C$ 上的一个动点（不与点A ， C重合），过点P作 $P E ⊥ C D$ 于点E ，连接 $P B$ ，已知 $A D = 3$ ， $A B = 4$ ，设 $A P = m$ ．

(1)、当 $m = 1$ 时，求 $P E$ 的长；

(2)、当 $A P = P E$ 时，求m的值；

(3)、如图2，过点P作 $P F ⊥ P B$ 交 $C D$ 边于点F ，设 $C F = n$ ，试判断 $5 m + 4 n$ 的值是否发生变化，若不变，请求出它的值；若变化，请说明理由．

查看试题解析
25. 如图，已知抛物线 $y = x^{2} + b x + c$ 与x轴相交于 $A (- 1 ， 0)$ ， $B (m ， 0)$ 两点，与y轴相交于点 $C (0 ， - 3)$ ，抛物线的顶点为D ．

(1)、求抛物线的解析式；

(2)、若点E在x轴上，且 $∠ E C B = ∠ C B D$ ，求点E的坐标；

(3)、若P是直线 $B C$ 下方抛物线上任意一点，过点P作 $P H ⊥ x$ 轴于点H ，与 $B C$ 交于点M ．当线段 $P M$ 取到最大值时，若F为y轴上一动点，求 $P H + H F + \frac{\sqrt{2}}{2} C F$ 的最小值．

查看试题解析