广东省佛山市顺德区2021年中考数学二模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、单选题
-
1. ﹣2的绝对值是( )A、﹣2 B、1 C、2 D、2. 下列图形中,是轴对称图形但不是中心对称图形的是( )A、圆 B、等腰三角形 C、平行四边形 D、菱形3. 如图是一个可以自由转动的转盘.转动转盘,当指针停止转动时,指针落在红色区域的概率是( )
 A、1 B、 C、 D、4. 如图,△ ∽△ ,若 , , ,则 的长是( )
A、1 B、 C、 D、4. 如图,△ ∽△ ,若 , , ,则 的长是( ) A、2 B、3 C、4 D、55. 下列运算正确的是( )A、 B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、平行四边形的对角线互相平分 B、正方形的对角线相等且互相垂直平分 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形8. 如图,将直角三角板的直角顶点B放在 上,直角边 经过圆心O,则另一直角边 与 的位置关系为( )
A、2 B、3 C、4 D、55. 下列运算正确的是( )A、 B、 C、 D、6. 在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )A、 B、 C、 D、7. 下列命题是假命题的是( )A、平行四边形的对角线互相平分 B、正方形的对角线相等且互相垂直平分 C、对角线相等的平行四边形是矩形 D、对角线互相垂直的四边形是菱形8. 如图,将直角三角板的直角顶点B放在 上,直角边 经过圆心O,则另一直角边 与 的位置关系为( ) A、相交 B、相切 C、相离 D、无法确定9. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、10. 如图1,在四边形 中, ,直线 .当直线l沿射线 方向从点B开始向右平移时,直线l与四边形 的边分别相交于点E、F.设直线l向右平移的距离为x,线段 的长为y,且y与x的函数关系如图2所示.当 时, 的面积为( )
A、相交 B、相切 C、相离 D、无法确定9. 《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四足五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余 尺.将绳子对折再量长木,长木还剩余 尺,问木长多少尺,现设绳长 尺,木长 尺,则可列二元一次方程组为( )A、 B、 C、 D、10. 如图1,在四边形 中, ,直线 .当直线l沿射线 方向从点B开始向右平移时,直线l与四边形 的边分别相交于点E、F.设直线l向右平移的距离为x,线段 的长为y,且y与x的函数关系如图2所示.当 时, 的面积为( )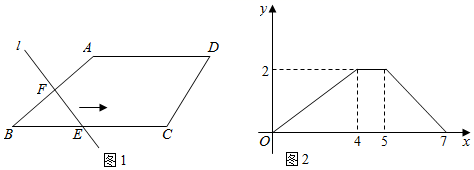 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 化简: = .12. 如果水位升高 时,水位变化记作 ,那么水位下降 时,水位变化记作m.13. 按照如图的操作步骤,若输入x的值为2,则输出的值是 . (用科学计算器计算或笔算)
 14. 已知 ,则 的余角大小是 .15. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .
14. 已知 ,则 的余角大小是 .15. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .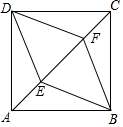 16. 定义新运算“ ”:对于任意实数 、 ,都有 ,例 .若 ,则x的值为 .17. 如图,在矩形 中,将 绕点D逆时针旋转 得到 ,使得B、F、E三点恰好在同一直线上, 与 相交于点G,连接 .以下结论正确的是 .
16. 定义新运算“ ”:对于任意实数 、 ,都有 ,例 .若 ,则x的值为 .17. 如图,在矩形 中,将 绕点D逆时针旋转 得到 ,使得B、F、E三点恰好在同一直线上, 与 相交于点G,连接 .以下结论正确的是 .
① ;
② ;
③点F是线段 的黄金分割点;
④ .
三、解答题
-
18. 解不等式组: .19. “直播+带货”是近年一种新兴的直播经济商业模式.为了解直播公益活动的情况,随机抽取甲、乙两个平台4月份其中6天的成交额如下:(单位:万元)
甲:7.6,8.6,9.0,9.4,9.7,9.7
乙:7.5,8.1,8.6,9.3,9.3,9.7
两组数据的平均数、中位数、众数如下表:
平台
平均数
中位数
众数
甲
a
b
9.7
乙
8.75
8.95
c
(1)、表格中 , ;(2)、请估算甲平台4月份的成交总额是多少?20. 如图 是一个锐角. (1)、用尺规作图法作出 的平分线 ;(2)、若点P是 上一点,过点P作 于点D, 于点E,求证: .21. 已知 .(1)、化简A;(2)、若A的值等于3,求x的值.22. 如图, 是半圆的直径,弦 ,过D点作圆O的切线 ,与 延长线相交于点E,连接 、 , .
(1)、用尺规作图法作出 的平分线 ;(2)、若点P是 上一点,过点P作 于点D, 于点E,求证: .21. 已知 .(1)、化简A;(2)、若A的值等于3,求x的值.22. 如图, 是半圆的直径,弦 ,过D点作圆O的切线 ,与 延长线相交于点E,连接 、 , .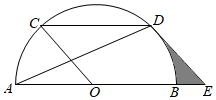 (1)、求证:四边形 是平行四边形;(2)、当 时,求围成阴影部分图形的周长.23. 如图,菱形 的顶点A、D的坐标分别是 、 ,顶点B在x轴上,反比例函数 的图象恰好经过点C.
(1)、求证:四边形 是平行四边形;(2)、当 时,求围成阴影部分图形的周长.23. 如图,菱形 的顶点A、D的坐标分别是 、 ,顶点B在x轴上,反比例函数 的图象恰好经过点C. (1)、求反比例函数的表达式;(2)、若点 、 、 都在反比例函数的图象上(其中 ),判断 与 的大小关系.24. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,每千克成本与销售月份之间的关系如图(2)所示(其中图(1)的图象是直线,图(2)的图象是抛物线).
(1)、求反比例函数的表达式;(2)、若点 、 、 都在反比例函数的图象上(其中 ),判断 与 的大小关系.24. 某地区在2020年开展脱贫攻坚的工作中大力种植有机蔬菜.某种蔬菜的销售单价与销售月份之间的关系如图(1)所示,每千克成本与销售月份之间的关系如图(2)所示(其中图(1)的图象是直线,图(2)的图象是抛物线). (1)、求每千克蔬菜销售单价y与销售月份x之间的关系式;(2)、判断哪个月份销售每千克蔬菜的收益最大?并求出最大收益;(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些?25. 已知抛物线 交x轴于点A、B,交y轴于点C,顶点为D,对称轴与x轴相交于点E.
(1)、求每千克蔬菜销售单价y与销售月份x之间的关系式;(2)、判断哪个月份销售每千克蔬菜的收益最大?并求出最大收益;(3)、求出一年中销售每千克蔬菜的收益大于1元的月份有哪些?25. 已知抛物线 交x轴于点A、B,交y轴于点C,顶点为D,对称轴与x轴相交于点E. (1)、直接写出 的值;(2)、点P在射线 上,以点P为圆心的圆经过A、B两点,且与直线 相切,求点P的坐标;(3)、点M在线段 下方的抛物线上,当 为锐角三角形时,求M点横坐标的取值范围.
(1)、直接写出 的值;(2)、点P在射线 上,以点P为圆心的圆经过A、B两点,且与直线 相切,求点P的坐标;(3)、点M在线段 下方的抛物线上,当 为锐角三角形时,求M点横坐标的取值范围.