吉林省长春市2021年中考数学二模试卷
试卷更新日期：2021-06-16 类型：中考模拟
一、选择题(本大题共8小题，每小题3分，共24分)
-
1. 人们通常把水结冰的温度记为0℃，而比水结冰的温度高3℃记为+3℃，那么比水结冰
的温度低5℃应记为（ ）
A、3℃ B、-3℃ C、5℃ D、-5℃2. 海关总署发布了2020年上半年中国外贸数据，整体表现好于预期．据统计，2020年上半年，我国货物贸易进口总值14 240 000 000 000元人民币，将14 240 000 000 000用科学记数法表示应为（ ）A、14.24×1012 B、1.424×1013 C、1.424×1014 D、14.24×10123. 由6个完全相同的小正方体搭成的几何体如图所示，它的俯视图是（ ）
A、
B、
C、
D、
4. 不等式x-1≥1的解集在数轴上表示为（ ）A、
B、
C、
D、
5. 如图，在地面上的点A处测得树顶B的仰角为α，AC=2，则树高BC为（ ）
A、2sinα B、2tanα C、2cosα D、6. 如图，四边形ABCD内接于⊙O，AB为直径，∠C=120°，若AD=2，则AB的长为（ ）
A、 B、2 C、2 D、47. 题目：已知∠AOB，求作射线OC，使OC平分∠AOB，如图，小刚按要求完成了作图，老师将他的作法打乱顺序叙述如下：①作射线OC，
②在射线OA和OB上分别截取OD，OE，使OD=OE
③分别以D，E为圆心，大于 DE的长为半径在∠AOB内作弧，两弧交于点C
那么作法的正确顺序是（ ）
A、①②③ B、②①③ C、②③① D、③①②8. 如图，在平面直角坐标系中，O为坐标原点，P是函数y= (x>0)图像上的一点，过点P作x轴的垂线交函数y=- (x>0)的图像于点A，过点A作y轴的垂线交PO的延长线于点B。若点P从左向右运动，则△ABP的面积（ ）
A、逐渐变大 B、逐渐变小 C、保持不变，且面积为9 D、保持不变，且面积为18二、填空题(本大题共6小题，每小题3分，共18分)
-
9. 计算(a2)3的结果是10. 某商场计划以每件75元的进价购进m件男士“T恤”衫．如果将这种男士“T恤”衫以每件100元售出，售完这批男士“T恤”衫获得的总利润是11. 一元二次方程x2-4x+1=0根的判别式的值为12. 如图，在正六边形ABCDEF的外侧作正方形ABGH，连结AC，AG，则∠CAG的大小为度
13. 如图，在△ABC中，AB=2，∠C=72°，以AB为直径的⊙O交边BC于点D，若D为边BC的中点，则 的长为(结果保留π)
14. 如图，在平面直角坐标系中，O为坐标原点，抛物线y=a(x-2)2+3(a<0)的顶点为A，与抛物线y=ax2+3交于x轴上方的点B，过点B作垂直于y轴的直线，分别交两条抛物线于C，D两点(C，D两点均不与点B重合)，连结AD，AC，CO，OD，则四边形ACOD的面积为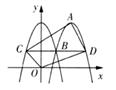
三、解答题(本大题共10小题，共78分)
-
15. 先化简，再求值：2(a2-3)-(a+2)(a-2)，其中a=16. 如图，三张不透明的卡片，正面图案分别是“人民英雄”国家荣誉称号获得者张伯礼、张定宇和陈薇的头像，依次记为A，B，C，卡片除正面图案不同外，其余均相同，将这三张卡片背面向上洗匀．小明从中随机抽取一张，记录图案后放回，重新洗匀后小华再从中随机抽取一张。请用画树状图(或列表)的方法，求小明和小华抽取的是同一位“人民英雄”的概率。
17. 随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4 200件，平均每人每周比原来多投递40件，若快递公司的快递员人数不变，求原来平均每人每周投递快件的件数。18. 图①、图②、图③均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，线段AB的端点在格点上，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，不要求写出画法，并保留作图痕迹，
(1)、在图①中以AB为边画一个面积为3的等腰三角形ABC；(2)、在图②中以AB为边画一个面积为3的钝角三角形ABD；(3)、在图③中以AB为边画一个面积为4的△ABE。19. 甲、乙、丙三个家电厂家在广告中都声称，他们的某种电子产品在正常情况下的使用寿命都是8年，经质量检测部门对这三家销售的产品的使用寿命进行跟踪调查，统计结果如下：(单位：年)甲厂：4，5，5，5，5，7，9，12，13，15
乙厂：6，6，8，8，8，9，10，12，14，15
丙厂：4，4，4，6，7，9，13，15，16，16
根据以上数据，绘制了下面不完整的表格：
平均数
众数
中位数
甲厂
8
5
6
乙厂
9.6
a
8.5
丙厂
9.4
4
b
根据以，上信息解答下列问题：
(1)、表格中a= ， b=(2)、这三个厂家的销售广告分别利用了哪一种表示集中趋势的特征数？(3)、如果这三个家电厂家的电子产品的售价相同，则顾客购买哪一家的电子产品更合适，并说明理由．20. 如图，在 ABCD中，E为边AB上一点，连结DE，将 ABCD沿DE翻折，使点A的对称点F落在边CD上，连结EF。
(1)、求证：四边形ADFE是菱形；(2)、若∠A=60°，AE=2BE=4，求四边形BCDE的周长。21. 某食品加工厂的甲、乙两个生产组领到了相同的加工任务，甲、乙两组以相同的工作效率同时开始工作，中途乙组因升级设备，停工了一段时间，乙组设备升级完毕后，提高了工作效率，在完成本组任务后，帮助甲组加工了60 kg食品，最后两组同时停工，完成了此次加工任务．两组各自加工的食品量y(kg)与甲组工作时间x(h)之间的函数图象如图所示。
(1)、甲组每小时加工食品kg，乙组升级设备后每小时加工食品kg；(2)、求乙组设备升级完毕后y与x之间的函数关系式；(3)、求m，n的值。22. [教材呈现]下图是华师版八年级下册数学教材第121页的部分内容。如图，在正方形ABCD中，CE⊥DF。
(1)、求证：CE=DF。
结合图①，写出证明过程。
(2)、[结论应用]如图②，设CE，DF相交于点G。若AB=3，图中阴影部分的面积和与正方形ABCD的面积之比为2：3，则△DCG的面积为 ， CG+DG的长为。
23. 如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD是斜边的中线，动点P从点A出发，以每秒5个单位长度的速度沿边AB向终点B运动，同时，动点Q从点A出发，沿折线AC-CB向终点B运动，在AC，CB上的速度分别为每秒8个单位长度和每秒6个单位长度．当点Q不与△ABC的顶点重合时，连结PQ，在直线AB上截取PN= PQ，使点C，N始终在PQ同侧，以PQ，PN为边作 PQMN。设点P的运动时间为t(s)。
(1)、求CD的长；(2)、当点M在中线CD上时，求t的值；(3)、当中线CD将 PQMN的面积两等分时，求BN的长；(4)、设O为中线CD的中点，作直线OQ。当直线OQ平分MN时，直接写出t的值。24. 在平面直角坐标系中，将函数y=-x2+mx +m+1(x≤m，m为常数)的图像记为G，点P的坐标为(m，- m2+m+ )。(1)、当点(0，3)在图像G上时，求m的值；(2)、当点P在图像G上时，求点P的坐标；(3)、当图像G的最高点的纵坐标与点P的纵坐标之差为1时，求m的值；(4)、将点P向左平移2个单位长度得到点Q，连结PQ，以PQ为边向上方作矩形PQMN，使PN=1。当图像G在矩形PQMN内的部分所对应的函数值y随x的增大而增大时，直接写出m的取值范围。