吉林省名校调研系列卷2021年中考数学三模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、选择题(每小题2分,共12分)
-
1. 下列各数中,最小的数是( )A、 B、 C、-2021 D、-12. 熔喷布,俗称口罩的“心脏”,是口罩中间的过滤层,能过滤细菌,阻止病菌传播,经测量,医用外科口罩的熔喷布厚度约为0.00156米,数据0.000156用科学记数法表示为( )A、0.156×10-3 B、1.56×10-3 C、15.6×10-4 D、1.56×10-43. 如图所示的几何体的左视图是( )
 A、
A、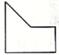 B、
B、 C、
C、 D、
D、 4. 不等式x+1<-1的解集在数轴上表示正确的是( )A、
4. 不等式x+1<-1的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、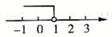 D、
D、 5. 如图,在△ABC中,AB=AC,在AB、AC上分别截取AP、AQ。使AP'=AQ。再分别以点P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D。若BC=6,则BD的长为( )
5. 如图,在△ABC中,AB=AC,在AB、AC上分别截取AP、AQ。使AP'=AQ。再分别以点P、Q为圆心,以大于 PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D。若BC=6,则BD的长为( )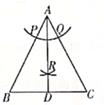 A、2 B、3 C、4 D、56. 中国美食讲究色香味美,优雅的摆盘造型:也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是一个摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C、D两点之间的距离为4cm,圆心角为60°,则图②的摆盘的面积是( )
A、2 B、3 C、4 D、56. 中国美食讲究色香味美,优雅的摆盘造型:也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是一个摆盘的几何示意图(阴影部分为摆盘),通过测量得到AC=BD=12cm,C、D两点之间的距离为4cm,圆心角为60°,则图②的摆盘的面积是( ) A、80πcm2 B、40πcm2 C、24πcm2 D、2πcm2
A、80πcm2 B、40πcm2 C、24πcm2 D、2πcm2二、填空题(每小题3分,共24 分)
-
7. 计算 ÷ 的结果是 .8. 分解因式:3x3-9x2=9. 若关于x的一元二次方程x2+k=0有实数根,则k的取值范围为10. 如图,直线PQ∥MN,将一个含有30°角的直角三角尺按如图所示的方式摆放。若∠CBA=43°,则∠PAC=度
 11. 如图,过正六边形ABCDEF的顶点B作一条射线,与其内角∠BAF的平分线相交于点P,且∠APB= 40°,则∠CBP=度
11. 如图,过正六边形ABCDEF的顶点B作一条射线,与其内角∠BAF的平分线相交于点P,且∠APB= 40°,则∠CBP=度 12. 如图,四边形ABCD内接于⊙O,连接BD,若 = ,∠BDC=50°,则∠ADC=度
12. 如图,四边形ABCD内接于⊙O,连接BD,若 = ,∠BDC=50°,则∠ADC=度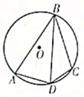 13. 如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,则此时小明离路灯杆AB的距离BD为m
13. 如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,则此时小明离路灯杆AB的距离BD为m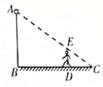 14. 如图,二次函数y= x2+4x+c的图象的顶点为A,与y轴的交点为B,BC∥x轴,交抛物线于点C,则△ABC的面积是
14. 如图,二次函数y= x2+4x+c的图象的顶点为A,与y轴的交点为B,BC∥x轴,交抛物线于点C,则△ABC的面积是
三、解答题(每小题5分,共20分)
-
15. 先化简,再求值:(x2y-2xy2-y)÷y-(x+y)(x-y)。其中x= ,y=116. 某社区有1名男管理员和3名女管理员,现要从中随机选取2名管理员参与“社区防控"宣讲活动。请用画树状图或列表的方法求恰好选到“1男1女”的概率。17. 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,O为对角线AC、BD的交点,且∠CAE=15°
 (1)、求证:△AOB是等边三角形;(2)、直接写出∠BOE的度数。18. 某公司要把240吨矿石运往A、B两地,现用大、小两种货车共20辆,怡好能一次性装完这批矿石(每辆货车均满载)。已知这两种货车的载重量分别为15吨/辆和10吨/辆。求这两种货车各用多少辆?
(1)、求证:△AOB是等边三角形;(2)、直接写出∠BOE的度数。18. 某公司要把240吨矿石运往A、B两地,现用大、小两种货车共20辆,怡好能一次性装完这批矿石(每辆货车均满载)。已知这两种货车的载重量分别为15吨/辆和10吨/辆。求这两种货车各用多少辆?四、解答题(每小题7分,共28分)
-
19. 如图,在6×6的正方形网格中。每个小正方形的边长均为1,点A、B均在小正方形的顶点上。
 (1)、在图①中画出 ABCD,点C、D均在小正方形的顶点上,且 ABCD的面积为16;(2)、在图②中画出以AB为底的等腰直角△ABE,点E在小正方形的顶点上;(3)、在图③中画出△ABF,使tan∠ABF= ,点F在小正方形的顶点上。20. 如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,在景区道路CD的C处测得栈道一端A位于北偏西42°方向,另一端B位于北偏东45°方向,又测得AC为100米,求木栈道AB的长度(结果保留整数。参考数据:sin42°≈ ,cos42°≈ ,tan42°≈ )。
(1)、在图①中画出 ABCD,点C、D均在小正方形的顶点上,且 ABCD的面积为16;(2)、在图②中画出以AB为底的等腰直角△ABE,点E在小正方形的顶点上;(3)、在图③中画出△ABF,使tan∠ABF= ,点F在小正方形的顶点上。20. 如图,某旅游景区为方便游客,修建了一条东西走向的木栈道AB,在景区道路CD的C处测得栈道一端A位于北偏西42°方向,另一端B位于北偏东45°方向,又测得AC为100米,求木栈道AB的长度(结果保留整数。参考数据:sin42°≈ ,cos42°≈ ,tan42°≈ )。 21. 如图,直线y= x与双曲线y= (k>0)交于A、B两点且点A的横坐标为4。
21. 如图,直线y= x与双曲线y= (k>0)交于A、B两点且点A的横坐标为4。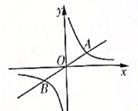 (1)、求k的值;(2)、若双曲线y= (k>0)上一点C的纵坐标为8,求△AOC的面积。22. 某学校八、九年级各有学生200人,为了提高学生的身体素质,学校开展了主题为“快乐运动、健康成长”的系列体育健身活动。为了了解学生的运动状况.从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成绩(百分制,且均为整数),并对数据(成绩)进行了整理、描述和分析。下面给出了部分信息(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)。
(1)、求k的值;(2)、若双曲线y= (k>0)上一点C的纵坐标为8,求△AOC的面积。22. 某学校八、九年级各有学生200人,为了提高学生的身体素质,学校开展了主题为“快乐运动、健康成长”的系列体育健身活动。为了了解学生的运动状况.从八、九年级各随机抽取40名学生进行了体能测试,获得了他们的成绩(百分制,且均为整数),并对数据(成绩)进行了整理、描述和分析。下面给出了部分信息(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)。a.八年级学生成绩的频数分布直方图如图(数据分为五组:50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100)

b.八年级学生成绩在70≤x<80这一组的数据如下:
70 71 73 73 73 74 76 77 78 79
c.九年级学生成绩的平均数、中位数、众数、优秀率如下:
平均数
中位数
众数
优秀率
79
76
84
40%
根据以上信息,回答下列问题.
(1)、在此次测试中,小腾的成绩是74分,在年级排名是第17名,由此可知他是年级的学生(填“八”或“九”);(2)、根据上述信息,推断年级学生运动状况更好,说明理由 (至少从两个不同的角度说明推断的合理性);(3)、假设八、九年级全体学生都参加了此次测试,估计九年级学生达到优秀的约有人五、解答题(每小题8分,共16分)
-
23. 小明和妈妈五一假期去看望外婆,返回时,他们先搭顺路车到A地。约定小明爸爸驾车到A地接他们回家,一家人恰好同时到达A地,休息半小时后,小明爸爸驾车返回家中。已知小明他们与外婆家的距离x(km)与小明从外婆家出发的时间t(h)之间的函数关系如图所示。
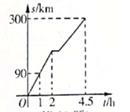 (1)、小明家与外婆家的距离是km;(2)、小明爸爸驾车返回时的平均速度是km/h;(3)、求他们从A地驾车返回家的过程中,s与t之间的函数关系式。24. AC是菱形ABCD的对角线,∠B=60°,AB=2,∠EAF=60°,将∠EAF绕顶点A旋转,∠EAF的两边分别与直线BC、CD交于点E、F,连接EF。
(1)、小明家与外婆家的距离是km;(2)、小明爸爸驾车返回时的平均速度是km/h;(3)、求他们从A地驾车返回家的过程中,s与t之间的函数关系式。24. AC是菱形ABCD的对角线,∠B=60°,AB=2,∠EAF=60°,将∠EAF绕顶点A旋转,∠EAF的两边分别与直线BC、CD交于点E、F,连接EF。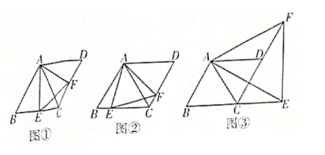 (1)、[感知]如图①,若E、F分别是边BC、CD的中点,则CE+CF =(2)、[探究]如图②,若E是线段BC上的任意一点,求CE+CF的长(3)、[应用]如图③,若E是线段BC的延长线上的一点,且EF⊥BC,则△AEF的周长为
(1)、[感知]如图①,若E、F分别是边BC、CD的中点,则CE+CF =(2)、[探究]如图②,若E是线段BC上的任意一点,求CE+CF的长(3)、[应用]如图③,若E是线段BC的延长线上的一点,且EF⊥BC,则△AEF的周长为六、解答题(每小题10分,共20分)
-
25. 如图,在平面直角坐标系中,抛物线y=- x2+bx的顶点为A,与x轴交于O、B两点,且点B的横坐标为4,连接OA、AB,直线y= x交AB;于点C、P为线段OC上一个动点,过点P作x轴的垂线交抛物线于点Q,以PQ为边向其右侧作矩形PQDE,且QD=1,设点p的横坐标为m。
 (1)、求抛物线的解析式;(2)、分别求点A、C的坐标;(3)、设矩形PQDE的周长为L,求L与m之间的函数关系式;(4)、当矩形PQDE与△OAB重叠部分图形为轴对称图形时,直接写出m的取值范围。26. 如图①,在△ABC中,∠ACB=90°,AC=8,BC=6,动点P从点A出发,以每秒1个单位长度的速度沿AC向终点C运动,动点Q从点C出发,以每秒2个单位长度的速段沿拆线CB-BA向终点A运动,连接PQ,以AP、PQ为邻边作平行四边形APQD。点P、Q同时出发,当有一个点到达终点时,另一个点也停止运动,设点p运动的时间为1(秒),平行四边形APQD与△ABC重叠部分的面积为S(平方单位)。
(1)、求抛物线的解析式;(2)、分别求点A、C的坐标;(3)、设矩形PQDE的周长为L,求L与m之间的函数关系式;(4)、当矩形PQDE与△OAB重叠部分图形为轴对称图形时,直接写出m的取值范围。26. 如图①,在△ABC中,∠ACB=90°,AC=8,BC=6,动点P从点A出发,以每秒1个单位长度的速度沿AC向终点C运动,动点Q从点C出发,以每秒2个单位长度的速段沿拆线CB-BA向终点A运动,连接PQ,以AP、PQ为邻边作平行四边形APQD。点P、Q同时出发,当有一个点到达终点时,另一个点也停止运动,设点p运动的时间为1(秒),平行四边形APQD与△ABC重叠部分的面积为S(平方单位)。 (1)、求点Q到边AC的距离(用含t的代数式表示);(2)、当点D落在边AB上时,求t的值;(3)、在点P运动的过程中,求S与t之间的函数关系式(S>0);(4)、如图②,动点P、Q出发的同时动点E从点C出发,以每秒3个单位长度的连度沿CA向终点A运动,当点E停止时,点P、Q也停止运动,连接DE,当DE所在的直线将平行四边形APQD的面积分成1:3两部分时,直接写出t的值。
(1)、求点Q到边AC的距离(用含t的代数式表示);(2)、当点D落在边AB上时,求t的值;(3)、在点P运动的过程中,求S与t之间的函数关系式(S>0);(4)、如图②,动点P、Q出发的同时动点E从点C出发,以每秒3个单位长度的连度沿CA向终点A运动,当点E停止时,点P、Q也停止运动,连接DE,当DE所在的直线将平行四边形APQD的面积分成1:3两部分时,直接写出t的值。