吉林省吉林市2021年中考数学二模试卷
试卷更新日期：2021-06-16 类型：中考模拟
一、单项选择题(每小题2分，共12分)
-
1. 如图，给出了吉林市2021年4月13日的最高气温和最低气温，则这天的温差是（ ）
A、-4℃ B、4℃ C、8℃ D、12℃2. 《中国5G经济报告2020》预计到2025年，中国5G用户将达到816 000 000，数据816 000 000用科学记数法表示为（ ）A、8.16×107 B、8.16×108 C、8.16×109 D、8.16×1093. 三星堆考古成果是中华文明多元- ．体发展模式的重要实物例证．下列出土文物从图案看不是轴对称图形的是（ ）A、
B、
C、
D、
4. 如图，一个倾斜的天平两边分别放有小立方体和砝码，每个砝码的质量都是5g，每个小立方体的质量都是m(g)，则m的取值范围为（ ）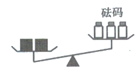
A、m>15 B、m<15 C、m> D、m<5. 如图，建筑工人砌墙时，经常在两个墙角的位置分别插一根木桩，然后拉一条直的参照线，其数学道理是（ ）
A、两点确定一条直线 B、两点之间，线段最短 C、垂线段最短 D、平行于同一条直线的两条直线平行6. 如图，直线a∥b，点A在直线b上，以点A为圆心，2cm长度为半径画弧，分别交直线a，b于C，B两点，连接AC，BC。若∠1=60°，则△ABC的周长为（ ）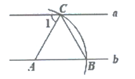
A、 cm B、2cm C、2 cm D、6cm二、填空题(每小题3分，共24分)
-
7. 计算： -2=8. 一本笔记本的原价是1n元，现在按8折出售，购买5本笔记本需要付费元9. 若分式 的值等于-3，则x=10. 若关于x的一元二次方程x2=c-1有实数根，则c的值可以为(写出一个即可)11. 如图，在Rt△ABC中，∠C=90°，∠BAC=40°，将Rt△ABC绕点A旋转得到Rt△AB'C'，且点C'落在AB上，则∠B'BC的度数为
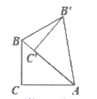12. 如图，在 ABCD中，BC=13，过点A作AE⊥DC于点E，AE=12，EC=10，则AB=
13. 大约在两千四五百年前，如图(1) 墨子和他的学生做了世界上第1个小孔成倒像的实验，并在《墨经》中有这样的精彩记录：“景到， 在午有端，与景长，说在端”。如图(2)所示的小孔成像实验中，若物距为10cm，像距为15cm，蜡烛火焰倒立的像的高度是6cm，则蜡烛火焰的高度是cm
14. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120°，扇面BD的长为20cm，扇面(阴影部分)的面积为 cm2 ， 则竹条AB的长为cm。
三、解答题(每小题5分，共20分)
-
15. 先化简，再求值：(a-2)2+4(a+1)，其中a=16. 如图，某飞镖游戏，A区为小圆内部，B区为大圆内小圆外部，掷到A区和B区的得分不同，每次掷中的位置用一个“X”标注。已知小红、小华有效成绩均为6次，结果小红得了54分，小华得了52分。求掷中A区，B区一次各得多少分？
17. 在全国政协2021新年茶话会上，习近平总书记强调要发扬“三牛”精神．如图，现有三张正面印有“三牛”图案的不透明卡片A，B，C，卡片除正面图案不同外，其余均相同。将三张卡片正面向下洗匀，小吉同学从中随机抽取两张卡片，请用画树状图或列表法求小吉同学抽出的两张卡片是A和B的概率。
18. 如图，AB是⊙O的直径，PB是⊙O的切线，连接AP交⊙O于点C。点D在⊙O上，∠CDB=45°，求证：AB=BP。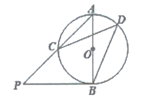
四、解答题(每小题7分，共28分)
-
19. 如图，4×4正方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A，B都在格点上，按下列要求作图，使得所画图形的顶点均在格点上。
(1)、在图①中画一个以线段AB为边的△ABC，使其面积为3 ；(2)、在图②中画一个以线段AB为边的轴对称四边形ABDE，使其面积为6；(3)、在图③中画一个以线段AB为边的中心对称四边形ABFG，使其面积为6。20. 2021年3月29日是我国第26个“全国中小学生安全教育日”。某校随机抽取了八年级学生的10%进行了一次安全知识测试，将这些学生的测试成绩(x)分为四个等级：优秀85≤x≤100；良好755x<85；及格60Sx<75；不及格0≤x<60。并绘制成如图两幅统计图。
根据以上信息，解答下列问题：
(1)、在抽取的学生中不及格人数所占的百分比是；(2)、若抽取的学生中不及格人数为2人，估算该校八年级学生的人数约为人，该校八年级学生中优秀等级的人数约为人；(3)、估算该校八年级学生此次测试成绩的平均分。21. 某人乘车从A地去B地．如图所示，B地在A地的正北方向，且距离A地9km，但A，B两地之间道路维修无法通过．按导航指示，车辆沿正西方向行驶至C地，再沿北偏东26°方向行驶到达B地，求车辆共行驶了多少千米(结果精确到0.1km)。(参考数据：sin26°=0.44，cos26°=0.90，tan26°=0.49)
22. “黄金1号”玉米种子的价格为5元/kg。如果一次购买2kg以上的种子，超过2kg部分的种子价格打8折。(1)、填表：购买量/kg
1
2
3
……
付款金额/元
……
(2)、直接写出付款金额关于购买量的函数解析式，并在给出的平面直角坐标系中画出函数图象。
五、解答题(每小题8分，共16分)
-
23. 如图，点P(3，2)在反比例函数y= (x>0)的图象上，过点P作PM∥x轴交反比例函数y= 的图象于点M，作PNIIy轴交反比例函数y= 的图象于点N，连接MN。
(1)、求k的值；(2)、求△PMN的面积；(3)、连接OM，ON，直接写出△MON的面积．24. 在四边形ABCD中，AB=AD=1，∠B=∠D=90°，点E为BC上一点(不与点B，点C重合)，连接AE，将△ABE沿AE翻折得到△AB'E，延长EB'交CD于点F。(1)、如图①，当∠C=90°时，四边形ABCD的形状为；
(2)、在(1)的条件下，随着点E位置的变化，△CEF的周长是否发生变化？若变化，请说明理由；若不变化，请求出它的值；(3)、如图②，当∠C=60°时，请直接写出△CEF的周长。
六、解答题(每小题10分，共20分)
-
25. 如图，在正方形ABCD中，AB=2，连接AC。P，Q两点分别从A，D同时出发，点P以每秒1个单位长度的速度沿线段AB向终点B运动；点Q沿折线D→A→C向终点C运动，在DA上的速度为每秒2个单位长度，在AC上的速度为每秒2 个单位长度。在运动过程中，以AP，AQ为邻边作平行四边形APMQ。设运动时间为x秒，平行四边形APMQ和正方形ABCD重叠部分的图形面积为y。
(1)、当点M在BC上时，x=(2)、求y关于x的函数解析式，并写出x的取值范围；(3)、连接MB，当0°<∠MBP<90°时，直接写出tan∠MBP= 时x的值。26. 如图，抛物线y=a(x+2)2-9a(a>0)与x轴相交于A，B两点(点A在点B的左侧)，顶点为C，连接BC。
(1)、直接写出点C的坐标(用含a的式子表示)；(2)、求点B的坐标：(3)、以BC为边，在BC边的右下方作正方形BCDE，设点D的坐标为(m，n)。①当∠ABC=30°时，求点D的坐标；
②当∠ABC=45°时，直接写出点D的坐标；
③直接写出n关于m的函数解析式及自变量m的取值范围。