山东省烟台招远市(五四制)2021年中考数学一模试卷
试卷更新日期:2021-06-17 类型:中考模拟
一、单选题
-
1. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 数学老师为了判断小颖的数学成绩是否稳定,对小颖在中考前的6次模拟考试中的成绩进行了统计,老师应最关注小颖这6次数学成绩的( )A、方差 B、中位数 C、平均数 D、众数4. 如图,已知 是平角, 平分 ,在平面上画射线 ,使 和 互余,若 ,则 的度数为( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 数学老师为了判断小颖的数学成绩是否稳定,对小颖在中考前的6次模拟考试中的成绩进行了统计,老师应最关注小颖这6次数学成绩的( )A、方差 B、中位数 C、平均数 D、众数4. 如图,已知 是平角, 平分 ,在平面上画射线 ,使 和 互余,若 ,则 的度数为( )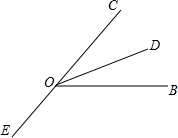 A、 B、 C、 或 D、 或5. 2020年的政府工作报告中,在回顾2019年的工作时提到:农村贫困人口减少1109万,贫困发生率降至 ,脱贫攻坚取得决定性成就.将数据1109万用科学记数法表示为( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、
A、 B、 C、 或 D、 或5. 2020年的政府工作报告中,在回顾2019年的工作时提到:农村贫困人口减少1109万,贫困发生率降至 ,脱贫攻坚取得决定性成就.将数据1109万用科学记数法表示为( )A、 B、 C、 D、6. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、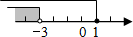 D、
D、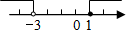 7. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是( )
7. 如图,已知 是 的直径, 是 的切线,连接 交 于点D,连接 .若 ,则 的度数是( )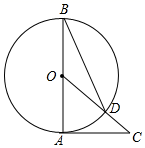 A、 B、 C、 D、8. 利用计算器求值时,小明将按键顺序为
A、 B、 C、 D、8. 利用计算器求值时,小明将按键顺序为 显示结果记为a,
显示结果记为a, 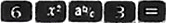 的显示结果记为b.则a,b的大小关系为( ) A、a<b B、a>b C、a=b D、不能比较9. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、10. 有下列四个函数:① ② ③ ④ ,其中图像经过如图所示的阴影部分(包括边界)的函数有( )
的显示结果记为b.则a,b的大小关系为( ) A、a<b B、a>b C、a=b D、不能比较9. 小刚身高 ,测得他站立在阳光下的影子长为 ,紧接着他把手臂竖直举起,测得影子长为 ,那么小刚举起的手臂超出头顶( )A、 B、 C、 D、10. 有下列四个函数:① ② ③ ④ ,其中图像经过如图所示的阴影部分(包括边界)的函数有( ) A、1 个 B、2个 C、3 个 D、4个11. 如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 , 与 轴分别交于 , 两点,若点 ,点 关于原点 对称,则 的最小值为( )
A、1 个 B、2个 C、3 个 D、4个11. 如图, 的半径为2,圆心 的坐标为 ,点 是 上的任意一点, ,且 , 与 轴分别交于 , 两点,若点 ,点 关于原点 对称,则 的最小值为( )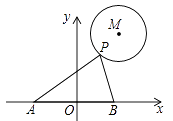
A、3 B、4 C、6 D、812. 已知二次函数 的图象如图所示,有以下结论:① ;② ;③ ;④ ;⑤ .其中所有正确结论的序号是( )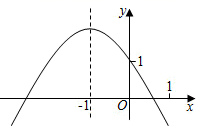 A、①② B、①③④ C、①②③④ D、①②③④⑤
A、①② B、①③④ C、①②③④ D、①②③④⑤二、填空题
-
13. -64的立方根是 。14. 已知 , 是一元二次方程 的两个实数根,则 的值是 .15. 如图,“赵爽弦图”是吴国的赵爽创制的.以直角三角形的斜边为边长得到一个正方形,该正方形由4个全等的直角三角形再加上中间的小正方形组成,在一次游园活动中,数学小组制作了一面“赵爽弦图锣”,其中 , , ,小明蒙上眼睛用棍子击中了锣面,他击中阴影部分的概率是 .
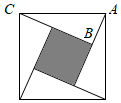 16. 如图,在矩形 中, , ,将矩形 绕点A逆时针旋转得到矩形 , 交 于点E,且 ,则 的长为 .
16. 如图,在矩形 中, , ,将矩形 绕点A逆时针旋转得到矩形 , 交 于点E,且 ,则 的长为 .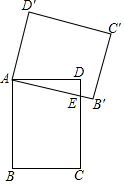 17. 如图,在扇形 中, ,点C为 的中点, 交 于点E,以点O为圆心, 的长为半径作 交 于点D.若 ,则图中阴影部分的面积为 .
17. 如图,在扇形 中, ,点C为 的中点, 交 于点E,以点O为圆心, 的长为半径作 交 于点D.若 ,则图中阴影部分的面积为 . 18. 如图, 为⊙O的直径, 是⊙O上的两点,过A作 于点C,过B作 于点D,P为 上的任意一点,若 , , ,则 的最小值是 .
18. 如图, 为⊙O的直径, 是⊙O上的两点,过A作 于点C,过B作 于点D,P为 上的任意一点,若 , , ,则 的最小值是 .
三、解答题
-
19. 先化简,再求值: ,其中x满足x2﹣4x+3=0.20. “金山银山,不如绿水青山”.各市区不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为 ,根据图表中的信息解答下列问题:
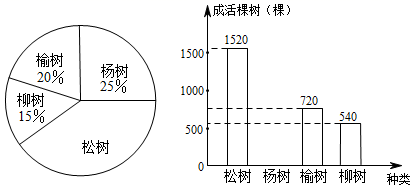 (1)、扇形统计图中松树所对的圆心角为度,并补全条形统计图 .(2)、该旗区今年共种树34万棵,成活了约多少棵?(3)、园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)21. 烟台苹果享誉全国.某水果超市计划从烟台购进“红富士”与“新红星”两种品种的苹果.已知3箱红富士苹果的进价与4箱新红星苹果的进价的和为396元,且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元(1)、求每箱“红富士”苹果的进价与每箱新红星苹果的进价分别是多少元?(2)、该水果超市计划再次购进100箱苹果,已知:“红富士”苹果的售价每箱65元,“新红星”苹果的售价每箱60元,根据市场的实际需求,“红富士”苹果的数量不低于“新红星”苹果数量的4倍.为使该水果超市售完这100箱苹果的总利润最大,该超市应如何进货?并求出最大利润.22. 如图, 内接于 , 为 的直径, 的延长线与过点A的直线相交于点E,且 .
(1)、扇形统计图中松树所对的圆心角为度,并补全条形统计图 .(2)、该旗区今年共种树34万棵,成活了约多少棵?(3)、园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)21. 烟台苹果享誉全国.某水果超市计划从烟台购进“红富士”与“新红星”两种品种的苹果.已知3箱红富士苹果的进价与4箱新红星苹果的进价的和为396元,且每箱红富士苹果的进价比每箱新红星苹果的进价贵6元(1)、求每箱“红富士”苹果的进价与每箱新红星苹果的进价分别是多少元?(2)、该水果超市计划再次购进100箱苹果,已知:“红富士”苹果的售价每箱65元,“新红星”苹果的售价每箱60元,根据市场的实际需求,“红富士”苹果的数量不低于“新红星”苹果数量的4倍.为使该水果超市售完这100箱苹果的总利润最大,该超市应如何进货?并求出最大利润.22. 如图, 内接于 , 为 的直径, 的延长线与过点A的直线相交于点E,且 .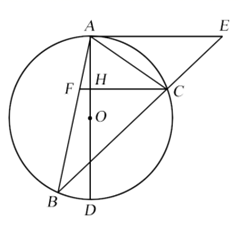 (1)、求证: 是 的切线;(2)、已知 , 与 , 分别相交于点F,H.若 , ,求 的值.23. 如图是小强洗漱时的侧面示意图,洗漱台(矩形 )靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ( ),身体前倾成 ( ),脚与洗漱台距离 (点D,C,G,E在同一直线上).
(1)、求证: 是 的切线;(2)、已知 , 与 , 分别相交于点F,H.若 , ,求 的值.23. 如图是小强洗漱时的侧面示意图,洗漱台(矩形 )靠墙摆放,高 ,宽 ,小强身高 ,下半身 ,洗漱时下半身与地面成 ( ),身体前倾成 ( ),脚与洗漱台距离 (点D,C,G,E在同一直线上).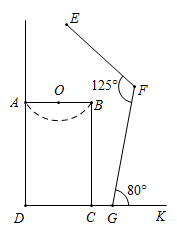 (1)、此时小强头部E点与地面 相距多少?(2)、小强希望他的头部E恰好在洗漱盆 的中点O的正上方,他应向前或后退多少?( , , ,计算结果精确到 )24.(1)、探究发现:
(1)、此时小强头部E点与地面 相距多少?(2)、小强希望他的头部E恰好在洗漱盆 的中点O的正上方,他应向前或后退多少?( , , ,计算结果精确到 )24.(1)、探究发现:如图1,将两块完全相同的含 的直角三角板斜边重合,拼成四边形 .P是对角线 上一动点, ,且点E在 延长线上, 交 于点F,连接 .通过探究可以求出: 的度数 .
(2)、拓展延伸: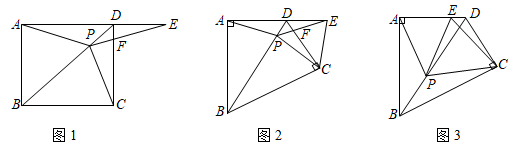
若将“含 的直角三角板”换成“含 ( )的直角三角板”,其他条件不变,如图2,直接写出 的度数 ;
(3)、若将“含 的直角三角形板”换成“含 ( )的直角三角板”,将“且点E在 延长线上”换成“且点E在线段 上(不与点A,D重合)”,其他条件不变,如图3,求 的度数(请说明理由);25. 如图,已知抛物线 与一直线相交于 , 两点,与y轴交于点N.其顶点为D. (1)、抛物线及直线 的函数关系式;(2)、若抛物线的对称轴与直线 相交于点B,E为直线 上的任意一点,过点E作 交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线 上方的一个动点,求 的面积的最大值.(4)、设点M的坐标为 ,直接写出使 的和最小时m的值.
(1)、抛物线及直线 的函数关系式;(2)、若抛物线的对称轴与直线 相交于点B,E为直线 上的任意一点,过点E作 交抛物线于点F,以B,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由;(3)、若P是抛物线上位于直线 上方的一个动点,求 的面积的最大值.(4)、设点M的坐标为 ,直接写出使 的和最小时m的值.