山东省聊城市茌平区、临清市2021年中考数学二模试卷

试卷更新日期：2021-06-16 类型：中考模拟

进入出卷网下载

一、单选题

1. -2的倒数是（）

A、-2 B、 $- \frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 把如图所示的纸片沿着虚线折叠，可以得到的几何体是（）

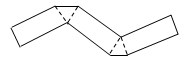A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥

查看试题解析
3. 下列运算正确的是（　　）

A、(ab)²＝ab² B、a²·a³= a⁶ C、(－ $\sqrt{2}$ )²＝4 D、m⁵÷m³＝m²

查看试题解析
4. 科学家在海底发现了世界上最小的生物，它们的最小身长只有 $0.000000019 m$ ．将 $0.000000019$ 这个数用科学记数法表示为（）

A、 $0.19 \times 10^{- 7}$ B、 $1.9 \times 10^{- 8}$ C、 $1.9 \times 10^{- 9}$ D、 $19 \times 10^{- 10}$

查看试题解析
5. 如图，实数a ， b在数轴上的对应点的位置如图所示，则正确的结论是（）

A、 $| a | > 3$ B、 $- 1 < - b < 0$ C、 $a < - b$ D、 $a + b > 0$

查看试题解析
6. 如图，△ABC内接于⊙O ，若∠A＝45°，OC＝2，则BC的长为（）

A、 $\sqrt{2}$ B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
7. 某中学为了解学生参加“青年大学习”网上班课的情况，对九年级 $6$ 个班的学习人数进行了统计，得到各班参加班课的人数数据为 $5, 10, 10, 12, 14, 9$ ．对于这组数据，下列说法错误的是（）

A、平均数是 $10$ B、众数是 $10$ C、中位数是 $11$ D、方差是 $\frac{23}{3}$

查看试题解析
8. 如图，菱形ABCD中，对角线AC ， BD相交于点O ， E为AB的中点．若菱形ABCD的周长为32，则OE的长为（）

A、3 B、4 C、5 D、6

查看试题解析
9. 如图，点A，B，C在正方形网格的格点上，则sin∠BAC=（）

A、 $\frac{\sqrt{2}}{6}$ B、 $\frac{\sqrt{26}}{26}$ C、 $\frac{\sqrt{26}}{13}$ D、 $\frac{\sqrt{13}}{13}$

查看试题解析
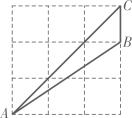10. 已知点（﹣2，a），（2，b），（3，c）在函数y＝ $\frac{k}{x}$ （k＞0）的图象上，则下列判断正确的是（　　）

A、a＜b＜c B、b＜a＜c C、a＜c＜b D、c＜b＜a

查看试题解析
11. 如图，点A ， B的坐标分别为 $A (2 ， 0) ， B (0 ， 2)$ ，点C为坐标平面内一点， $B C = 1$ ，点M为线段 $A C$ 的中点，连接 $O M$ ，则 $O M$ 的最大值为（）

A、 $\sqrt{2} + 1$ B、 $\sqrt{2} + \frac{1}{2}$ C、 $2 \sqrt{2} + 1$ D、 $2 \sqrt{2} - \frac{1}{2}$

查看试题解析
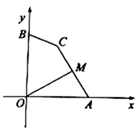12. 一组正方形按如图所示的方式放置，其中顶点B₁在y轴上，顶点C₁、E₁、E₂、C₂、E₃、E₄、C₃…在x轴上，已知正方形A₁B₁C₁D₁的边长为1，∠B₁C₁O＝60°，B₁C₁∥B₂C₂∥B₃C₃…则正方形A₂₀₁₇B₂₀₁₇C₂₀₁₇D₂₀₁₇的边长是（　　）

A、（ $\frac{1}{2}$ ）²⁰¹⁶ B、（ $\frac{1}{2}$ ）²⁰¹⁷ C、（ $\frac{\sqrt{3}}{3}$ ）²⁰¹⁶ D、（ $\frac{\sqrt{3}}{3}$ ）²⁰¹⁷

查看试题解析

二、填空题

13. 函数y= $\frac{1}{x + 3}$ 中，自变量x的取值范围是．

查看试题解析
14. 如图，若在象棋棋盘上建立直角坐标系，使“帥”位于点 $(- 3 ， - 2)$ ，“炮”位于点 $(- 2 ， 0)$ ，则“兵”位于的点的坐标为．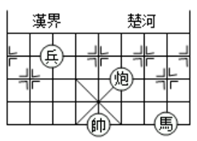

查看试题解析
15. 如图，从一块半径为 $1m$ 的圆形铁皮上剪出一个圆周角为120°的扇形 $A B C$ ，如果将剪下来的扇形围成一个圆锥，则该圆锥的底面圆的半径为 $m$ ．

查看试题解析
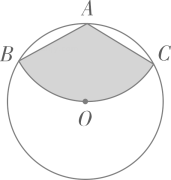16. 从满足不等式组 ${\begin{array}{l} 2 x + 1 \leq 7 \\ 3 x - 2 > - 11 \end{array}$ 的所有整数解中任意取一个数记作a ，则关于 $y$ 的一元二次方程 $a y^{2} - y - \frac{3}{4} = 0$ 有实数根的概率是．

查看试题解析
17. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴是x＝1，下列结论：①abc＞0；② $b^{2} - 4 a c > 0$ ；③8a+c＜0；④5a+b+2c＞0，正确的有（填序号）.

查看试题解析

三、解答题

18. 计算：

(1)、 $| - 3 | + \sqrt{3} \cdot \tan 30^{\circ} - \sqrt[3]{8} - {(2018 - π)}^{0} + {(\frac{1}{2})}^{- 1}$ ．

(2)、解方程： $\frac{1}{x - 2} + 2 = \frac{1 - x}{2 - x}$ ．

查看试题解析
19. 某市对市民开展了有关雾霾的调查问卷，调查内容是“你认为哪种治理雾霾措施最有效”，有以下四个选项：
A.绿化造林；B.汽车限行；C.禁止城市周边燃烧秸秆；D.使用环保能源．

调查过程随机抽取了部分市民进行调查，并将调查结果绘制了如图所示的条形统计图和扇形统计图．

请根据图中的信息回答下列问题：

(1)、求这次被调查的市民人数．

(2)、求统计图中D所对应的百分比．

(3)、估计该市240000名市民中认同“汽车限行”的人数．

查看试题解析
20. 已知，如图，四边形ABCD的对角线AC⊥BD于点E ，点F为四边形ABCD外一点，且∠FCA＝90°，BC平分∠DBF ， ∠CBF＝∠DCB ．求证：四边形DBFC是菱形．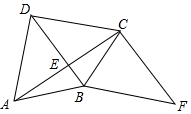

查看试题解析
21. 为做好延迟开学期间学生的在线学习服务工作，市教育局推出“中小学延迟开学期间网络课堂”，为学生提供线上学习，据统计，第一批公益课受益学生20万人次，第三批公益课受益学生24.2万人次．

(1)、如果第二批，第三批公益课受益学生人次的增长率相同，求这个增长率；

(2)、按照这个增长率，预计第四批公益课受益学生将达到多少万人次？

查看试题解析
22. 如图所示，某数学活动小组选定测量小河对岸树BC的高度，他们在斜坡上D处测得树顶端B的仰角是30°，从D处朝树方向下坡走2米到达坡底A处，在A处测得树顶端B的仰角是48°，若坡AF的坡度i＝1： $\sqrt{3}$ ，求树的高度．（结果保留整数，参考数据：sin48°≈0.7，cos48°≈0.7，tan48°≈1.1， $\sqrt{3} \approx$ 1.7）

查看试题解析
23. 如图，已知∠AOB=90°，∠OAB=30°，反比例函数 $y = - \frac{3}{x} (x < 0)$ 的图象过点 $B (- 3 ， a)$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象过点A.

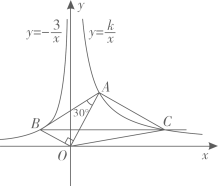(1)、求 $a$ 和 $k$ 的值.

(2)、过点B作BC∥x轴，与双曲线 $y = \frac{k}{x}$ 交于点C.求△OAC的面积.

查看试题解析
24. 如图，已知AB是 $⊙ O$ 的直径，直线BC与 $⊙ O$ 相切于点B，过点A作AD//OC交 $⊙ O$ 于点D，连接CD.

(1)、求证：CD是 $⊙ O$ 的切线.

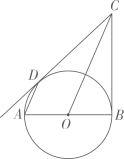(2)、若 $A D = 4$ ，直径 $A B = 12$ ，求线段BC的长.

查看试题解析
25. 如图，抛物线y＝ax²＋bx＋4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C ．连接AC ， BC ，点P是第一象限内抛物线上的一个动点，点P的横坐标为m ．

(1)、求此抛物线的表达式；

(2)、过点P作PN⊥BC ，垂足为点N ，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？

(3)、若抛物线上有且仅有三个点M₁、M₂、M₃ ，使得△M₁BC、△M₂BC、△M₃BC的面积均为定值S ，求出满足条件的定值S ．

查看试题解析