山东省济南市天桥区2021年中考数学二模试卷
试卷更新日期:2021-06-16 类型:中考模拟
一、单选题
-
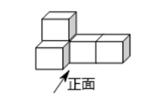
1. -5的绝对值等于( )A、-5 B、5 C、 D、2. 如图是由五个相同的小立方块搭成的几何体,这个几何体的俯视图是( )
 A、
A、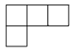 B、
B、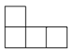 C、
C、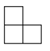 D、
D、 3. 数据697800用科学记数法表示为( )A、697.8×103 B、69.78×104 C、6.978×105 D、0.6978×1064. 如图,AB∥CD , EF分别与AB , CD交于点B , F . 若∠E=20°,∠EFC=130°,则∠A的度数是( )
3. 数据697800用科学记数法表示为( )A、697.8×103 B、69.78×104 C、6.978×105 D、0.6978×1064. 如图,AB∥CD , EF分别与AB , CD交于点B , F . 若∠E=20°,∠EFC=130°,则∠A的度数是( ) A、20° B、30° C、40° D、50°5. 下列地铁标志图形中,既是轴对称图形又是中心对称图形的是( )A、
A、20° B、30° C、40° D、50°5. 下列地铁标志图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 化简 的结果为( )A、 B、 C、 D、7. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:
6. 化简 的结果为( )A、 B、 C、 D、7. 为调动学生参与体育锻炼的积极性,某校组织了一分钟跳绳比赛活动,体育组随机抽取了10名参赛学生的成绩,将这组数据整理后制成统计表:一分钟跳绳个数(个)
141
144
145
146
学生人数(名)
5
2
1
2
则关于这组数据的结论正确的是( )
A、平均数是144 B、众数是141 C、中位数是144.5 D、方差是5.48. 若点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )A、y1>y2>y3 B、y3>y2>y1 C、y2>y1>y3 D、y1>y3>y29. 如图,△ABC的顶点坐标分别为A(4,6)、B(5,2)、C(2,1),如果将△ABC绕点C按逆时针方向旋转90°,后再向下平移5个单位,得到△A′B′C , 那么点A′的坐标是( ) A、(-3,-2) B、(3,-8) C、(-2,-1) D、(1,-1)10. 如图,Rt△ABC中,∠C=90°,用尺规分别截取BE , BD , 使BE=BD , 分别以D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为( )
A、(-3,-2) B、(3,-8) C、(-2,-1) D、(1,-1)10. 如图,Rt△ABC中,∠C=90°,用尺规分别截取BE , BD , 使BE=BD , 分别以D、E为圆心、以大于 的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G . 若CG=1,P为AB上一动点,则GP的最小值为( ) A、无法确定 B、 C、1 D、211. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)
A、无法确定 B、 C、1 D、211. 小明使用测角仪在甲楼底端A处测得熊猫C处的仰角为53°,在甲楼B处测得熊猫C处的仰角 已知AB=4.5米,则熊猫C处距离地面AD的高度为( )(参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33) A、13.6 B、18.1 C、17.3 D、16.812. 关于二次函数 的三个结论:①对任意实数m,都有 与 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则 或 ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则 或 .其中正确的结论是( )A、①② B、①③ C、②③ D、①②③
A、13.6 B、18.1 C、17.3 D、16.812. 关于二次函数 的三个结论:①对任意实数m,都有 与 对应的函数值相等;②若3≤x≤4,对应的y的整数值有4个,则 或 ;③若抛物线与x轴交于不同两点A,B,且AB≤6,则 或 .其中正确的结论是( )A、①② B、①③ C、②③ D、①②③二、填空题
-
13. 分解因式: ;14. 一个不透明的口袋中装有2个红球和若干个白球,它们除颜色外其它完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在20%附近,口袋中白球最有可能有个;15. 若代数式 与x-3互为相反数,则x=;16. 如图,已知正六边形的边长为4,分别以正六边形的6个顶点为圆心作半径是2的圆,则图中阴影部分的面积为.
 17. 甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到B地后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间(x小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为小时.
17. 甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均在同一路线上匀速行驶,乙到B地后即停车等甲,甲、乙两人之间的距离y(千米)与甲行驶的时间(x小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为小时.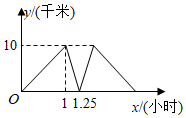 18. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是.
18. 如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且AF= BE,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②△AEG的周长为(1+ )a;③BE2+DG2=EG2;④△EAF的面积的最大值是 a2;⑤当时BE= a,G是线段AD的中点.其中正确的结论是.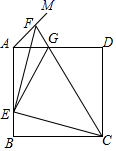
三、解答题
-
19. 计算:20. 解不等式组21. 如图,在矩形ABCD中,对角线AC , BD相交于点O , AE⊥BD于点E , DF⊥AC于点F . 求证:AE=DF .
 22. 某校政治实践小组就近期人们比较关注的五个话题:“A.5G通讯;B.民法典;C.北斗导航;D.数字经济;E . 小康社会”,对学生进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.
22. 某校政治实践小组就近期人们比较关注的五个话题:“A.5G通讯;B.民法典;C.北斗导航;D.数字经济;E . 小康社会”,对学生进行了随机抽样调查,每人只能从中选择一个本人最关注的话题,根据调查结果绘制了如图两幅不完整的统计图.请结合统计图中的信息,解决下列问题:
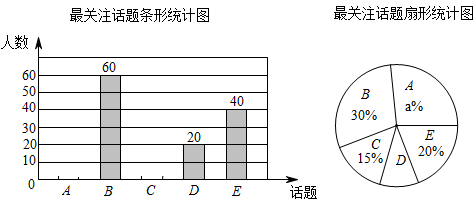 (1)、政治实践小组在这次活动中,调查的学生共有人;(2)、将图中的最关注话题条形统计图补充完整;(3)、政治实践小组进行专题讨论中,甲、乙两个小组从三个话题:“A.5G通讯;B.民法典;C.北斗导航”中抽签(不放回)选一项进行发言,利用树状图或表格,求出两个小组选择A、B话题发言的概率.23. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD , OP与AB的延长线交于点P , 过点B的切线交OP于点C .
(1)、政治实践小组在这次活动中,调查的学生共有人;(2)、将图中的最关注话题条形统计图补充完整;(3)、政治实践小组进行专题讨论中,甲、乙两个小组从三个话题:“A.5G通讯;B.民法典;C.北斗导航”中抽签(不放回)选一项进行发言,利用树状图或表格,求出两个小组选择A、B话题发言的概率.23. 如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD , OP与AB的延长线交于点P , 过点B的切线交OP于点C . (1)、求证:∠CBP=∠ADB;(2)、若OA=6,AB=4,求线段BP的长.24. 越野自行车是中学生喜爱的交通工具,市场巨大,竞争也激烈.某品牌经销商经营的A型车去年销售总额为50000元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少10000元.
(1)、求证:∠CBP=∠ADB;(2)、若OA=6,AB=4,求线段BP的长.24. 越野自行车是中学生喜爱的交通工具,市场巨大,竞争也激烈.某品牌经销商经营的A型车去年销售总额为50000元,今年每辆售价比去年降低400元,若卖出的数量相同,销售总额将比去年减少10000元.A , B两种型号车今年进货和销售价格表
A型车
B型车
进货价
1100元/辆
1400元辆
销售价
?元/辆
2000元/辆
(1)、今年A型车每辆售价为多少元?(2)、该品牌经销商计划新进一批A型车和新款B型车共60辆,且B型车的进货数量不超过A型车数量的2倍,请问应如何安排两种型号车的进货数量,才能使这批越野自行车售出后获利最多?25. 如图,直线 经过点A(-3,0)与y轴正半轴交于B , 在x轴正半轴上有一点D , 且tan 过D点作DC⊥x轴交直线 于C点,反比例函数 经过点C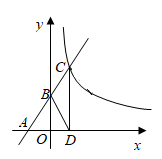 (1)、求b和反比例函数的解析式(2)、将点B向右平移m个单位长度得到点P , 当四边形BCPD为菱形时,求出m的值,并判断点P是否落在反比例函数图象上.(3)、点E是x轴上一点,且△COE是等腰三角形,求所有点E的坐标.26. 如图1,在△ABC中,AB=AC=2,∠BAC=90°,点P为BC边的中点,直线a经过点A , 过B作BE⊥a , 垂足为E , 过C作CF⊥a , 垂足为F , 连接PE、PF .
(1)、求b和反比例函数的解析式(2)、将点B向右平移m个单位长度得到点P , 当四边形BCPD为菱形时,求出m的值,并判断点P是否落在反比例函数图象上.(3)、点E是x轴上一点,且△COE是等腰三角形,求所有点E的坐标.26. 如图1,在△ABC中,AB=AC=2,∠BAC=90°,点P为BC边的中点,直线a经过点A , 过B作BE⊥a , 垂足为E , 过C作CF⊥a , 垂足为F , 连接PE、PF . (1)、当点B、P在直线a的异侧时,延长EP交CF于点G , 猜想线段PF和EG的数量关系为;(2)、如图2,直线a绕点A旋转,当点BP在直线a的同侧时,若(1)中其它条件不变,(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)、直线a绕点A旋转一周的过程中,当线段PF的长度最大时,请判断四边形BEFC的形状,并求出它的面积.27. 如图,抛物线 与x轴交于A、B两点(B在A的右侧),且与直线y=x+2交于A、C两点,已知B点的坐标为(6,0).
(1)、当点B、P在直线a的异侧时,延长EP交CF于点G , 猜想线段PF和EG的数量关系为;(2)、如图2,直线a绕点A旋转,当点BP在直线a的同侧时,若(1)中其它条件不变,(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)、直线a绕点A旋转一周的过程中,当线段PF的长度最大时,请判断四边形BEFC的形状,并求出它的面积.27. 如图,抛物线 与x轴交于A、B两点(B在A的右侧),且与直线y=x+2交于A、C两点,已知B点的坐标为(6,0).
 (1)、求抛物线的函数表达式;(2)、点E是线段AC上一点,且满足 ,
(1)、求抛物线的函数表达式;(2)、点E是线段AC上一点,且满足 ,①若点P为直线AC上方抛物线上一动点,设点P的横坐标为t , 当t为何值时,△PEA的面积最大;
②过点E向x轴作垂线,交x轴于点F , 在抛物线上是否存在一点N , 使得∠NAC=∠FEB , 若存在,直接写出点N的坐标,若不存在,请说明理由.