山东省淄博市2021届高三数学三模试卷

试卷更新日期：2021-06-16 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $A = {x | 1 - \frac{2}{x} < 0}$ ， $B = {x | | x | \leq 1}$ ，则如图阴影部分表示的集合是（）

A、 $[- 1 ， 0)$ B、 $[- 1 ， 0) \cup [1 ， 2)$ C、 $(1 ， 2)$ D、 $(0 ， 1)$

查看试题解析
2. 某个国家某种病毒传播的中期，感染人数 $y$ 和时间 $x$ （单位：天）在 $18$ 天里的散点图如图所示，下面四个回归方程类型中最适宜作为感染人数 $y$ 和时间 $x$ 的回归方程类型的是（）

A、 $y = a + b x$ B、 $y = a + b e^{x}$ C、 $y = a + b \ln x$ D、 $y = a + b \sqrt{x}$

查看试题解析
3. 在正项等比数列 ${a_{n}}$ 中，若 $a_{2021}$ 是 $a_{2019}$ ， $a_{2020}$ 两项的等差中项，则 $q =$ （）

A、1 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、-1

查看试题解析
4. 已知向量 $\vec{a}$ 、 $\vec{b}$ 满足 $| \vec{a} | = | \vec{b} | = | \vec{a} - \vec{b} | = 1$ ，则 $| 2 \vec{a} + \vec{b} | =$ （）

A、3 B、 $\sqrt{3}$ C、7 D、 $\sqrt{7}$

查看试题解析
5. 已知 $z \in C$ ，且 $| z - i | = 1$ ， $i$ 为虚数单位，则 $| z - 1 |$ 的最大值是（）

A、2 B、 $\sqrt{2} + 1$ C、 $\sqrt{2} - 1$ D、 $\sqrt{2}$

查看试题解析
6. 已知锐角 $α$ 、 $β$ 满足 $α - β = \frac{π}{3}$ ，则 $\frac{1}{\cos α \cos β} + \frac{1}{\sin α \sin β}$ 的最小值为（）

A、4 B、 $4 \sqrt{3}$ C、8 D、 $8 \sqrt{3}$

查看试题解析
7. 算盘是一种手动操作计算辅助工具．它起源于中国，迄今已有2600多年的历史，是中国古代的一项重要发明，算盘有很多种类．现有一种算盘（如图一），共两档，自右向左分别表示个位和十位，档中横以梁，梁上一珠拨下，记作数字5，梁下四珠，上拨每珠记作数字1（例如图二中算盘表示整数51）．如果拨动图一算盘中的三枚算珠，可以表示不同整数的个数为（）

A、16 B、15 C、12 D、10

查看试题解析
8. 设双曲线 $C ： \frac{x^{2}}{9} - \frac{y^{2}}{16} = 1$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，点P（异于顶点）在双曲线C的右支上，则下列说法正确的是（）

A、 $△ P F_{1} F_{2}$ 可能是正三角形 B、P到两渐近线的距离之积是定值 C、若 $P F_{1} ⊥ P F_{2}$ ，则 $△ P F_{1} F_{2}$ 的面积为8 D、在 $△ P F_{1} F_{2}$ 中， $\frac{\sin ∠ F_{1} P F_{2}}{\sin ∠ P F_{2} F_{1} - \sin ∠ P F_{1} F_{2}} = \frac{5}{4}$

查看试题解析

二、多选题

9. 已知正四棱台的上底面边长为1，侧棱长为2，高为 $\sqrt{2}$ ，则（）

A、棱台的侧面积为 $8 \sqrt{3}$ B、棱台的体积为 $13 \sqrt{2}$ C、棱台的侧棱与底面所成的角 $\frac{π}{4}$ D、棱台的侧面与底面所成二面角的正弦值为 $\frac{\sqrt{3}}{3}$

查看试题解析
10. 下列说法正确的是（）

A、某高中为了解在校学生对参加某项社会实践活动的意向，拟采用分层抽样的方法从该校三个年级的学生中抽取一个容量为60的样本，已知该校高一、高二，高三年级学生之比为 $6 ： 5 ： 4$ ，则应从高二年级中抽取20名学生 B、线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ 对应的直线至少经过其样本数据点中的一个点 C、命题“ $\forall x > 0$ ， $\lg (x^{2} + 1) \geq 0$ ”的否定是“ $\exists x > 0$ ， $\lg (x^{2} + 1) < 0$ " D、方差描述了一组数据围绕平均数波动的大小，方差越大，数据的离散程度越大，方差越小，数据的离散程度越小

查看试题解析
11. 已知圆 $O_{1} ： x^{2} + y^{2} - 2 x - 3 = 0$ 和圆 $O_{2} ： x^{2} + y^{2} - 2 y - 1 = 0$ 的交点为 $A$ ， $B$ ，则（）

A、圆 $O_{1}$ 和圆 $O_{2}$ 有两条公切线 B、直线 $A B$ 的方程为 $x - y + 1 = 0$ C、圆 $O_{2}$ 上存在两点 $P$ 和 $Q$ 使得 $| P Q | > | A B |$ D、圆 $O_{1}$ 上的点到直线 $A B$ 的最大距离为 $2 + \sqrt{2}$

查看试题解析
12. 2021年3月30日，小米正式开始启用具备“超椭圆”数学之美的新 $l o g o$ ．设计师的灵感来源于曲线 $C ： {| x |}^{n} + {| y |}^{n} = 1$ ．则下列说法正确的是（）

A、曲线 $C$ 关于原点成中心对称 B、当 $n = - 2$ 时，曲线 $C$ 上的点到原点的距离的最小值为2 C、当 $n > 0$ 时，曲线 $C$ 所围成图形的面积的最小值为 $π$ D、当 $n > 0$ 时，曲线 $C$ 所围成图形的面积小于4

查看试题解析

三、填空题

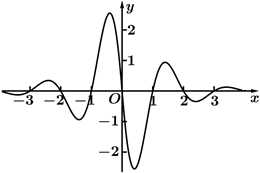
13. 请写出一个函数 $f (x) =$ ，使之同时具有如下性质：① $\forall x \in R$ ， $f (x) = f (4 - x)$ ，② $\forall x \in R$ ， $f (x + 4) = f (x)$ .

查看试题解析
14. 已知椭圆C的左､右焦点分别为 $F_{1} ， F_{2}$ ，直线AB过 $F_{1}$ 与椭圆交于A ， B两点，当 $△ F_{2} A B$ 为正三角形时，该椭圆的离心率为.

查看试题解析
15. 已知函数 $f (x) = \frac{4 \cos (ω x + φ)}{e^{| x |}}$ （ $ω > 0$ ， $0 < φ < π$ ）的部分图像如图所示，则 $ω + φ =$ ．

查看试题解析
16. 如图，在 $3 \times 3$ 的点阵中，依次随机地选出 $A$ 、 $B$ 、 $C$ 三个点，则选出的三点满足 $\vec{A B} \cdot \vec{A C} < 0$ 的概率是．

查看试题解析

四、解答题

17. $△ A B C$ 的内角 $A$ 、 $B$ ， $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ， $\cos (\frac{π}{3} - B) \cdot \sin (\frac{π}{6} + B) = \frac{3}{4}$ ， $a + c = 2$ ．

(1)、求角 $B$ 的大小；

(2)、求 $△ A B C$ 外接圆面积的最小值．

查看试题解析
18. 在图1所示的平面图形 $A B C D$ 中， $△ A B D$ 是边长为4的等边三角形， $B D$ 是 $∠ A D C$ 的平分线，且 $B D ⊥ B C$ ， $M$ 为 $A D$ 的中点，以 $B M$ 为折痕将 $△ A B M$ 折起得到四棱锥 $A - B C D M$ （如图2）．

(1)、设平面 $A B C$ 和 $A D M$ 的交线为 $l$ ，在四棱雉 $A - B C D M$ 的棱 $A C$ 上求一点 $N$ ，使直线 $B N // l$ ；

(2)、若二面角 $A - B M - D$ 的大小为 $60 °$ ，求平面 $A B D$ 和 $A C D$ 所成锐二面角的余弦值．

查看试题解析
19. 某电台举办有奖知识竞答比赛，选手答题规则相同.甲每道题自己有把握独立答对的概率为 $\frac{1}{2}$ ，若甲自己没有把握答对，则在规定时间内连线亲友团寻求帮助，其亲友团每道题能答对的概率为p ，假设每道题答对与否互不影响.

(1)、当 $p = \frac{1}{5}$ 时，
（i）若甲答对了某道题，求该题是甲自己答对的概率；

（ii）甲答了4道题，计甲答对题目的个数为随机变量X ，求随机变量X的分布列和数学期望 $E X$ ；

(2)、乙答对每道题的概率为 $\frac{2}{3}$ (含亲友团)，现甲乙两人各答两个问题，若甲答对题目的个数比乙答对题目的个数多的概率不低于 $\frac{15}{36}$ ，求甲的亲友团每道题答对的概率p的最小值.

查看试题解析
20. 已知函数 $f (x) = \frac{\sin x}{x} (x > 0)$ ．

(1)、判断函数 $f (x)$ 在 $(0 ， π)$ 上的单调性；

(2)、证明函数 $f (x)$ 在 $(π ， 2 π)$ 内存在唯一的极值点 $x_{0}$ ，且 $f (x_{0}) < - \frac{2}{3 π}$ ．

查看试题解析
21. 若存在常数 $m \in R$ ，使得对于任意 $n \in N^{*}$ ，都有 $a_{n + 1} \geq m a_{n}$ ，则称数列 ${a_{n}}$ 为 $Z (m)$ 数列.

(1)、已知数列 ${a_{n}}$ 是公差为 $2$ 的等差数列，其前 $n$ 项和为 $S_{n}$ ，若 $S_{n}$ 为 $Z (1)$ 数列，求 $a_{1}$ 的取值范围；

(2)、已知数列 ${b_{n}}$ 的各项均为正数，记 ${b_{n}}$ 的前 $n$ 项和为 $R_{n}$ ，数列 ${b_{n}^{2}}$ 的前 $n$ 项和为 $T_{n}$ ，且 $3 T_{n} = R_{n}^{2} + 4 R_{n}$ ， $n \in N^{*}$ ，若数列 ${c_{n}}$ 满足 $c_{n} = b_{n} + \frac{1}{b_{n}}$ ，且 ${c_{n}}$ 为 $Z (m)$ 数列，求 $m$ 的最大值；

(3)、已知正项数列 ${d_{n}}$ 满足： $d_{n} \leq d_{n + 1} (n \in N^{*})$ ，且数列 ${d_{2 k - 1} d_{2 k + 1}}$ 为 $Z (r)$ 数列，数列 ${\frac{1}{d_{2 k} d_{2 k + 2}}}$ 为 $Z (s)$ 数列，若 $\frac{d_{2}}{d_{1}} = r s$ ，求证：数列 ${d_{n}}$ 中必存在无穷多项可以组成等比数列.

查看试题解析