海南省2021届高三下学期数学体艺生模拟考试试卷
试卷更新日期:2021-06-16 类型:高考模拟
一、单选题
-
1. 已知集合 , ,则 ( )A、{3} B、{5} C、 D、2. 复数 在复平面内对应的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 设 为实数,则“ ”是“ ”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件4. 下列函数中,既是奇函数又在区间 上单调递减的是( )A、 B、 C、 D、5. 如图是某校高三某班甲、乙两位同学前六次模拟考试的数学成绩,则下列判断正确的是( )
 A、 ,甲比乙成绩稳定 B、 ,乙比甲成绩稳定 C、 ,甲比乙成绩稳定 D、 ,乙比甲成绩稳定6. 已知三棱锥 所有顶点都在球 的球面上,且 平面 ,若 , ,则球 的表面积为( )A、 B、5π C、4π D、7. 下列函数中,既是偶函数又存在零点的是( )A、y=lnx B、 C、y=sinx D、y=cosx8. 若等比数列 各项都是正数, , ,则 的值为( )A、42 B、63 C、84 D、168
A、 ,甲比乙成绩稳定 B、 ,乙比甲成绩稳定 C、 ,甲比乙成绩稳定 D、 ,乙比甲成绩稳定6. 已知三棱锥 所有顶点都在球 的球面上,且 平面 ,若 , ,则球 的表面积为( )A、 B、5π C、4π D、7. 下列函数中,既是偶函数又存在零点的是( )A、y=lnx B、 C、y=sinx D、y=cosx8. 若等比数列 各项都是正数, , ,则 的值为( )A、42 B、63 C、84 D、168二、多选题
-
9. 学校为了解新课程标准中提升阅读要求对学生阅读兴趣的影响情况,随机抽取100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示.将阅读时间不低于 的学生称为阅读霸,则下列结果正确的是( )
 A、抽样表明,该校约有一半学生为阅读霸 B、抽取的100名学生中有50名学生为阅读霸 C、该校学生中有50名学生不是阅读霸 D、抽样表明,该校有50名学生为阅读霸10. 如图,在长方体 中, , ,M、N分别为棱 , 的中点,则下列说法正确的是( )
A、抽样表明,该校约有一半学生为阅读霸 B、抽取的100名学生中有50名学生为阅读霸 C、该校学生中有50名学生不是阅读霸 D、抽样表明,该校有50名学生为阅读霸10. 如图,在长方体 中, , ,M、N分别为棱 , 的中点,则下列说法正确的是( ) A、A、M、N、B四点共面 B、平面 平面 C、 与BN所成角 D、 平面ADM11. 已知双曲线C: 的左、右焦点分别为 , ,则能使双曲线C的方程为 的是( )A、离心率为 B、双曲线过点 C、渐近线方程为 D、实轴长为412. 将函数 的图象向左平移 个单位长度,再向上平移1个单位长度,得到函数 的图象,则下列关于函数 的说法正确的是( )A、最大值为 ,图象关于直线 对称 B、图象关于y轴对称 C、最小正周期为 D、图象关于点 对称
A、A、M、N、B四点共面 B、平面 平面 C、 与BN所成角 D、 平面ADM11. 已知双曲线C: 的左、右焦点分别为 , ,则能使双曲线C的方程为 的是( )A、离心率为 B、双曲线过点 C、渐近线方程为 D、实轴长为412. 将函数 的图象向左平移 个单位长度,再向上平移1个单位长度,得到函数 的图象,则下列关于函数 的说法正确的是( )A、最大值为 ,图象关于直线 对称 B、图象关于y轴对称 C、最小正周期为 D、图象关于点 对称三、填空题
-
13. 曲线 : 在点 处的切线方程为 .14. 已知向量 和 的夹角为 ,且 , ,则 .15. 展开式中的常数项为.16. 若 , ,且 ,则 的最小值是 , 当且仅当时,取得最值.
四、解答题
-
17. 在① ,② ,③ 这三个条件中任选一个,补充在下面问题中,若问题中的三角形存在,求 的值;若问题中的三角形不存在,说明理由.
问题:是否存在 ,它的内角 的对边分别为 ,且 , , ▲ ?
注:如果选择多个条件分别解答,按第一个解答计分.
18. 已知公比大于 的等比数列 满足 .(1)、求 的通项公式;(2)、求 .19. 如图,在三棱锥 中,平面 平面 , 和 均是等腰直角三角形, , , 、 分别为 、 的中点.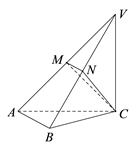
(Ⅰ)求证: 平面 ;
(Ⅱ)求证: ;
(Ⅲ)求直线 与平面 所成角的正弦值.
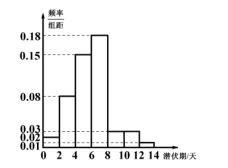
20. 目前,新冠病毒引发的肺炎疫情在全球肆虐,为了解新冠肺炎传播途径,采取有效防控措施,某医院组织专家统计了该地区500名患者新冠病毒潜伏期的相关信息,数据经过汇总整理得到如下图所示的频率分布直方图(用频率作为概率).潜伏期不高于平均数的患者,称为“短潜伏者”,潜伏期高于平均数的患者,称为“长潜伏者”.短潜伏者
长潜伏者
合计
60岁及以上
90
60岁以下
140
合计
300
附表及公式:
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)、求这500名患者潜伏期的平均数(同一组中的数据用该组区间的中点值作代表),并计算出这500名患者中“长潜伏者”的人数;(2)、为研究潜伏期与患者年龄的关系,以潜伏期是否高于平均数为标准进行分层抽样,从上述500名患者中抽取300人,得到如下列联表,请将列联表补充完整,并根据列联表判断是否有97.5%的把握认为潜伏期长短与患者年龄有关:(3)、研究发现,有5种药物对新冠病毒有一定的抑制作用,其中有2种特别有效,现在要通过逐一试验直到把这2种特别有效的药物找出来为止,每一次试验花费的费用是500元,设所需要的试验费用为X,求X的分布列与数学期望.