云南省大理下关教育集团2020-2021学年高一下学期数学期中考试试卷
试卷更新日期:2021-06-15 类型:期中考试
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
-
1. 已知集合 , ,则 ( )A、 B、 C、 D、2. 下列结论不正确的是( )A、若 , ,则 B、若 ,则 C、若 ,则 D、若 , ,则3. 已知复数 满足 ,则复数 的虚部为( )A、 B、 C、 D、4. 一元二次方程 ( )有一个正根和一个负根的充分不必要条件是( )A、 B、 C、 D、5. 已知 , , ,则 , , 的大小关系为( )A、 B、 C、 D、6. 如图,在正方体 中, , , 分别是 , , 的中点,则下列命题正确的是( )
 A、 B、 C、 平面 D、 平面7. 函数 的图象大致为( )A、
A、 B、 C、 平面 D、 平面7. 函数 的图象大致为( )A、 B、
B、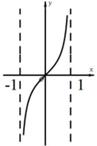 C、
C、 D、
D、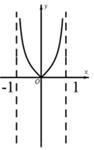 8. 函数 的最小正周期为( )A、 B、 C、 D、9. 在 中, , , ,则直线 通过 的( )A、垂心 B、外心 C、重心 D、内心10. 《掷铁饼者》取材于古希腊的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂及肩近似看成一张“弓”掷铁饼者的肩宽约为 米,一只手臂长约为 米(两臂等长),“弓”所在圆的半径约为 米,则掷铁饼者双手之间的直线距离约为( )
8. 函数 的最小正周期为( )A、 B、 C、 D、9. 在 中, , , ,则直线 通过 的( )A、垂心 B、外心 C、重心 D、内心10. 《掷铁饼者》取材于古希腊的体育竞技活动,刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间.现在把掷铁饼者张开的双臂及肩近似看成一张“弓”掷铁饼者的肩宽约为 米,一只手臂长约为 米(两臂等长),“弓”所在圆的半径约为 米,则掷铁饼者双手之间的直线距离约为( ) A、 米 B、 米 C、 米 D、 米11. 若向量 , 是不共线的两个向量, 与 共线,当 时, 的最小值为( )A、4 B、2 C、 D、12. 已知函数是 上偶函数,且对于 都有 成立,当 , ,且 时,都有 .对于下列叙述;
A、 米 B、 米 C、 米 D、 米11. 若向量 , 是不共线的两个向量, 与 共线,当 时, 的最小值为( )A、4 B、2 C、 D、12. 已知函数是 上偶函数,且对于 都有 成立,当 , ,且 时,都有 .对于下列叙述;① ;
②直线 是函数 的一条对称轴;
③函数 在区间 上为增函数;
④函数 在区间 上有四个零点.其中正确命题的序号是( )
A、①②③ B、①② C、②④ D、①②④二、填空题:本大题共4个小题,每小题5分,共20分。
-
13. 已知 是任意角,且满足 ,则常数 的一个取值为 .14. 将一个直角边长为1的等腰直角三角形绕其一条直角边旋转一周所形成几何体的体积为 .15. 在山顶铁塔上 处测得地面上一点 的俯角 ,在塔底 处测得点 的俯角 ,已知铁塔 部分高32米,山高 .
 16. 已知定义在 上的函数 满足 且 ,函数 的表达式为 ,则方程 在区间 上的所有实数根之和为 .
16. 已知定义在 上的函数 满足 且 ,函数 的表达式为 ,则方程 在区间 上的所有实数根之和为 .三、解答题:解答应写出文字说明,证明过程或演算步骤,共70分。
-
17. 向量 ,(1)、求向量 的模长;(2)、若向量 ,且 ,求实数 的值.18. 若向量 , ,设函数(1)、求 在 上的单调增区间;(2)、在角 为锐角的 中,角 、 、 的对边分别为 、 、 , 且 的面积为3, ,求 的值.19. 某生物研究者于元旦在湖中放入一些凤眼莲(其覆盖面积为 ),这些凤眼莲在湖中的蔓延速度越来越快,二月底测得凤眼莲的覆盖面积为 ,三月底测得凤眼莲的覆盖面积为 ,凤眼莲的覆盖面积 (单位: )与月份 (单位:月)的关系有两个函数模型 ( , )与 ( , )可供选择。(1)、试判断哪个函数模型更合适并求出该模型的解析式;(2)、求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据: , ).20. 已知 内角 、 、 所对的边分别为 、 、 ,A为锐角,在以下三个条件中任选一个:① ;② ;③ ;并解答以下问题:(1)、若选 ▲ (填序号),求 的值;(2)、在(1)的条件下,若 ,求 面积 的最大值.
