天津市河东区一片区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
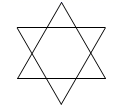
1. 计算﹣22的结果等于( )A、﹣2 B、﹣4 C、2 D、42. 的值等于( )A、1 B、 C、 D、3. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、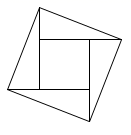 C、
C、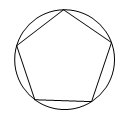 D、
D、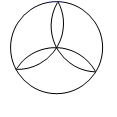 4. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点于距离地球36002公里的地球同步轨道.将36000用科学记数法表示应为( )A、 B、 C、 D、5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
4. 2020年6月23日,北斗三号最后一颗全球组网卫星从西昌卫星发射中心发射升空,6月30日成功定点于距离地球36002公里的地球同步轨道.将36000用科学记数法表示应为( )A、 B、 C、 D、5. 如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )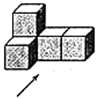 A、
A、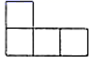 B、
B、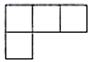 C、
C、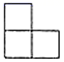 D、
D、 6. 估计 的值在( )A、7到8之间 B、8到9之间 C、9到10之间 D、9到10之间或 到 之间7. 计算 的结果为( )A、 B、 C、 D、8. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为4的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
6. 估计 的值在( )A、7到8之间 B、8到9之间 C、9到10之间 D、9到10之间或 到 之间7. 计算 的结果为( )A、 B、 C、 D、8. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为4的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )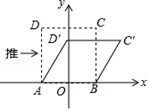 A、( ,2) B、(4,1) C、(4, ) D、(4, )9. 方程组 的解是( )A、 B、 C、 D、10. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
A、( ,2) B、(4,1) C、(4, ) D、(4, )9. 方程组 的解是( )A、 B、 C、 D、10. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( ) A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等12. 表中所列x、y的7对值是二次函数 图象上的点所对应的坐标,
A、AE=EF B、AB=2DE C、△ADF和△ADE的面积相等 D、△ADE和△FDE的面积相等12. 表中所列x、y的7对值是二次函数 图象上的点所对应的坐标,其中
x
…
…
y
…
6
m
11
k
11
m
6
…
根据表中提供约信息,有以下4个判断:
① ;② ;③当 时,y的值是k;④ ;其中正确结论的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
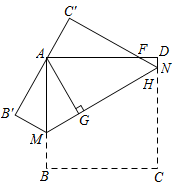
13. .14. 计算: .15. 不透明袋子中装有6个球,其中有1个红球、2个绿球和3个黑球,这些球除颜色外无其他差别,从袋子中随机取出1个球,则它是绿球的概率是 .16. 一次函数 的图象与x轴的交点坐标为.17. 如图,若该正方形ABCD边长为10,将正方形沿着直线MN翻折,使得BC的对应边 恰好经过点A , 过点A作 ,垂足分别为G , 若 ,则 的长度为 .
三、解答题
-
18. 如图,在每个小正方形的边长为 的网格中,点A,B,C在格点上,以点A为圆心、AC为半径的半圆交AB于点 E.
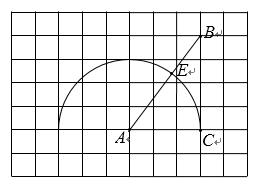 (1)、BE的长为;(2)、请用无刻度的直尺,在如图所示的网格中,找一点P(点P,C 在AB两侧),使PA=5,PE与半圆相切. 简要说明点P的位置是如何找到的.19. 解不等式组: 请结合题意填空,完成本题的解答:(1)、解不等式①,得: ;(2)、解不等式②,得: ;(3)、把不等式①和②的解集在数轴上表示出来;(4)、原不等式组的解集为: ;
(1)、BE的长为;(2)、请用无刻度的直尺,在如图所示的网格中,找一点P(点P,C 在AB两侧),使PA=5,PE与半圆相切. 简要说明点P的位置是如何找到的.19. 解不等式组: 请结合题意填空,完成本题的解答:(1)、解不等式①,得: ;(2)、解不等式②,得: ;(3)、把不等式①和②的解集在数轴上表示出来;(4)、原不等式组的解集为: ; 20. 某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:
20. 某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题: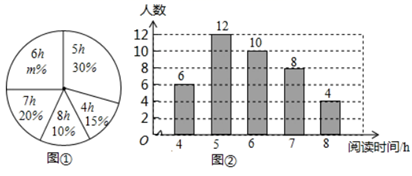 (1)、本次接受随机抽样调查的学生人数为 ,图①中 的值为;(2)、求本次调查获取的样本数据的众数、中位数和平均数;(3)、根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.21. 已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .
(1)、本次接受随机抽样调查的学生人数为 ,图①中 的值为;(2)、求本次调查获取的样本数据的众数、中位数和平均数;(3)、根据样本数据,估计该校一周的课外阅读时间大于 的学生人数.21. 已知AB为 的直径,EF切 于点D , 过点B作 于点H交 于点C , 连接BD .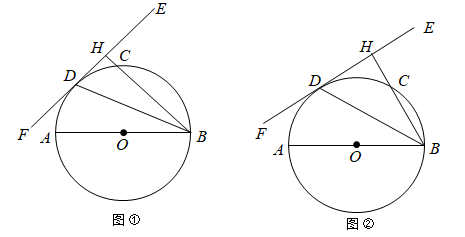 (1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.22. 如图,某教学楼AB的后面有一建筑物CD , 当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).
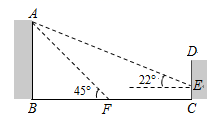
(1)、如图①,若 ,求 的大小;(2)、如图②,若C为弧BD的中点,求 的大小.22. 如图,某教学楼AB的后面有一建筑物CD , 当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45°时,教学楼顶A在地面上的影子F与墙角C的距离为18m (B、F、C在一条直线上).求教学楼AB的高度.(结果保留整数)
(参考数据:sin22° 0.37,cos22° 0.93,tan22° 0.40 .)
 23. 某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米,甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地,乙骑行到一半时,发现有东西忘带,立即返,拿好东西之后再从学校出发在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地.已知,乙骑行的总时间是甲步行时间的 ,设甲步行的时间为x(分),图中线段OA表示甲离开学校的路程y(米)与x(分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程y(米)与x(分)的函数关系的图像.根据图中所给的信息,解答下列问题:
23. 某学校甲、乙两名同学去爱国主义教育基地参观,该基地与学校相距2400米,甲从学校步行去基地,出发5分钟后乙再出发,乙从学校骑自行车到基地,乙骑行到一半时,发现有东西忘带,立即返,拿好东西之后再从学校出发在骑行过程中,乙的速度保持不变,最后甲、乙两人同时到达基地.已知,乙骑行的总时间是甲步行时间的 ,设甲步行的时间为x(分),图中线段OA表示甲离开学校的路程y(米)与x(分)的函数关系的图像.图中折线B—C—D和线段EA表示乙离开学校的路程y(米)与x(分)的函数关系的图像.根据图中所给的信息,解答下列问题: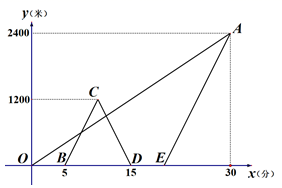 (1)、填表
(1)、填表甲离开学校的时间/分
5
10
15
20
30
乙离开学校的距离/米
(2)、填空①甲步行的速度是米/分,乙骑行的速度是米/分;
②在行进过程中,甲出发分钟后,甲、乙两人相遇?
(3)、若s(米)表示甲、乙两人之间的距离,当 时,求S(米)关于x(分)的函数关系式.24. 在平面直角坐标系中,O为原点,点A(﹣6,0)、点C(0,6),若正方形OABC绕点O顺时针旋转,得正方形OA′B′C′,记旋转角为α: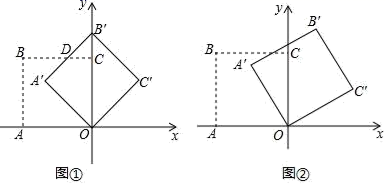 (1)、如图①,当α=45°时,求BC与A′B′的交点D的坐标;(2)、如图②,当α=60°时,求点B′的坐标;(3)、若P为线段BC′的中点,求AP长的取值范围(直接写出结果即可).25. 抛物线y=﹣x2+bx+c(b , c为常数)与x轴交于点(x1 , 0)和(x2 , 0),与y轴交于点A , 点E为抛物线顶点.
(1)、如图①,当α=45°时,求BC与A′B′的交点D的坐标;(2)、如图②,当α=60°时,求点B′的坐标;(3)、若P为线段BC′的中点,求AP长的取值范围(直接写出结果即可).25. 抛物线y=﹣x2+bx+c(b , c为常数)与x轴交于点(x1 , 0)和(x2 , 0),与y轴交于点A , 点E为抛物线顶点.(Ⅰ)当x1=﹣1,x2=3时,求点E , 点A的坐标;
(Ⅱ)①若顶点E在直线y=x上时,用含有b的代数式表示c;
②在①的前提下,当点A的位置最高时,求抛物线的解析式;
(Ⅲ)若x1=﹣1,b>0,当P(1,0)满足PA+PE值最小时,求b的值.