天津市和平区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 计算 的结果等于( )A、-6 B、0 C、16 D、62. 的值等于( )A、1 B、 C、2 D、3. 下列图案中,既是轴对称图形,又是中心对称图形的是( )A、
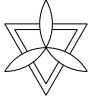 B、
B、 C、
C、 D、
D、 4. 2020年初,国家统计局发布数据,按现行国家农村贫困标准测算,截至2019年末,全国农村贫困人口减少至551万人,累计减少93480000人,将93480000用科学记数法表示为( )A、 B、 C、 D、5. 如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )
4. 2020年初,国家统计局发布数据,按现行国家农村贫困标准测算,截至2019年末,全国农村贫困人口减少至551万人,累计减少93480000人,将93480000用科学记数法表示为( )A、 B、 C、 D、5. 如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )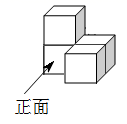 A、
A、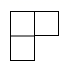 B、
B、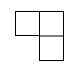 C、
C、 D、
D、 6. 估计 的值在( )A、7和8之间 B、6和7之间 C、5和6之间 D、4和5之间7. 方程组 的解是( )A、 B、 C、 D、8. 计算 的结果为( )A、3 B、-3 C、 D、9. 如图所示,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )
6. 估计 的值在( )A、7和8之间 B、6和7之间 C、5和6之间 D、4和5之间7. 方程组 的解是( )A、 B、 C、 D、8. 计算 的结果为( )A、3 B、-3 C、 D、9. 如图所示,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( ) A、(2,-3) B、(2,3) C、(3,2) D、(3,-2)10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,以点 为旋转中心,把 顺时针旋转得 .记旋转角为 ,连接AE, 为 ,则 的度数为( )
A、(2,-3) B、(2,3) C、(3,2) D、(3,-2)10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,以点 为旋转中心,把 顺时针旋转得 .记旋转角为 ,连接AE, 为 ,则 的度数为( )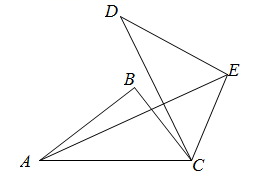 A、 B、 C、 D、12. 已知抛物线 ( 为常数, )的对称轴是直线 ,且与 轴、 轴分别交于 两点,其中点A在点 的右侧,直线 经过 两点.有下列结论:① ;② ;③ .其中正确的结论是( )A、① B、①② C、②③ D、①②③
A、 B、 C、 D、12. 已知抛物线 ( 为常数, )的对称轴是直线 ,且与 轴、 轴分别交于 两点,其中点A在点 的右侧,直线 经过 两点.有下列结论:① ;② ;③ .其中正确的结论是( )A、① B、①② C、②③ D、①②③二、填空题
-
13. 计算 的结果等于 .14. 计算 的结果等于 .15. 不透明袋子中装有12个球,其中有3个红球、4个黄球和5个绿球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是红球的概率是 .16. 直线 与 轴交点坐标为 .17. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=5,DA=5 ,则BD的长为 .
 18. 如图,在每个小正方形的边长为1的网格中,点A,点B,点D均在格点上,并且在同一个圆上,取格点M,连接AM并延长交圆于点C.
18. 如图,在每个小正方形的边长为1的网格中,点A,点B,点D均在格点上,并且在同一个圆上,取格点M,连接AM并延长交圆于点C.
(Ⅰ)四边形 外接圆的半径为 .
(Ⅱ)请在如图所示的网格中,用无刻度的直尺画出线段 ,使 平分 ,且点 在圆上,并简要说明点 的位置是如何找到的(不要求证明) .
三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(Ⅳ)原不等式组的解集为 ▲ .
20. 在一次“爱心助学”捐款活动中,全校同学人人拿出自己的零花钱,踊跃捐款,学生捐款额有5元、10元、15元、20元四种情况.李老师在全校范围内随机抽取部分学生,对捐款金额进行了统计,根据统计结果,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题: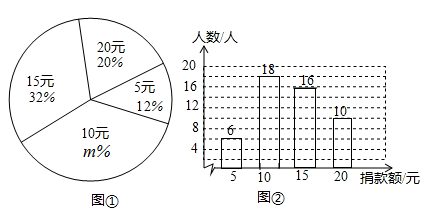 (1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.21. 已知 分别与 相切于点 ,延长 交直径 的延长线于点 .
(1)、本次抽取的学生人数为 ,图①中 的值为;(2)、求统计的这组学生捐款数据的平均数、众数和中位数;(3)、根据统计的学生捐款的样本数据,若该校共有800名初中学生,估计该校学生共捐款的钱数.21. 已知 分别与 相切于点 ,延长 交直径 的延长线于点 . (1)、如图①,若 ,求 的度数;(2)、如图②,在 上取一点 ,连接 ,当四边形 是平行四边形时,求 及 的大小.22. 如图, 两地之间有一座山,汽车原来从A地到B地需经C地沿折线 行驶,全长 .现开通隧道后,汽车直接沿直线AB行驶,已知 ,求隧道开通后,汽车从 地到 地的路程(结果精确到 ).参考数据: .
(1)、如图①,若 ,求 的度数;(2)、如图②,在 上取一点 ,连接 ,当四边形 是平行四边形时,求 及 的大小.22. 如图, 两地之间有一座山,汽车原来从A地到B地需经C地沿折线 行驶,全长 .现开通隧道后,汽车直接沿直线AB行驶,已知 ,求隧道开通后,汽车从 地到 地的路程(结果精确到 ).参考数据: . 23. 甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶.
23. 甲、乙两车从A城出发前往B城,在整个行程中,甲车离开A城的距离 与甲车离开A城的时间 的对应关系如图所示.乙车比甲车晚出发 ,以 的速度匀速行驶. (1)、填空:
(1)、填空:① 两城相距 ;
②当 时,甲车的速度为 ;
③乙车比甲车晚 到达 城;
④甲车出发 时,距离 城 ;
⑤甲、乙两车在行程中相遇时,甲车离开 城的时间为 ;
(2)、当 时,请直接写出 关于 的函数解析式.(3)、当 时,两车所在位置的距离最多相差多少 ?24. 如如图,将一个直角三角形纸片AOB , 放置在平面直角坐标系中,已知点O(0,0),点B在y轴的正半轴上, OA=2,∠ABO=90°,∠AOB=30°.D , E两点同时从原点O出发,D点以每秒 个单位长度的速度沿x轴正方向运动,E点以每秒1个单位长度的速度沿y轴正方向运动,连接DE , 交OA于点F , 将△OEF沿直线DE折叠得到△O′EF , 设D , E两点的运动时间为t秒.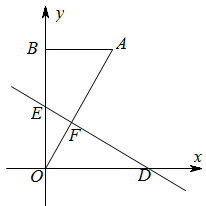 (1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,
(1)、求点 的坐标及 的度数;(2)、若折叠后 与 重叠部分的面积为 ,①当折叠后 与 重叠部分的图形为三角形时,请写出 与 的函数关系式,并直接写出 的取值范围;
②当重叠部分面积最大时,把 绕点 旋转,得到 ,点 的对应点分别为 ,连接 ,求 面积的最大值(直接写出结果即可).
25. 抛物线 过点 和点 ,与 轴交于点 ,顶点为点D.(Ⅰ)求点 的坐标;
(Ⅱ)点 是线段 上一动点,过点 作直线 轴,交抛物线于点 ,连接 并延长交 轴于点 ,连接 .若 的面积是 面积的2倍,求点 的坐标;
(Ⅲ)抛物线上一点 ,点 的横坐标是 ,连接 ,与 轴交于点 ,点 是线段 上一动点(不与点 ,点 重合)将 沿 所在直线翻折,得到 ,当 与 重叠部分的面积是 面积的 时,求线段 的长度.