天津市北辰区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 计算 的结果是( )A、-1 B、-2 C、2 D、152. 2cos 30°的值等于( )A、 1 B、 C、 D、23. 下列图案中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 中国首次火星探测任务命名为“天问一号”,在文昌航天发射场发射升空并成功进入预定轨道,截至2021年2月3日,“天问一号”探测器总飞行里程已超过449000000公里,将449000000用科学记数法表示应为( )A、 B、 C、 D、5. 如图是由6个相同的正方体组成的立体图形,它的主视图是( )
4. 中国首次火星探测任务命名为“天问一号”,在文昌航天发射场发射升空并成功进入预定轨道,截至2021年2月3日,“天问一号”探测器总飞行里程已超过449000000公里,将449000000用科学记数法表示应为( )A、 B、 C、 D、5. 如图是由6个相同的正方体组成的立体图形,它的主视图是( )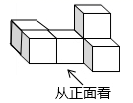 A、
A、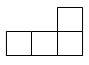 B、
B、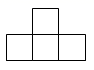 C、
C、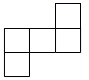 D、
D、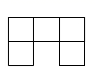 6. 估计 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 计算 的结果为( )A、1 B、x C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 如图,四边形 是矩形, , ,点 在第二象限,则点 的坐标是
6. 估计 的值在( )A、5和6之间 B、6和7之间 C、7和8之间 D、8和9之间7. 计算 的结果为( )A、1 B、x C、 D、8. 方程组 的解是( )A、 B、 C、 D、9. 如图,四边形 是矩形, , ,点 在第二象限,则点 的坐标是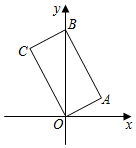 A、 B、 C、 D、10. 若点 , , 在反比例函数 的图象上,则 , , 的大小关系为( )A、 B、 C、 D、11. 如图,在平行四边形 中, , , , 是边 上任意一点,沿 剪开,将 沿 方向平移到 的位置,得到四边形 ,则四边形 周长的最小值为( )
A、 B、 C、 D、10. 若点 , , 在反比例函数 的图象上,则 , , 的大小关系为( )A、 B、 C、 D、11. 如图,在平行四边形 中, , , , 是边 上任意一点,沿 剪开,将 沿 方向平移到 的位置,得到四边形 ,则四边形 周长的最小值为( )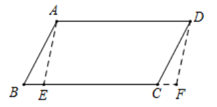 A、24 B、22 C、30 D、2812. 如图,抛物线 与 轴正半轴交于 , 两点,其中点 的坐标为 ,抛物线与 轴负半轴交于点 ,有下列结论:
A、24 B、22 C、30 D、2812. 如图,抛物线 与 轴正半轴交于 , 两点,其中点 的坐标为 ,抛物线与 轴负半轴交于点 ,有下列结论: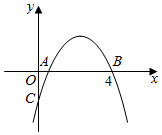
① ;② ;③若 与 是抛物线上两点,则 ;④若 ,则
其中,正确的结论是( )
A、①② B、③④ C、①④ D、②③二、填空题
-
13. 计算;x2·x5 的结果等于 .14. 计算 的结果等于.15. 不透明袋子中装有9个球,其中有4个红球,5个黑球,这些球除颜色外无其他差别.从袋子中随机取出l个球,则它是红球的概率是 .16. 直线y=2x+b(b为常数)的图象经过第一、三、四象限,则 的值可以是(写出一个即可).17. 如图,在长方形ABCD中,AB=3,BC=4,点E是边BC上的一点,连接AE,把∠B沿AE折叠,使点B落在点 处,当△CE 为直角三角形时,BE的长为 .
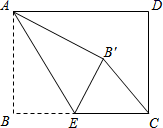 18. 如图,在每个小正方形的边长为1的网格中, 的顶点 , , 均落在格点上,以点 为圆心 长为半径的圆交 于点 .
18. 如图,在每个小正方形的边长为1的网格中, 的顶点 , , 均落在格点上,以点 为圆心 长为半径的圆交 于点 .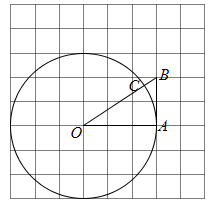
(Ⅰ)线段 的长等于;
(Ⅱ)若 切 于点 , 为 上的动点,当 取得最小值时,请用无刻度的直尺,在如图所示的网格中,画出点 , ,并简要说明点 , 的位置是如何找到的(不要求证明) .
三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ▲ ;
(Ⅱ)解不等式②,得 ▲ ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
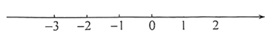
(Ⅳ)原不等式组的解集为 ▲ .
20. 某校为了解初中学生每周家务劳动的时间(单位: ),随机调查了该校部分初中学生,根据随机调查结果,绘制出如图的统计图①和图②请根据相关信息,解答下列问题: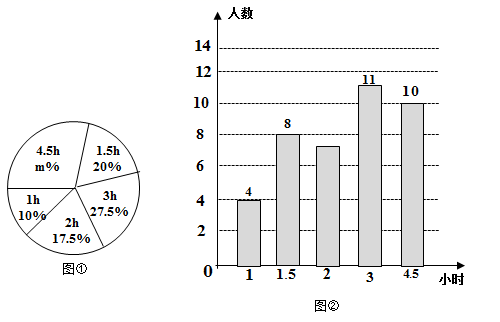
(Ⅰ)本次接受调查的初中生人数为 ▲ ,图①中 的值为 ▲
(Ⅱ)求统计的这组每周家务劳动时间数据的平均数、众数和中位数;
(Ⅲ)根据统计的这组每周家务劳动时间的样本数据,若该校共有900名初中生,估计该校每周在家劳动时间大于 的学生人数是多少.
21. 如图,在 中,直径 与弦 相交于点 , .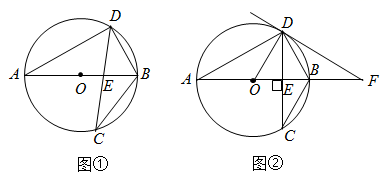
(Ⅰ)如图①,若 ,求 和 的大小;
(Ⅱ)如图②,若 ,过点 作 的切线 ,与 的延长线相交于点 .求 的大小.
22. 和平女神塑像是天津意大利风情区马可·波罗广场的标志性建筑.如图,在一次数学综合性实践活动中,小明为测量雕像 的高度,在点 处放置1.6米高的测角仪,从点 处测得雕像顶端 的仰角为31°,然后沿射线 方向前进7米到达点 处,又从点 处测得雕像顶端 的仰角为43°,点 , , , , , 在同一平面内,求雕像 的高度(结果精确到0.1)参考数据: , , , , , .
 23. 一个有进水管与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,12分钟后关闭进水管,放空容器中的水,每分钟的进水量和出水量是两个常数.容器内水量 (单位: )与时间 (单位: )之间的关系如图所示.
23. 一个有进水管与出水管的容器,从某时刻开始4分钟内只进水不出水,在随后的8分钟内既进水又出水,12分钟后关闭进水管,放空容器中的水,每分钟的进水量和出水量是两个常数.容器内水量 (单位: )与时间 (单位: )之间的关系如图所示.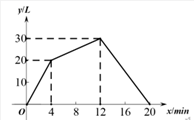
请根据相关信息,解答下列问题:
(1)、填表:时间/min
2
3
4
12
容器内水量/L
10
20
(2)、填空:①每分钟进水升,每分钟出水升;
②容器中储水量不低于15升的时长是分钟;
(3)、当 时,请直接写出 关于 的函数解析式.24. 将等边三角形 如图放置在平面直角坐标系中, , 为线段 的中点,将线段 绕点 逆时针旋转60°得线段 ,连接 .
(Ⅰ)如图1,求点 的坐标;
(Ⅱ)在图1中, 与 交于点 ,连接 , 为 的中点,连接 ,求线段 的长.请你补全图形,并完成计算;
(Ⅲ)如图2,将 绕点 逆时针旋转, 为线段 的中点, 为线段 的中点,连接 ,请直接写出在旋转过程中 的取值范围.
25. 如图,在平面直角坐标系中, 为原点,抛物线 ( , 为常数),经过点 和点 .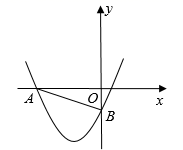 (1)、求抛物线的解析式;(2)、在抛物线上是否存在一点 ,使 ?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 为直线 下方抛物线上一点,点 为 轴上一点,当 的面积最大时,直接写出 的最小值.
(1)、求抛物线的解析式;(2)、在抛物线上是否存在一点 ,使 ?若存在,请求出点 的坐标,若不存在,请说明理由;(3)、点 为直线 下方抛物线上一点,点 为 轴上一点,当 的面积最大时,直接写出 的最小值.