山西省阳泉市盂县2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 2021的相反数是( )A、 -2021 B、 C、2021 D、2. 下面四个化学仪器示意图中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图,直线AB∥CD,∠3=70°,则∠1=( )
3. 如图,直线AB∥CD,∠3=70°,则∠1=( )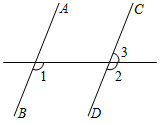 A、70° B、100° C、110° D、120°4. 对于无理数 ,添加关联的数或者运算符号组成新的式子,其运算结果能成为有理数的是( ).A、 B、 C、 D、5. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )
A、70° B、100° C、110° D、120°4. 对于无理数 ,添加关联的数或者运算符号组成新的式子,其运算结果能成为有理数的是( ).A、 B、 C、 D、5. 如图,△ABC与△DEF位似,点O为位似中心.已知OA∶OD=1∶2,则△ABC与△DEF的面积比为( )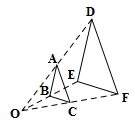 A、1∶2 B、1∶3 C、1∶4 D、1∶56. 计算: ( )A、 B、 C、 D、7. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、
A、1∶2 B、1∶3 C、1∶4 D、1∶56. 计算: ( )A、 B、 C、 D、7. 2020年初以来,红星消毒液公司生产的消毒液在库存量为m吨的情况下,日销售量与产量持平,自1月底抗击“新冠病毒”以来,消毒液需求量猛增,该厂在生产能力不变的情况下,消毒液一度脱销.下面表示2020年初至脱销期间,该厂库存量y(吨)与时间(天)之间函数关系的大致图象是( )A、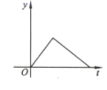 B、
B、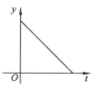 C、
C、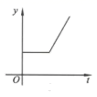 D、
D、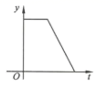 8. 下列说法错误的是( )A、定义反映出事物的本质属性.既可以做性质,也可以做判定 B、证明两个等边三角形全等,具需证明一边相等即可 C、有一个角是 的等腰三角形是等腰直角三角形 D、在放大镜下,一个字可以变大,一条线段可以变长,但是一个角的大小是不变的9. 将关于 的一元二次方程 变形为 ,就可以将 表示为关于 的一次多项式,从而达到“降次”的目的,又如 …,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且 ,则 的值为( )A、 B、 C、 D、10. 观察下列图形,它们是一组有规律的图案,各图形是由大小相同的黑点组成.图1中有2个点,图2中有 个点,图3中有14个点,…,按此规律,第10个图中黑点的个数是( )
8. 下列说法错误的是( )A、定义反映出事物的本质属性.既可以做性质,也可以做判定 B、证明两个等边三角形全等,具需证明一边相等即可 C、有一个角是 的等腰三角形是等腰直角三角形 D、在放大镜下,一个字可以变大,一条线段可以变长,但是一个角的大小是不变的9. 将关于 的一元二次方程 变形为 ,就可以将 表示为关于 的一次多项式,从而达到“降次”的目的,又如 …,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知: ,且 ,则 的值为( )A、 B、 C、 D、10. 观察下列图形,它们是一组有规律的图案,各图形是由大小相同的黑点组成.图1中有2个点,图2中有 个点,图3中有14个点,…,按此规律,第10个图中黑点的个数是( )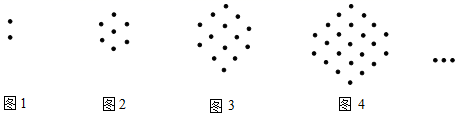 A、119 B、120 C、121 D、122
A、119 B、120 C、121 D、122二、填空题
-
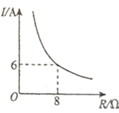
11. 2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于 秒,则 用科学记数法表示为 .12. 已知蓄电池的电压为定值,使用蓄电池时,电流 (单位: )与电阻 (单位: )成反比例函数关系,图像如图所示,则这个反比例函数解析式为 .
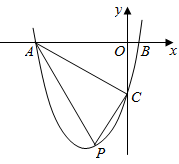
 13. 定义:如图,点 、点 把线段 分割成 和 ,若以 为边的三角形是一个直角三角形,则称点 、点 是线段 的勾股分割点.已知点 点 是线段 的勾股分割点, ,则 .
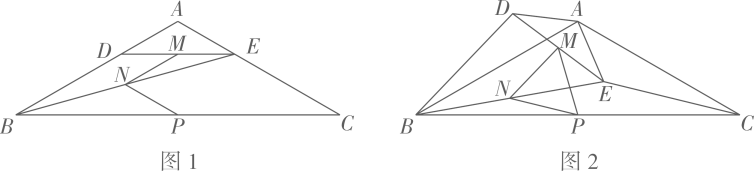
13. 定义:如图,点 、点 把线段 分割成 和 ,若以 为边的三角形是一个直角三角形,则称点 、点 是线段 的勾股分割点.已知点 点 是线段 的勾股分割点, ,则 . 14. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.
14. 《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1、2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺=10寸),则AB的长是寸.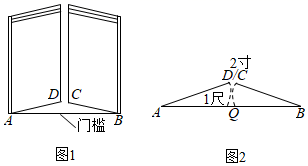
三、解答题
-
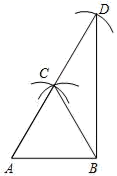
15. 如图,木工师傅在板材边角处做直角时,往往使用“三弧法”,其做法是:
⑴作线段AB , 分别以为A、B为圆心,AB长为半径作弧,两弧的交点为C;
⑵以C为圆心,仍以AB长为半径做弧,交AC的延长线于点D;
⑶连接BD、BC .
下列说法正确的是:(把所有正确的序号都写出来)
①∠CBD=30°; ②S△BDC= AB2;③点C是 的外心;④sin2A+cos2D=1
 16.(1)、计算:(2)、先化简,再求值: ,其中 .17. 如图, .求证: .
16.(1)、计算:(2)、先化简,再求值: ,其中 .17. 如图, .求证: .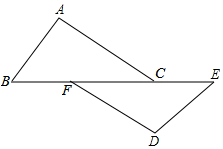 18. 为了解疫情期间学生网络学习的学习效果,盂县某中学随机抽取了部分学生进行调查,要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果,现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题:
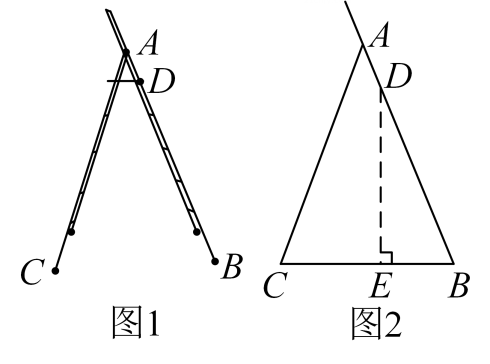
18. 为了解疫情期间学生网络学习的学习效果,盂县某中学随机抽取了部分学生进行调查,要求每位学生从“优秀”,“良好”,“一般”,“不合格”四个等次中,选择一项作为自我评价网络学习的效果,现将调查结果绘制成如图两幅不完整的统计图,请结合图中所给的信息解答下列问题: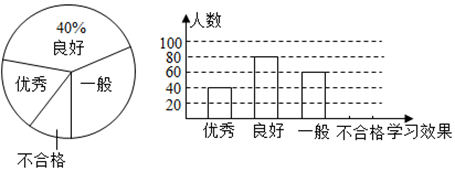 (1)、这次活动共抽查了人.(2)、将条形统计图补充完整,并计算出扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数;(3)、张老师在班上随机抽取了4名学生,其中学习效果“优秀”的1人,“良好”的2人,“一般”的1人,若再从这4人中随机抽取2人,请用画树状图法,求出抽取的2人学习效果是“一个优秀,一个良好”的概率.19. 人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点. 图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.
(1)、这次活动共抽查了人.(2)、将条形统计图补充完整,并计算出扇形统计图中,学习效果“一般”的学生人数所在扇形的圆心角度数;(3)、张老师在班上随机抽取了4名学生,其中学习效果“优秀”的1人,“良好”的2人,“一般”的1人,若再从这4人中随机抽取2人,请用画树状图法,求出抽取的2人学习效果是“一个优秀,一个良好”的概率.19. 人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点. 图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0. 1cm;参考数据sin70°≈0. 94,cos70°≈0. 34,sin20°≈0. 34,cos20°≈0. 94)
 20. 期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的90%?至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.21. 先阅读下面材科,再完成任务:
20. 期中考试后,某班班主任对在期中考试中取得优异成绩的同学进行表彰.她到商场购买了甲、乙两种笔记本作为奖品,购买甲种笔记本15个,乙种笔记本20个,共花费250元.已知购买一个甲种笔记本比购买一个乙种笔记本多花费5元.(1)、求购买一个甲种、一个乙种笔记本各需多少元?(2)、两种笔记本均受到了获奖同学的喜爱,班主任决定在期末考试后再次购买两种笔记本共35个,正好赶上商场对商品价格进行调整,甲种笔记本售价比上一次购买时减价2元,乙种笔记本按上一次购买时售价的8折出售.如果班主任此次购买甲、乙两种笔记本的总费用不超过上一次总费用的90%?至多需要购买多少个甲种笔记本?并求购买两种笔记本总费用的最大值.21. 先阅读下面材科,再完成任务:材料一:我们可以将任意三位数记为 ,(其中 分别表示该数的百位数字,十位数字和个位数字,且 ).显然 .
材料二:若一个三位数的百位数字,十位数字和个位数字均不为 ,则称之为原始数,比如 就是一个原始数,将原始数的三个数位上的数字交换顺序,可产生出 个新的原始数,比如由 可以产生出 这 个新原始数,将这 个数相加,得到的和1332称为由原始数 生成的终止数.
任务:
(1)、分别求出由下列两个原始数生成的终止数: ;(2)、若由一个原始数生成的终止数为1110求满足条件的所有原始数.