内蒙古包头市昆都仑区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、2. 人民日报讯,2020年6月23日,中国成功发射北斗系统第55颗导航卫星,至此中国提前半年全面完成北斗三号全球卫星导航系统星座部署.北斗三号卫星上配置的新一代国产原子钟,使北斗导航系统授时精度达到了十亿分之一秒.十亿分之一用科学记数法可以表示为( )A、 B、 C、 D、3. 实数a、b在数轴上的对应点的位置如图所示,下列式子成立的是( )
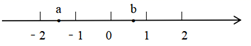 A、a>b B、|a|<|b| C、a+b<0 D、 >04. 下列运算正确的是( )A、 B、 C、 D、5. 如图,CD∥AB,点O在AB上,OE平分 BOD,OF⊥OE, D= ,则 AOF的度数是( )
A、a>b B、|a|<|b| C、a+b<0 D、 >04. 下列运算正确的是( )A、 B、 C、 D、5. 如图,CD∥AB,点O在AB上,OE平分 BOD,OF⊥OE, D= ,则 AOF的度数是( )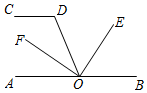 A、 B、 C、 D、6. 下图是由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
A、 B、 C、 D、6. 下图是由5个完全相同的小正方体组成的立体图形,它的俯视图是( ) A、
A、 B、
B、 C、
C、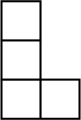 D、
D、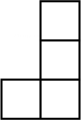 7. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差,从这四人中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )
7. 下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数与方差,从这四人中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )运动员
甲
乙
丙
丁
平均数( )
376
350
376
350
方差
12.5
13.5
2.4
5.4
A、甲 B、乙 C、丙 D、丁8. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=12,点D在边BC上,点E在线段AD上,EF⊥AC于点F,EG⊥EF交AB于点G,若EF=EG,则CD的长为( )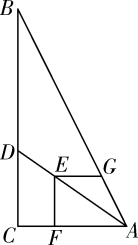 A、3.6 B、4 C、4.8 D、59. 如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是 上一点,则∠EPF的度数是( )
A、3.6 B、4 C、4.8 D、59. 如图,⊙O是等边△ABC的内切圆,分别切AB,BC,AC于点E,F,D,P是 上一点,则∠EPF的度数是( )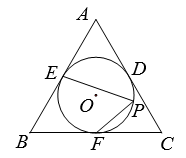 A、65° B、60° C、58° D、50°10. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2﹣10x+24=0的一个根,则该菱形ABCD的周长为( )A、16 B、24 C、16或24 D、4811. 如图,在平面直角坐标系中,矩形ABCD的顶点A , C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数 (k>0,x>0)的图象经过点B , 则k的值为( )
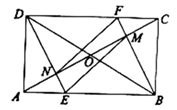
A、65° B、60° C、58° D、50°10. 若菱形ABCD的一条对角线长为8,边CD的长是方程x2﹣10x+24=0的一个根,则该菱形ABCD的周长为( )A、16 B、24 C、16或24 D、4811. 如图,在平面直角坐标系中,矩形ABCD的顶点A , C分别在x轴,y轴的正半轴上,点D(-2,3),AD=5,若反比例函数 (k>0,x>0)的图象经过点B , 则k的值为( )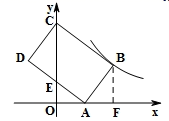 A、 B、8 C、10 D、12. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:
A、 B、8 C、10 D、12. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:① ;② ;③ ;④当 时,四边形 是菱形.其中,正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
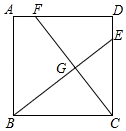
13. 函数 自变量x的取值范围是 .14. 已知关于x的分式方程 的解为非负数,则正整数m的所有个数为个.15. 计算: 的结果是 .16. 如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为 .
 17. 婷婷和她妈妈玩猜拳游戏.规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时婷婷获胜.那么,婷婷获胜的概率为.
17. 婷婷和她妈妈玩猜拳游戏.规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时婷婷获胜.那么,婷婷获胜的概率为. 18. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
18. 如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 . 19. 将二次函数 的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数 的图象有公共点,则实数b的取值范围是 .20. 如图,在平面直角坐标系中,点A的坐标是 ,点B在第一象限内, ,点E是线段 上的一个动点,连接 ,将射线 绕点E顺时针旋转 交 于点F , 当 最短时点F的坐标是 .
19. 将二次函数 的图象先向下平移1个单位,再向右平移3个单位,得到的图象与一次函数 的图象有公共点,则实数b的取值范围是 .20. 如图,在平面直角坐标系中,点A的坐标是 ,点B在第一象限内, ,点E是线段 上的一个动点,连接 ,将射线 绕点E顺时针旋转 交 于点F , 当 最短时点F的坐标是 .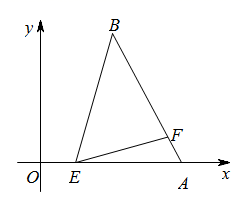
三、解答题
-
21. 一只不透明袋子中装有1个白球和若干个红球,这些球除颜色外都相同,某课外学习小组做摸球试验:将球搅匀后从中任意摸出1个球,记下颜色后放回、搅匀,不断重复这个过程,获得数据如下:
摸球的次数
200
300
400
1000
1600
2000
摸到白球的频数
72
93
130
334
532
667
摸到白球的频率
0.3600
0.3100
0.3250
0.3340
0.3325
0.3335
(1)、该学习小组发现,随着摸球次数的增多,摸到白球的频率在一个常数附近摆动,请直接写出这个常数(精确到0.01),由此估出红球有几个?(2)、在这次摸球试验中,从袋中随机摸出1个球,记下颜色后放回,再从中随机摸出1个球,利用画树状图或列表的方法表示所有可能出现的结果,并求两次摸到的球恰好1是个白球,1个是红球的概率.22. 如图,一艘渔船位于小岛 的北偏东 方向,距离小岛 的点 处,它沿着点 的南偏东 的方向航行. (1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?23. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.
(1)、渔船航行多远距离小岛 最近(结果保留根号)?(2)、渔船到达距离小岛 最近点后,按原航向继续航行 到点 处时突然发生事故,渔船马上向小岛 上的救援队求救,问救援队从 处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少(结果保留根号)?23. 某企业接到生产一批设备的订单,要求不超过12天完成.这种设备的出厂价为1200元/台,该企业第一天生产22台设备,第二天开始,每天比前一天多生产2台.若干天后,每台设备的生产成本将会增加,设第x天(x为整数)的生产成本为m(元台),m与x的关系如图所示.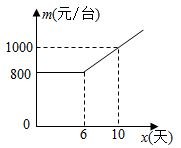 (1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.24. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
(1)、若第x天可以生产这种设备y台,则y与x的函数关系式为 , x的取值范围为;(2)、第几天时,该企业当天的销售利润最大?最大利润为多少?(3)、求当天销售利润低于10800元的天数.24. 已知,如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.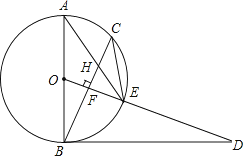 (1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
(1)、求证:BD是⊙O的切线;(2)、求证:CE2=EH•EA;(3)、若⊙O的半径为5,sinA= , 求BH的长。
25. 如图,在平面直角坐标系xOy中,矩形ABCD的边AB=4,BC=6.若不改变矩形ABCD的形状和大小,当矩形顶点A在x轴的正半轴上左右移动时,矩形的另一个顶点D始终在y轴的正半轴上随之上下移动.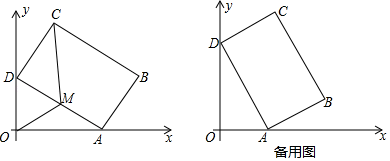 (1)、当∠OAD=30°时,求点C的坐标;(2)、设AD的中点为M,连接OM、MC,当四边形OMCD的面积为 时,求OA的长;(3)、当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.26. 如图,抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C . 直线l与抛物线交于A , D两点,与y轴交于点E , 点D的坐标为 .
(1)、当∠OAD=30°时,求点C的坐标;(2)、设AD的中点为M,连接OM、MC,当四边形OMCD的面积为 时,求OA的长;(3)、当点A移动到某一位置时,点C到点O的距离有最大值,请直接写出最大值,并求此时cos∠OAD的值.26. 如图,抛物线 与x轴交于A , B两点(点A在点B的左侧),与y轴交于点C . 直线l与抛物线交于A , D两点,与y轴交于点E , 点D的坐标为 .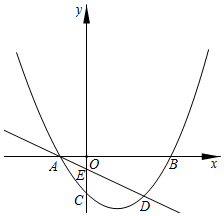 (1)、求A , B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 ,过点P作 轴,垂足为M . 与直线l交于点N , 当点N是线段 的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 ,求点Q的坐标.
(1)、求A , B两点的坐标及直线l的函数表达式;(2)、若点P是抛物线上的点,点P的横坐标为 ,过点P作 轴,垂足为M . 与直线l交于点N , 当点N是线段 的三等分点时,求点P的坐标;(3)、若点Q是y轴上的点,且 ,求点Q的坐标.