内蒙古包头市东河区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 若 则a+b的值是( )A、2 B、1 C、0 D、-12. 在网上搜索引擎中输入“2016中考”,能搜索到与之相关的结果个数约为0.564亿,这个数用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、a3•a3=a9 B、(﹣3a3)2=9a6 C、5a+3b=8ab D、(a+b)2=a2+b24. 如图, 中, ,点D在 上, .若 ,则 的长度为( )
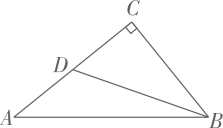 A、 B、 C、 D、45. 某几何体的三视图如图所示,则下列说法错误的是( )
A、 B、 C、 D、45. 某几何体的三视图如图所示,则下列说法错误的是( )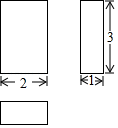 A、该几何体是长方体 B、该几何体的高是3 C、底面有一边的长是1 D、该几何体的表面积为18平方单位6. 下列说法正确的是( )A、为了解三名学生的视力情况,采用抽样调查 B、任意画一个三角形,其内角和是 是必然事件 C、甲、乙两名射击运动员10次射击成绩(单位:环)的平均数分别为 、 ,方差分别为 、 .若 , , ,则甲的成绩比乙的稳定 D、一个抽奖活动中,中奖概率为 ,表示抽奖20次就有1次中奖7. 如图,在菱形 中,点E是 的中点,以C为圆心、 为半径作弧,交 于点F , 连接 、 ,若 ,则阴影部分的面积为( )
A、该几何体是长方体 B、该几何体的高是3 C、底面有一边的长是1 D、该几何体的表面积为18平方单位6. 下列说法正确的是( )A、为了解三名学生的视力情况,采用抽样调查 B、任意画一个三角形,其内角和是 是必然事件 C、甲、乙两名射击运动员10次射击成绩(单位:环)的平均数分别为 、 ,方差分别为 、 .若 , , ,则甲的成绩比乙的稳定 D、一个抽奖活动中,中奖概率为 ,表示抽奖20次就有1次中奖7. 如图,在菱形 中,点E是 的中点,以C为圆心、 为半径作弧,交 于点F , 连接 、 ,若 ,则阴影部分的面积为( )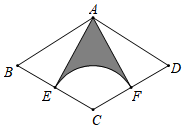 A、 B、 C、 D、8. 若满足方程组 的x与y互为相反数,则m的值为( )A、2 B、-2 C、11 D、-119. 如图, 的内接正五边形 的对角线 与 相交于点G , ,则 的长是( )
A、 B、 C、 D、8. 若满足方程组 的x与y互为相反数,则m的值为( )A、2 B、-2 C、11 D、-119. 如图, 的内接正五边形 的对角线 与 相交于点G , ,则 的长是( ) A、 B、 C、 D、10. 已知下列命题:①若 ,则 ;②若 ,则 ;③内错角相等;④周长相等的所有等腰直角三角形全等,其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② ;③ac-b+1=0;④OA·OB= .其中正确结论的个数是( )
A、 B、 C、 D、10. 已知下列命题:①若 ,则 ;②若 ,则 ;③内错角相等;④周长相等的所有等腰直角三角形全等,其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个11. 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC.则下列结论:①abc<0;② ;③ac-b+1=0;④OA·OB= .其中正确结论的个数是( )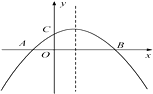 A、4 B、3 C、2 D、112. 如图,在矩形 中, ,点E是边 上一动点,将 沿直线 对折,点A的落点为 ,当 为直角三角形时,线段 的长为( )
A、4 B、3 C、2 D、112. 如图,在矩形 中, ,点E是边 上一动点,将 沿直线 对折,点A的落点为 ,当 为直角三角形时,线段 的长为( ) A、3 B、4 C、6或3 D、3或4
A、3 B、4 C、6或3 D、3或4二、填空题
-
13. 计算: .14. 如图,在 中,四边形 是圆内接四边形, ,则 的度数是 .
 15. 关于x的分式方程 的解为正数,则m的取值范围是.16. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为 .
15. 关于x的分式方程 的解为正数,则m的取值范围是.16. 如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为 . 17. 如图,点A的坐标为(﹣4,0),直线y= x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为 .
17. 如图,点A的坐标为(﹣4,0),直线y= x+n与坐标轴交于点B、C,连接AC,如果∠ACD=90°,则n的值为 . 18. 如图,过原点的直线与反比例函数y= (x>0)、反比例函数y= (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y= (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为 .
18. 如图,过原点的直线与反比例函数y= (x>0)、反比例函数y= (x>0)的图象分别交于A、B两点,过点A作y轴的平行线交反比例函数y= (x>0)的图象于C点,以AC为边在直线AC的右侧作正方形ACDE,点B恰好在边DE上,则正方形ACDE的面积为 .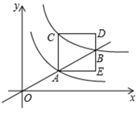 19. 如图,在 中, ,以AB为直径的 分别交AC , BC于点D , E , 过点B作 的切线与AC的延长线交于点F , 若 , ,则BF的长为 .
19. 如图,在 中, ,以AB为直径的 分别交AC , BC于点D , E , 过点B作 的切线与AC的延长线交于点F , 若 , ,则BF的长为 .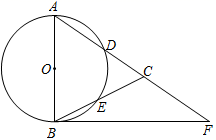 20. 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:(1)BF为∠ABE的角平分线;(2)DF=2BF;(3)2AB2=DF•DB;(4)sin∠BAE= .其中正确的结论为(填序号)
20. 菱形ABCD中,AE⊥BC于E,交BD于F点,下列结论:(1)BF为∠ABE的角平分线;(2)DF=2BF;(3)2AB2=DF•DB;(4)sin∠BAE= .其中正确的结论为(填序号)
三、解答题
-
21. 某中学对全校九年级学生进行了一次数学模拟考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给信息,解答下列问题:
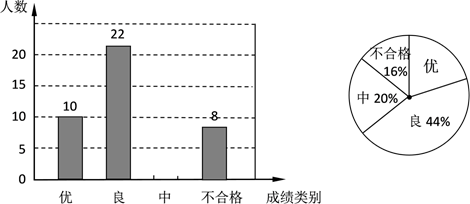 (1)、将条形统计图补充完整;(2)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是度;(3)、学校九年级共有600人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩类别可以达到“中”(不包括“中”)以上?(4)、学校准备从成绩进步最大的3名同学(1名男生、2名女生)中随机选取2名同学介绍学习经验,则选出的同学恰好是2名女生的概率是 .22. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )
(1)、将条形统计图补充完整;(2)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角是度;(3)、学校九年级共有600人参加了这次数学考试,估算该校九年级共有多少名学生的数学成绩类别可以达到“中”(不包括“中”)以上?(4)、学校准备从成绩进步最大的3名同学(1名男生、2名女生)中随机选取2名同学介绍学习经验,则选出的同学恰好是2名女生的概率是 .22. 疫情期间,为了保障大家的健康,各地采取了多种方式进行预防,某地利用无人机规劝居民回家.如图,一条笔直的街道 ,在街道 处的正上方 处有一架无人机,该无人机在 处测得俯角为 的街道 处有人聚集,然后沿平行于街道 的方向再向前飞行60米到达 处,在 处测得俯角为 的街道 处也有人聚集,已知两处聚集点 之间的距离为120米,求无人机飞行的高度 .(参考数据: , , , )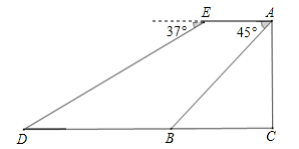 23. 在国家“一带一路”的倡议下,2018年6月将在浙江宁波举办中国 中东欧国家投资贸易博览会,某东欧客商准备在宁波采购一批特色商品.
23. 在国家“一带一路”的倡议下,2018年6月将在浙江宁波举办中国 中东欧国家投资贸易博览会,某东欧客商准备在宁波采购一批特色商品. (1)、根据以上信息,求一件A,B型商品的进价分别为多少元?(2)、若该东欧客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元 件,B型商品的售价为220元 件,且全部售出,设购进A型商品m件,写出该客商销售这批商品的利润与m之间的函数关系式,并求出利润的最大值.24. 如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点D , E , F , 且 . 是 的外接圆, 的平分线交 于点G , 交 于点H , 连接 、 .
(1)、根据以上信息,求一件A,B型商品的进价分别为多少元?(2)、若该东欧客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元 件,B型商品的售价为220元 件,且全部售出,设购进A型商品m件,写出该客商销售这批商品的利润与m之间的函数关系式,并求出利润的最大值.24. 如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点D , E , F , 且 . 是 的外接圆, 的平分线交 于点G , 交 于点H , 连接 、 . (1)、求证: ;(2)、试判断 与 的位置关系,并说明理由;(3)、若 ,求 的值.25. 某校数学活动小组在一次活动中,对一个数学问题作如下探究:
(1)、求证: ;(2)、试判断 与 的位置关系,并说明理由;(3)、若 ,求 的值.25. 某校数学活动小组在一次活动中,对一个数学问题作如下探究: (1)、问题发现:如图1,在等边 中,点P是边 上任意一点(不含端点B和C),连接 ,以 为边作等边 ,连接 .求证: ;(2)、变式探究:如图2,在等腰 中, ,点P是边 上任意一点(不含端点B和C),连接 以 为腰作等腰 ,使 ,连接 .判断 和 的数量关系,并说明理由;(3)、解决问题:如图3,在正方形 中,点P是边 上一点,以 为边作正方形 ,Q是正方形 的中心,连接 .若正方形 的边长为8, ,求正方形 的边长.26. 如图,已知抛物线 经过 , 两点,与x轴负半轴交于点C , 连接 、 .
(1)、问题发现:如图1,在等边 中,点P是边 上任意一点(不含端点B和C),连接 ,以 为边作等边 ,连接 .求证: ;(2)、变式探究:如图2,在等腰 中, ,点P是边 上任意一点(不含端点B和C),连接 以 为腰作等腰 ,使 ,连接 .判断 和 的数量关系,并说明理由;(3)、解决问题:如图3,在正方形 中,点P是边 上一点,以 为边作正方形 ,Q是正方形 的中心,连接 .若正方形 的边长为8, ,求正方形 的边长.26. 如图,已知抛物线 经过 , 两点,与x轴负半轴交于点C , 连接 、 . (1)、求该抛物线的解析式;(2)、D、E分别为 、 的中点,连接 ,P为 上的动点, ,垂足为Q , ,垂足为N , 连接 .
(1)、求该抛物线的解析式;(2)、D、E分别为 、 的中点,连接 ,P为 上的动点, ,垂足为Q , ,垂足为N , 连接 .①当 与 相似时,求点P的坐标;
②是否存在点P , 使得 ,若存在,直接写出点P的坐标,若不存在,请说明理由.