辽宁省锦州市黑山县2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期,2021的相反数是( )A、2021 B、-2021 C、- D、2. 下面的几何图形是由四个相同的小正方体搭成的,其中主视图和左视图相同的是( )A、
 B、
B、 C、
C、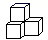 D、
D、 3. 下列调查工作需采用普查方式的是( )A、锦州市环保局对大凌河某段水域的水污染情况的调查 B、锦州市电视台对正在播出的某电视节目收视率的调查 C、锦州市质检部门对各厂家生产的电池使用寿命的调查 D、神舟十号飞船发射前,工作人员对其各个零部件安全情况的检查4. 为了调查某小区居民的口罩使用情况,随机抽查了 10 户家庭的一周使用的口罩数,结果如表,则关于这 10 户家庭的一周使用的口罩数,下列说法错误的是( )
3. 下列调查工作需采用普查方式的是( )A、锦州市环保局对大凌河某段水域的水污染情况的调查 B、锦州市电视台对正在播出的某电视节目收视率的调查 C、锦州市质检部门对各厂家生产的电池使用寿命的调查 D、神舟十号飞船发射前,工作人员对其各个零部件安全情况的检查4. 为了调查某小区居民的口罩使用情况,随机抽查了 10 户家庭的一周使用的口罩数,结果如表,则关于这 10 户家庭的一周使用的口罩数,下列说法错误的是( )每周用的口罩数量
20
21
23
30
总数
3
4
2
1
A、方差是 5 B、众数是 21 C、极差是 10 D、中位数是 215. 下列二次根式中属于最简二次根式的是( )A、 B、 C、 D、6. 若关于x的一元二次方程(m﹣1)x2+x+1=0有两个实数根,则m的取值范围是( )A、m≤ B、m> C、m≤ 且m≠1 D、m< 且m≠17. 如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则①二次函数的最大值为a+b+c;②a﹣b+c<0;③b2﹣4ac<0;④当y>0时,﹣1<x<3,其中结论正确的有( )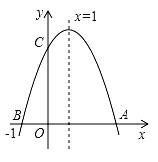 A、①③ B、①④ C、①② D、①③④8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
A、①③ B、①④ C、①② D、①③④8. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )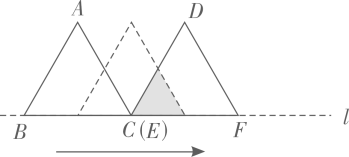 A、
A、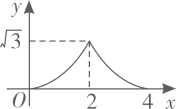 B、
B、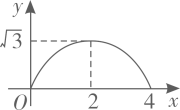 C、
C、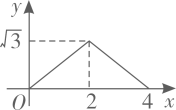 D、
D、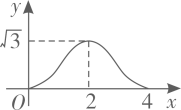
二、填空题
-
9. 分解因式:m2n﹣2mn+n= .10. 从辽宁省工商联获悉,自新型冠状病毒引发的肺炎疫情出现以来,截止2月13日下午6点,全省民营企业、商会及企业家个人累计7412家(人),共向武汉等疫情严重地区及我省定点防治新冠肺炎的医院、政府部门、执勤卡点等捐赠物款约10.1亿元.10.1亿用科学记数法表示应为.11.
如图,已知l1∥l2 , ∠A=40°,∠1=60°,∠2= .
 12. 如图,有下面几张扑克牌,把牌背面朝上,随机抽取一张,则恰好抽到黑桃J 的概率是 .
12. 如图,有下面几张扑克牌,把牌背面朝上,随机抽取一张,则恰好抽到黑桃J 的概率是 . 13. 如图,小杨将一个三角板放在⊙O上,使三角板的一直角边经过圆心O , 测得AC=5cm , AB=3cm , 则⊙O的半径长为 .
13. 如图,小杨将一个三角板放在⊙O上,使三角板的一直角边经过圆心O , 测得AC=5cm , AB=3cm , 则⊙O的半径长为 . 14. 如图,在 中, ,点A在反比例函数 ( , )的图象上,点B,C在x轴上, ,延长 交y轴于点D,连接 ,若 的面积等于1,则k的值为.
14. 如图,在 中, ,点A在反比例函数 ( , )的图象上,点B,C在x轴上, ,延长 交y轴于点D,连接 ,若 的面积等于1,则k的值为.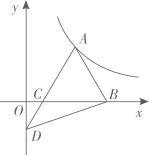 15. 菱形ABCD的对角线AC , BD相交于点O , E是AD的中点,点F , G在AB上,EF⊥AB , OG∥EF . AD=10,EF=4,则BG的长 .
15. 菱形ABCD的对角线AC , BD相交于点O , E是AD的中点,点F , G在AB上,EF⊥AB , OG∥EF . AD=10,EF=4,则BG的长 . 16. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y= x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长及S3的值分别为 .
16. 如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y= x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(27,9),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长及S3的值分别为 .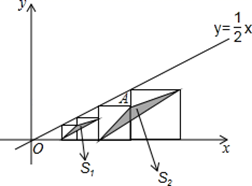
三、解答题
-
17. 先化简,再求值: ,其中 .18. 由于疫情的影响,学生不能返校上课,某校在直播授课的同时还为学生提供了四种辅助学习方式:A网上自测,B网上阅读,C网上答疑,D网上讨论.为了解学生对四种学习方式的喜欢情况,该校随机抽取部分学生进行问卷调查,规定被调查学生从四种方式中选择自己最喜欢的一种,根据调查结果绘制成如下两幅不完整的统计图:

根据统计图提供的信息,解答下列问题:
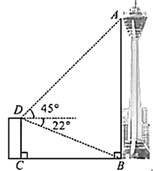
(1)、本次共调查了名学生;(2)、在扇形统计图中,m的值是 , D对应的扇形圆心角的度数是;(3)、请补全条形统计图;(4)、若该校共有2000名学生,根据抽样调查的结果,请你估计该校最喜欢方式D的学生人数.19. 共享经济已经进入人们的生活.小沈收集了自己感兴趣的4个共享经济领域的图标,共享出行、共享服务、共享物品、共享知识,制成编号为A、B、C、D的四张卡片(除字母和内容外,其余完全相同).现将这四张卡片背面朝上,洗匀放好. (1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 今年植树节期间,某景观园林公司购进一批成捆的A,B两种树苗,每捆 种树苗比每捆B种树苗多10棵,每捆A种树苗和每捆B种树苗的价格分别是630元和600元,而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.(1)、求这一批树苗平均每棵的价格是多少元?(2)、如果购进的这批树苗共5500棵,A种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进A种树苗和B种树苗各多少棵?并求出最低费用.21. 成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶 处测得塔 处的仰角为45°,塔底部 处的俯角为22°.已知建筑物的高 约为61米,请计算观景台的高 的值.
(1)、小沈从中随机抽取一张卡片是“共享服务”的概率是;(2)、小沈从中随机抽取一张卡片(不放回),再从余下的卡片中随机抽取一张,请你用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率.(这四张卡片分别用它们的编号A、B、C、D表示)20. 今年植树节期间,某景观园林公司购进一批成捆的A,B两种树苗,每捆 种树苗比每捆B种树苗多10棵,每捆A种树苗和每捆B种树苗的价格分别是630元和600元,而每棵A种树苗和每棵B种树苗的价格分别是这一批树苗平均每棵价格的0.9倍和1.2倍.(1)、求这一批树苗平均每棵的价格是多少元?(2)、如果购进的这批树苗共5500棵,A种树苗至多购进3500棵,为了使购进的这批树苗的费用最低,应购进A种树苗和B种树苗各多少棵?并求出最低费用.21. 成都“339”电视塔作为成都市地标性建筑之一,现已成为外地游客到成都旅游打卡的网红地.如图,为测量电视塔观景台 处的高度,某数学兴趣小组在电视塔附近一建筑物楼顶 处测得塔 处的仰角为45°,塔底部 处的俯角为22°.已知建筑物的高 约为61米,请计算观景台的高 的值.(结果精确到1米;参考数据: , , )
 22. 如图,AB为⊙O的直径,C为BA延长线上一点,点D为圆上一点且∠ADC=∠AOF , OF⊥AD于点E , 交CD于点F .
22. 如图,AB为⊙O的直径,C为BA延长线上一点,点D为圆上一点且∠ADC=∠AOF , OF⊥AD于点E , 交CD于点F . (1)、判断CD与⊙O的位置关系;(2)、若sinC= ,BD=8,求EF的长.23. 开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
(1)、判断CD与⊙O的位置关系;(2)、若sinC= ,BD=8,求EF的长.23. 开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示. (1)、图中线段AB所表示的实际意义是;(2)、请直接写出y与x之间的函数关系式;(3)、已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?24. 如图1,在等边三角形ABC的外角∠CAH内引射线AM , 作点C关于AM的对称点E(点E在∠CAH内),连接BE , BE、CE分别交AM于点F、G .
(1)、图中线段AB所表示的实际意义是;(2)、请直接写出y与x之间的函数关系式;(3)、已知该文具批发部这种笔记本的进价是3元/本,若小明购买此种笔记本超过10本但不超过20本,那么小明购买多少本时,该文具批发部在这次买卖中所获的利润W(元)最大?最大利润是多少?24. 如图1,在等边三角形ABC的外角∠CAH内引射线AM , 作点C关于AM的对称点E(点E在∠CAH内),连接BE , BE、CE分别交AM于点F、G .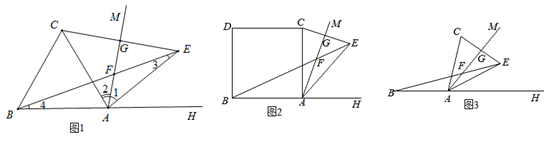 (1)、完成下列问题:①∠FEG= ▲ ;
(1)、完成下列问题:①∠FEG= ▲ ;②求证:BF=AF+2FG .
(2)、把(1)中的“等边三角形ABC”改为“正方形ABCD”,其余条件不变,如图2.完成下列问题:
①∠FEG= ▲ ;
②线段BF、AF、FG之间存在怎样的数量关系?说明理由.
(3)、如图3,点A在射线BH上,AB=AC , ∠BAC=α ,在∠CAH内引射线AM , 作点C关于AM的对称点E(点E在∠CAH内),连接BE , BE、CE分别交AM于点F、G . 直接写出线段BF、AF、GF之间的数量关系.25. 已知抛物线 与x轴交于点 ,点 ,与y轴交于点 ,顶点为点D.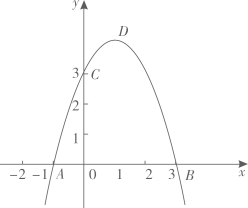 (1)、求抛物线的解析式;(2)、若过点C的直线交线段AB于点E,且 ,求直线CE的解析式(3)、若点P在抛物线上,点Q在x轴上,当以点D、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;(4)、已知点 ,在抛物线对称轴上找一点F,使 的值最小此时,在抛物线上是否存在一点K,使 的值最小,若存在,求出点K的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若过点C的直线交线段AB于点E,且 ,求直线CE的解析式(3)、若点P在抛物线上,点Q在x轴上,当以点D、C、P、Q为顶点的四边形是平行四边形时,求点P的坐标;(4)、已知点 ,在抛物线对称轴上找一点F,使 的值最小此时,在抛物线上是否存在一点K,使 的值最小,若存在,求出点K的坐标;若不存在,请说明理由.