辽宁省鞍山市立山区2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 数1,0, ,﹣2中最大的是( )A、1 B、0 C、 D、﹣22. 如图,已知a∥b , 小华把三角板的直角顶点放在直线a上.若∠1=40°,则∠2的度数为( )
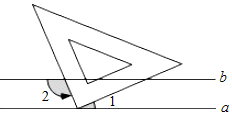 A、100° B、110° C、120° D、130°3. 下列各式运算正确的是( )A、2(a﹣1)=2a﹣1 B、a2b﹣ab2=0 C、a2+a2=2a2 D、2a3﹣3a3=a34. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A、100° B、110° C、120° D、130°3. 下列各式运算正确的是( )A、2(a﹣1)=2a﹣1 B、a2b﹣ab2=0 C、a2+a2=2a2 D、2a3﹣3a3=a34. 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )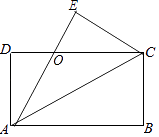 A、6cm B、7cm C、8cm D、9cm5. 在创建“全国文明城市”期间,济南市某中学组织共青团员植树,其中七位同学植树的棵数分别为:3、1、1、3、2、3、2,则这组数据的中位数和众数分别是( )A、3,2 B、2,3 C、2,2 D、3,36. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°7. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA1B1C1的位置,若OA=2,∠C=120°,则点B1的坐标为( )
A、6cm B、7cm C、8cm D、9cm5. 在创建“全国文明城市”期间,济南市某中学组织共青团员植树,其中七位同学植树的棵数分别为:3、1、1、3、2、3、2,则这组数据的中位数和众数分别是( )A、3,2 B、2,3 C、2,2 D、3,36. 若圆锥的侧面积等于其底面积的3倍,则该圆锥侧面展开图所对应扇形圆心角的度数为( )A、60° B、90° C、120° D、180°7. 如图,菱形OABC的一边OA在x轴上,将菱形OABC绕原点O逆时针旋转105°至OA1B1C1的位置,若OA=2,∠C=120°,则点B1的坐标为( ) A、(﹣3, ) B、(3, ) C、(﹣ , ) D、( ,﹣ )8. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )
A、(﹣3, ) B、(3, ) C、(﹣ , ) D、( ,﹣ )8. 如图,在△ABC中,∠C=90°,AC=BC=3cm.动点P从点A出发,以 cm/s的速度沿AB方向运动到点B.动点Q同时从点A出发,以1cm/s的速度沿折线AC CB方向运动到点B.设△APQ的面积为y(cm2).运动时间为x(s),则下列图象能反映y与x之间关系的是( )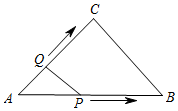 A、
A、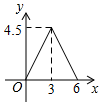 B、
B、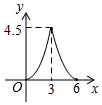 C、
C、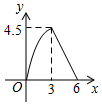 D、
D、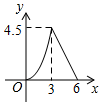
二、填空题
-
9. 函数y= 中,自变量x的取值范围是 .10. 如图,四边形ABCD是正方形,AE⊥BE于点E , 且AE=3,BE=4,则阴影部分的面积是 .
 11. 预计到2025年我国高铁运营里程将达到38 000公里.将数据38 000用科学记数法表示为 .12. 如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 .
11. 预计到2025年我国高铁运营里程将达到38 000公里.将数据38 000用科学记数法表示为 .12. 如图,在△ABC中,M,N分别是AB和AC的中点,连接MN,点E是CN的中点,连接ME并延长,交BC的延长线于点D.若BC=4,则CD的长为 . 13. 若关于x的一元二次方程 无实数根,则k的取值范围是.14. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .
13. 若关于x的一元二次方程 无实数根,则k的取值范围是.14. 如图,⊙O是等边△ABC的内切圆,分别切AB , BC , AC于点E , F , D , P是 上一点,则∠EPF的度数是 .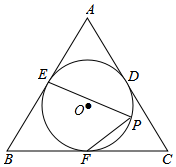 15. A、B两地相距 ,甲骑自行车从A地到B地,出发 后,乙骑摩托车从A地到B地,且乙比甲早到 ,已知甲、乙的速度之比为1:3,则甲的速度是 .16. 如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A , 作线段OD的垂直平分线BE交x轴于点E , 交AD于点B , 作射线OB , 以AB为边在△AOB的外侧作正方形ABCA1 , 延长A1C交射线OB于点B1 , 以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2 , 延长A2C1交射线OB于点B2 , 以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3…按此规律进行下去,则正方形A2020B2020C2020A2021的周长为 .
15. A、B两地相距 ,甲骑自行车从A地到B地,出发 后,乙骑摩托车从A地到B地,且乙比甲早到 ,已知甲、乙的速度之比为1:3,则甲的速度是 .16. 如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A , 作线段OD的垂直平分线BE交x轴于点E , 交AD于点B , 作射线OB , 以AB为边在△AOB的外侧作正方形ABCA1 , 延长A1C交射线OB于点B1 , 以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2 , 延长A2C1交射线OB于点B2 , 以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3…按此规律进行下去,则正方形A2020B2020C2020A2021的周长为 .
三、解答题
-
17. 先化简,再求值:( +x﹣1)÷ ,其中x=( )﹣1+(﹣3)0 .
18. 如图,▱ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由. 19. 在疫情期间,为落实停课不停学,某校对本校学生某一学科在家学习的情况进行抽样调查,了解到学生的学习方式有:电视直播、任教老师在线辅导、教育机构远程教学、自主学习,参入调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图,解答下列问题.
19. 在疫情期间,为落实停课不停学,某校对本校学生某一学科在家学习的情况进行抽样调查,了解到学生的学习方式有:电视直播、任教老师在线辅导、教育机构远程教学、自主学习,参入调查的学生只能选择一种学习方式,将调查结果绘制成不完整的扇形统计图和条形统计图,解答下列问题.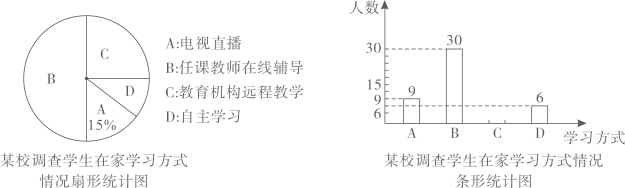 (1)、本次受调查的学生有人;(2)、补全条形统计图;(3)、根据调查结果,若本校有1800名学生,估计有多少名学生与任课教师在线辅导?20. 4件同型号的产品中,有1件不合格品和3件合格品.(1)、从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;(2)、从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;(3)、在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?21. 如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)、本次受调查的学生有人;(2)、补全条形统计图;(3)、根据调查结果,若本校有1800名学生,估计有多少名学生与任课教师在线辅导?20. 4件同型号的产品中,有1件不合格品和3件合格品.(1)、从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;(2)、从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;(3)、在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?21. 如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN). (1)、求灯杆CD的高度;
(1)、求灯杆CD的高度;
(2)、求AB的长度(结果精确到0.1米).(参考数据: =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
22. 如图,正比例函数 的图象与反比例函数 在第一象限的图象交于 点,过 点作 轴的垂线,垂足为 ,已知 的面积为1. (1)、求反比例函数的解析式;(2)、如果 为反比例函数在第一象限图象上的点(点 与点 不重合),且 点的横坐标为1,在 轴上求一点 ,使 最小.
(1)、求反比例函数的解析式;(2)、如果 为反比例函数在第一象限图象上的点(点 与点 不重合),且 点的横坐标为1,在 轴上求一点 ,使 最小.
23. 如图,△ABC内接于⊙O , AB是⊙O的直径,弦CD与AB交于点E , 连接AD , 过点A作直线MN , 使∠MAC=∠ADC .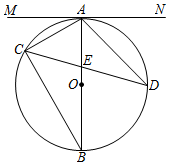 (1)、求证:直线MN是⊙O的切线.(2)、若∠ADC=30°,AB=8,AE=3,求DE的长.24. 某工厂生产A型产品,每件成本为20元,销售A型产品的销售单价x元时,销售量为y万件,要求每件A型产品的售价不低于20元且不高于30元,y与x之间满足一次函数关系:当销售单价为23元时,销售量为34万件;当销售单价为25元时,销售量为30万件.(1)、请直接写出y与x的函数关系式;(2)、某次销售刚好获得182万元的利润,每件A型产品的售价是多少元?(3)、设该工厂销售A型产品所获得的利润为w万元,将该产品销售单价定为多少元时,才能使销售该产品所获利润最大?最大利润是多少?25. 如图,在△ABC中,∠ACB=90°,AC=BC , 以C为顶点作等腰直角△CMN , 使∠CMN=90°,连接BN , 射线NM交BC于点D .
(1)、求证:直线MN是⊙O的切线.(2)、若∠ADC=30°,AB=8,AE=3,求DE的长.24. 某工厂生产A型产品,每件成本为20元,销售A型产品的销售单价x元时,销售量为y万件,要求每件A型产品的售价不低于20元且不高于30元,y与x之间满足一次函数关系:当销售单价为23元时,销售量为34万件;当销售单价为25元时,销售量为30万件.(1)、请直接写出y与x的函数关系式;(2)、某次销售刚好获得182万元的利润,每件A型产品的售价是多少元?(3)、设该工厂销售A型产品所获得的利润为w万元,将该产品销售单价定为多少元时,才能使销售该产品所获利润最大?最大利润是多少?25. 如图,在△ABC中,∠ACB=90°,AC=BC , 以C为顶点作等腰直角△CMN , 使∠CMN=90°,连接BN , 射线NM交BC于点D . (1)、如图1,若点A , M , N在一条直线上.
(1)、如图1,若点A , M , N在一条直线上.①求证:BN+CM=AM;
②若AM=6,BN=2,求BD的长;
(2)、如图2.若AB=4,CN=2,将△CMN绕点C逆时针旋转一周,在旋转过程中射线NM交AB于点H , 当三角形DBH是直角三角形时,请你直接写出CD的长.26. 已知二次函数 的图象与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C . (1)、求抛物线的解析式;(2)、若点P是抛物线上一动点,满足∠PAB=2∠ACO , 求P点的坐标;(3)、在(2)的条件下,当P点在x轴上方时,作PH⊥x轴于H , 点M是线段OH上一动点,MD⊥CM交PH于点D , 连接CD , 点Q为CD中点,求QM的最小值.
(1)、求抛物线的解析式;(2)、若点P是抛物线上一动点,满足∠PAB=2∠ACO , 求P点的坐标;(3)、在(2)的条件下,当P点在x轴上方时,作PH⊥x轴于H , 点M是线段OH上一动点,MD⊥CM交PH于点D , 连接CD , 点Q为CD中点,求QM的最小值.