黑龙江省齐齐哈尔市铁锋区2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 的倒数的相反数( )A、2021 B、 C、-2021 D、2. 下列计算正确的是( )A、2a+3a=6a B、a2+a3=a5 C、a8÷a2=a6 D、(a3)4=a73. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、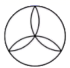 4. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )
4. 如图是由七个相同的小正方体堆成的物体,这个物体的俯视图是( )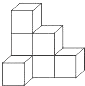 A、
A、 B、
B、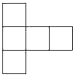 C、
C、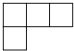 D、
D、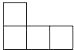 5. 为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
5. 为弘扬传统文化,某校初二年级举办传统文化进校园朗诵大赛,小明同学根据比赛中九位评委所给的某位参赛选手的分数,制作了一个表格,如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )中位数
众数
平均数
方差
9.2
9.3
9.1
0.3
A、中位数 B、众数 C、平均数 D、方差6. 矩形ABCD的边BC在直线l上,AB=2,BC=4,P是AD边上一动点且不与点D重合,连结CP,过点P作∠APE=∠CPD,交直线l于点E,若PD的长为x,△PEC与矩形ABCD重合部分的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 张老师到文具店购买A、B两种文具,A种文具每件2.5元,B种文具每件1元,共花了30元钱,则可供他选择的购买方案的个数为(两样都买)( )A、4 B、5 C、6 D、78. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为( )
7. 张老师到文具店购买A、B两种文具,A种文具每件2.5元,B种文具每件1元,共花了30元钱,则可供他选择的购买方案的个数为(两样都买)( )A、4 B、5 C、6 D、78. 如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y (x>0)的图象经过A,B两点,若菱形ABCD的面积为2 ,则k的值为( )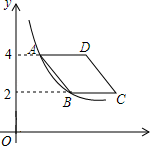 A、2 B、3 C、4 D、69. 如果关于 的分式方程 无解,那么 的值为( )A、4 B、-4 C、2 D、-210. 如图是抛物线 ,其顶点坐标为 ,且与x轴的一个交点在点 和 之间,下列结论:
A、2 B、3 C、4 D、69. 如果关于 的分式方程 无解,那么 的值为( )A、4 B、-4 C、2 D、-210. 如图是抛物线 ,其顶点坐标为 ,且与x轴的一个交点在点 和 之间,下列结论:① ;② ;③ ;④ ;⑤关于x的方程 的另一个解在-2和-3之间,
其中正确结论的个数是( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
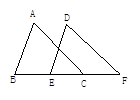
11. 吴京导演的《战狼2》创下了56.8亿票房神话,将数据56.8亿用科学记数法表示为 .12. 在函数y= +(x﹣4)0中,自变量x的取值范围是 .13. 如图:∠ABC=∠DEF,AB=DE,要证明△ABC≌△DEF,需要添加一个条件为(只添加一个条件即可);
 14. CD是以AB为直径的⊙O的一条弦,CD AB , ∠CAD=40°,若⊙O的半径为9cm , 则阴影部分的面积为cm2 .
14. CD是以AB为直径的⊙O的一条弦,CD AB , ∠CAD=40°,若⊙O的半径为9cm , 则阴影部分的面积为cm2 . 15. 在矩形 中, ,点P为线段 垂直平分线上一点,且 ,则 的长是 .16. 直角三角形的两条边的长分别是 和 ,以直角边所在的直线为轴,将三角形旋转一周,所得几何体的底面积是 .17. 如图,放置的 ,都是边长为4的等边三角形,点A在x轴上,点 ,都在正比例函数 的图象l上,则点 的坐标是 .
15. 在矩形 中, ,点P为线段 垂直平分线上一点,且 ,则 的长是 .16. 直角三角形的两条边的长分别是 和 ,以直角边所在的直线为轴,将三角形旋转一周,所得几何体的底面积是 .17. 如图,放置的 ,都是边长为4的等边三角形,点A在x轴上,点 ,都在正比例函数 的图象l上,则点 的坐标是 .
三、解答题
-
18.(1)、计算: .(2)、分解因式: .19. 解方程:3x(x﹣1)=2﹣2x.20. 如图, 是 的直径, 是 的弦,过点 作 的切线,交 的延长线于点 ,过点 作 于点 ,交 的延长线于点 .
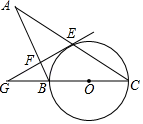 (1)、求证: ;(2)、若 , ,求 的半径.21. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动。为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它"四种类型的设备对学生做了一次抽样调查。调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)、求证: ;(2)、若 , ,求 的半径.21. 受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动。为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它"四种类型的设备对学生做了一次抽样调查。调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题: (1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.22. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)、补全条形统计图;(2)、若该校共有1500名学生,估计全校用手机上网课的学生共有名;(3)、在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.22. 甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题: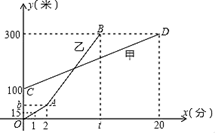 (1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间时,甲、乙两人距地面的高度差为70米?23. 综合与实践﹣﹣﹣折叠中的数学
(1)、甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米;(2)、若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间时,甲、乙两人距地面的高度差为70米?23. 综合与实践﹣﹣﹣折叠中的数学在学习完特殊的平行四边形之后,某学习小组针对矩形中的折叠问题进行了研究.
问题背景:
在矩形ABCD中,点E、F分别是BC、AD 上的动点,且BE=DF,连接EF,将矩形ABCD沿EF折叠,点C落在点C′处,点D落在点D′处,射线EC′与射线DA相交于点M.
 (1)、猜想与证明:如图1,当EC′与线段AD交于点M时,判断△MEF的形状并证明你的结论;(2)、操作与画图:当点M与点A重合时,请在图2中作出此时的折痕EF和折叠后的图形(要求:尺规作图,不写作法,保留作图痕迹,标注相应的字母);(3)、操作与探究:如图3,当点M在线段DA延长线上时,线段C′D'分别与AD,AB交于P,N两点时,C′E与AB交于点Q,连接MN 并延长MN交EF于点O.
(1)、猜想与证明:如图1,当EC′与线段AD交于点M时,判断△MEF的形状并证明你的结论;(2)、操作与画图:当点M与点A重合时,请在图2中作出此时的折痕EF和折叠后的图形(要求:尺规作图,不写作法,保留作图痕迹,标注相应的字母);(3)、操作与探究:如图3,当点M在线段DA延长线上时,线段C′D'分别与AD,AB交于P,N两点时,C′E与AB交于点Q,连接MN 并延长MN交EF于点O.求证:MO⊥EF 且MO平分EF;
(4)、若AB=4,AD=4 ,在点E由点B运动到点C的过程中,点D'所经过的路径的长为 .24. 综合与探究如图,抛物线 与x轴交于 、 两点,与y轴交于点C .
 (1)、求抛物线解析式;(2)、抛物线对称轴上存在一点H , 连接 、 ,当 值最大时,点H坐标为 .(3)、若抛物线上存在一点 ,当 时,求点P坐标;(4)、若点M是该抛物线对称轴上一点,点N是平面内一点,以A、C、M、N为顶点的四边形是矩形,请直接写出点N坐标.
(1)、求抛物线解析式;(2)、抛物线对称轴上存在一点H , 连接 、 ,当 值最大时,点H坐标为 .(3)、若抛物线上存在一点 ,当 时,求点P坐标;(4)、若点M是该抛物线对称轴上一点,点N是平面内一点,以A、C、M、N为顶点的四边形是矩形,请直接写出点N坐标.