黑龙江省哈尔滨市平房区2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. ﹣2的倒数为( )A、﹣ B、 C、2 D、12. 下列运算一定正确的是( )A、x3+x3=x6 B、x3•x4=x12 C、(x3)4=x12 D、(x﹣y)2=x2﹣y23. 下列图形是中心对称图形,但不是轴对称图形的是( )A、平行四边形 B、正方形 C、矩形 D、菱形4. 七个大小相同的正方体搭成的几何体如图所示,其主视图是( )
 A、
A、 B、
B、 C、
C、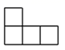 D、
D、 5. 如图,在 中, , ,将 绕点 逆时针旋转75°,得到 ,则 的度数为( )
5. 如图,在 中, , ,将 绕点 逆时针旋转75°,得到 ,则 的度数为( )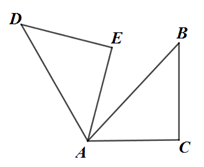 A、75° B、90° C、120° D、165°6. 如图, 为 的直径,过圆上一点 作 的切线,交 的延长线于点 ,连接 ,若 ,则 的度数为( )
A、75° B、90° C、120° D、165°6. 如图, 为 的直径,过圆上一点 作 的切线,交 的延长线于点 ,连接 ,若 ,则 的度数为( ) A、15° B、20° C、25° D、30°7. 将抛物线 向右平移1个单位长度,再向下平移3个单位长度,所得到的抛物线为( )A、 B、 C、 D、8. 方程 的解为( )A、 B、 C、 D、9. 九年一班有12名同学报名参加校园踢毽子比赛,其中8名男生,4名女生,体育委员随机抽出一名同学代表班级参加比赛,则抽出的同学是女生的概率是( )A、 B、 C、 D、10. 如图,在 中,点 、 分别在 、 上, ,点 在 的延长线上, ,则下列结论错误的是( )
A、15° B、20° C、25° D、30°7. 将抛物线 向右平移1个单位长度,再向下平移3个单位长度,所得到的抛物线为( )A、 B、 C、 D、8. 方程 的解为( )A、 B、 C、 D、9. 九年一班有12名同学报名参加校园踢毽子比赛,其中8名男生,4名女生,体育委员随机抽出一名同学代表班级参加比赛,则抽出的同学是女生的概率是( )A、 B、 C、 D、10. 如图,在 中,点 、 分别在 、 上, ,点 在 的延长线上, ,则下列结论错误的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 将数20210000用科学记数法表示为 .12. 函数 中,自变量x的取值范围是.13. 计算 的结果是 .14. 把多项式 分解因式的结果是 .15. 已知反比例函数 的图像经过点 ,则 的值为 .16. 抛物线y=﹣2(x+1)2﹣3的顶点坐标是 .17. 不等式组 的解集是 .18. 一个扇形的面积是 ,圆心角是120°,则此扇形的半径是cm.19. 已知等边三角形 , ,点 在 上,过点 作 的垂线,交射线 于点 ,交射线 于点 ,若 ,则 的长为 .20. 如图,在△ABC中,AB=BC=2 ,AE⊥BC , 垂足为点E , 延长AE至点D , 使AD=AB , 连接CD、BD , 若∠ACD=90°,则BD的长为 .

三、解答题
-
21. 先化简,再求代数式 的值,其中 .22. 如图,方格纸中每个小正方形的边长均为小,线段 、 的端点在小正方形的顶点上.
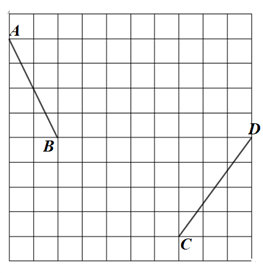
⑴在图中画一个以 为腰的等腰直角三角形 ,点 在小正方形的顶点上;
⑵在图中画一个以 为边的菱形 ,点 , 在小正方形的顶点上,且面积为20,连接 ,并直接写出线段 的长.
23. 为了解学生线上学习的需求,虹友中学随机对部分学生进行了“你最喜欢哪类在线学习方式”(必选且只选一类)的调查,并根据调查结果,绘制成如图所示的不完整的条形统计图,其中最喜欢“线上听课”的学生人数占所调查人数的45%.请你根据图中提供的信息回答下列问题: (1)、在这次调查中,一共调查了多少名学生?(2)、通过计算将条形统计图补充完整;(3)、若虹友中学共有1200名学生,请你估计该校最喜欢“线上答题”方式的学生有多少名?24. 已知:平行四边形 ,过点 、 分别作 、 的垂线,交 于 、 两点,连接 、 .
(1)、在这次调查中,一共调查了多少名学生?(2)、通过计算将条形统计图补充完整;(3)、若虹友中学共有1200名学生,请你估计该校最喜欢“线上答题”方式的学生有多少名?24. 已知:平行四边形 ,过点 、 分别作 、 的垂线,交 于 、 两点,连接 、 .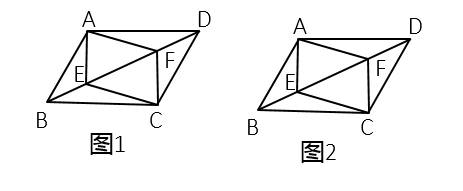 (1)、如图1,求证:四边形 是平行四边形;(2)、如图2,当点 为 中点时,请直接写出图2中与四边形 面积相等的所有三角形.25. 为了丰富学生的大课间活动,振海中学到体育用品商店购买篮球和足球,若购买2个篮球和3个足球共需600元,购买3个篮球和1个足球共需550元.(1)、求篮球和足球的单价分别是多少元?(2)、振海中学决定购买篮球和足球共20个,经商议,体育用品商店决定篮球单价打八折,足球单价不变,若总费用不超过2200元,那么该校最多可以购买多少个篮球?26. 已知:△ABC内接于⊙O , 过点B作BD⊥AC , 垂足为点D , ∠BAC=2∠DBC .
(1)、如图1,求证:四边形 是平行四边形;(2)、如图2,当点 为 中点时,请直接写出图2中与四边形 面积相等的所有三角形.25. 为了丰富学生的大课间活动,振海中学到体育用品商店购买篮球和足球,若购买2个篮球和3个足球共需600元,购买3个篮球和1个足球共需550元.(1)、求篮球和足球的单价分别是多少元?(2)、振海中学决定购买篮球和足球共20个,经商议,体育用品商店决定篮球单价打八折,足球单价不变,若总费用不超过2200元,那么该校最多可以购买多少个篮球?26. 已知:△ABC内接于⊙O , 过点B作BD⊥AC , 垂足为点D , ∠BAC=2∠DBC . (1)、如图1,求证:AB=AC;(2)、如图2,点E在AC上,连接BE , F为BE中点,连接CF , ∠ECF=∠BAC , 求证:AB=2CF;(3)、如图3,在(2)的条件下,延长BE、BD分别交⊙O于点G、H , AG、CH的延长线相交于点K , 连接OE , 若OE= ,∠AKC=90°,求线段HK的长.27. 在平面直角坐标系xOy中,直线AB交x轴于点B , 交y轴于点A , 直线AC交x轴于点C , AB=AC , 点C的坐标是(3,0).
(1)、如图1,求证:AB=AC;(2)、如图2,点E在AC上,连接BE , F为BE中点,连接CF , ∠ECF=∠BAC , 求证:AB=2CF;(3)、如图3,在(2)的条件下,延长BE、BD分别交⊙O于点G、H , AG、CH的延长线相交于点K , 连接OE , 若OE= ,∠AKC=90°,求线段HK的长.27. 在平面直角坐标系xOy中,直线AB交x轴于点B , 交y轴于点A , 直线AC交x轴于点C , AB=AC , 点C的坐标是(3,0). (1)、如图1,求点B坐标;(2)、如图2,点D在线段AB上,点E在线段AC延长线上,连接DE交OC于点F , DF=EF , 过点E作EH⊥x轴,垂足为点H , 设点F的横坐标为t , BH长为d , 求d与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,在BA的延长线上取一点K , 使AK=CE , 连接CK、FK , 过点D的直线交x轴于点G , 交直线AC于点M , 连接BM、GK , 若∠BMG=∠FKC , BM∥KF , △CKG的面积为12,求直线GK的解析式.
(1)、如图1,求点B坐标;(2)、如图2,点D在线段AB上,点E在线段AC延长线上,连接DE交OC于点F , DF=EF , 过点E作EH⊥x轴,垂足为点H , 设点F的横坐标为t , BH长为d , 求d与t的函数关系式(不要求写出自变量t的取值范围);(3)、如图3,在(2)的条件下,在BA的延长线上取一点K , 使AK=CE , 连接CK、FK , 过点D的直线交x轴于点G , 交直线AC于点M , 连接BM、GK , 若∠BMG=∠FKC , BM∥KF , △CKG的面积为12,求直线GK的解析式.