河北省唐山市玉田县2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 实数 的值是( )A、 B、 C、1 D、-12. 下列各式:① ,② ,③ ,从左到右的变形中,属于因式分解的是( )A、② B、①② C、①③ D、②③3. 已知:如图,正方形面积为8,其边长是 ,则关于 的结论中正确的是( )
 A、正方形的对角线长是4 B、8的平方根是 C、 是有理数 D、 不能在数轴上表示4. 我国2020年国内生产总值大约 万亿元.数据“101万亿”用科学记数法表示为( )A、 B、 C、 D、5. 如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A、正方形的对角线长是4 B、8的平方根是 C、 是有理数 D、 不能在数轴上表示4. 我国2020年国内生产总值大约 万亿元.数据“101万亿”用科学记数法表示为( )A、 B、 C、 D、5. 如图,五边形ABCDE中,AB∥CD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )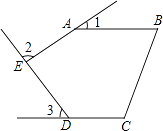 A、90° B、180° C、210° D、270°6. 计算: ,则 等于( )A、-1 B、1 C、 D、7. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )
A、90° B、180° C、210° D、270°6. 计算: ,则 等于( )A、-1 B、1 C、 D、7. 如图,AB是半圆的直径,O为圆心,C是半圆上的点,D是 上的点,若∠BOC=40°,则∠D的度数为( )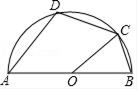 A、100° B、110° C、120° D、130°8. 小明在计算一组数据的方差时,列出的公式如下: ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是09. 证明:平行四边形的对角线互相平分.
A、100° B、110° C、120° D、130°8. 小明在计算一组数据的方差时,列出的公式如下: ,根据公式信息,下列说法中,错误的是( )A、数据个数是5 B、数据平均数是8 C、数据众数是8 D、数据方差是09. 证明:平行四边形的对角线互相平分.已知:如图,四边形 是平行四边形,对角线 、 相交于点 .

求证: , ,嘉琪的证明过程如下:
证明:从四边形 是平行四边形
∴_____________________________
∴ ,
∴
∴ ,
上面证明过程中,“________”应补充的步骤是( )
A、 , B、 , C、 , D、 ﹐10. 关于x的一元二次方程 有两个不相等的实数根,则a的取值范围是( )A、 B、 C、 D、 且11. 如图,点 , , 在 上, 是 的一条弦,则 的值是( )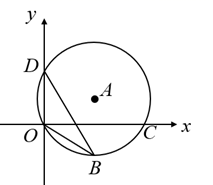 A、 B、 C、 D、12. 由7个大小相同的正方体搭成的几何体如图所示,则以下结论:①主视图既是轴对称图形,又是中心对称图形;②俯视图是中心对称图形;③左视图不是中心对称图形;④俯视图和左视图都不是轴对称图形,其中符合题意结论是( )
A、 B、 C、 D、12. 由7个大小相同的正方体搭成的几何体如图所示,则以下结论:①主视图既是轴对称图形,又是中心对称图形;②俯视图是中心对称图形;③左视图不是中心对称图形;④俯视图和左视图都不是轴对称图形,其中符合题意结论是( )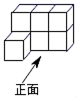 A、①③ B、①④ C、②③ D、②④13. 如图,在 中, , ,分别以 、 为圆心,大于 的长为半径画弧,两弧相交于点 、 .作直线 ,交 于点 ;同理作直线 交 于点 ,若 ,则 的长为( )
A、①③ B、①④ C、②③ D、②④13. 如图,在 中, , ,分别以 、 为圆心,大于 的长为半径画弧,两弧相交于点 、 .作直线 ,交 于点 ;同理作直线 交 于点 ,若 ,则 的长为( )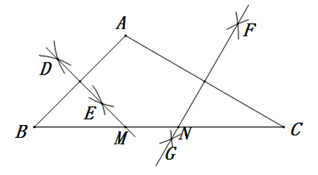 A、1 B、 C、3 D、14. 若 ,则 的值是( )A、100 B、105 C、200 D、20515. 在《类比探究菱形的有关问题》这节网课中,老师给出了如下画菱形的步骤,请问这么画的依据是( )
A、1 B、 C、3 D、14. 若 ,则 的值是( )A、100 B、105 C、200 D、20515. 在《类比探究菱形的有关问题》这节网课中,老师给出了如下画菱形的步骤,请问这么画的依据是( )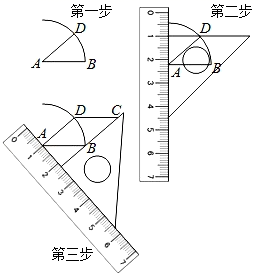 A、四条边都相等的四边形是菱形 B、两组对边分别相等的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 C、两组对边分别平行的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形,两条对角线互相垂直的平行四边形是菱形16. 如图,现要在抛物线 上找点 ,针对b的不同取值,所找点P的个数,三人的说法如下,
A、四条边都相等的四边形是菱形 B、两组对边分别相等的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 C、两组对边分别平行的四边形是平行四边形,有一组邻边相等的平行四边形是菱形 D、两组对边分别平行的四边形是平行四边形,两条对角线互相垂直的平行四边形是菱形16. 如图,现要在抛物线 上找点 ,针对b的不同取值,所找点P的个数,三人的说法如下,甲:若 ,则点P的个数为0;
乙:若 ,则点P的个数为1;
丙:若 ,则点P的个数为1.
下列判断正确的是( )
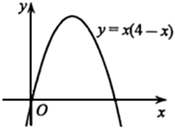 A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对
A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对二、填空题
-
17. 分式方程: 的解为 .18. 如图,四边形ABCD是平行四边形,E为BC边的中点,DE、AC相交于点F,若△CEF的面积为6,则△ADF的面积为 .

三、解答题
-
19. 如图,矩形 的顶点 与原点 重合,矩形的周长为 ,矩形的顶点 , 分别位于 轴和 轴的正半轴上,顶点 位于第一象限,函数 的图象经过点 .
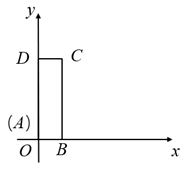 (1)、当 时,则 ;(2)、若(1)中 的值仍然成立,猜想反比例函数 可能经过的另一个整点C的坐标为;(3)、当函数 的图象上方有且只有 个整点 时, 的取值范围是 .20. 对于实数 、 ,定义关于“ ”的一种运算: .例如 .(1)、求 的值;(2)、若 , ,求 和 的值.21. 如图,甲、乙两张卡片上均有一个系数为整数的多项式,其中乙中二次项系数因为被污染看不清楚.
(1)、当 时,则 ;(2)、若(1)中 的值仍然成立,猜想反比例函数 可能经过的另一个整点C的坐标为;(3)、当函数 的图象上方有且只有 个整点 时, 的取值范围是 .20. 对于实数 、 ,定义关于“ ”的一种运算: .例如 .(1)、求 的值;(2)、若 , ,求 和 的值.21. 如图,甲、乙两张卡片上均有一个系数为整数的多项式,其中乙中二次项系数因为被污染看不清楚.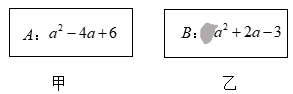 (1)、嘉嘉认为污染的数为-3,计算“ ”的结果;(2)、若 ,淇淇认为存在一个整数,可以使得“ ”的结果是整数,请你求出满足题意的被污染的这个数.22. 疫情期间,游海中学进行了一次线上数学学情调查,九(1)班数学李老师对成绩进行分析,制作如下的频数分布表和频数分布直方图.60到70之间学生成绩尚未统计,根据情况画出的扇形图如图.请解答下列问题:
(1)、嘉嘉认为污染的数为-3,计算“ ”的结果;(2)、若 ,淇淇认为存在一个整数,可以使得“ ”的结果是整数,请你求出满足题意的被污染的这个数.22. 疫情期间,游海中学进行了一次线上数学学情调查,九(1)班数学李老师对成绩进行分析,制作如下的频数分布表和频数分布直方图.60到70之间学生成绩尚未统计,根据情况画出的扇形图如图.请解答下列问题:类别
分数段
频数(人数)
A
a
B
16
C
24
D
6
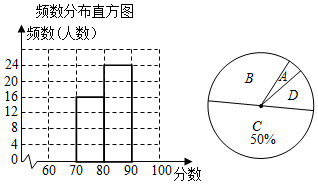 (1)、完成频数分布表,a= ▲ , B类圆心角= ▲ °,并补全频数分布直方图;(2)、全校九年级共有720名学生全部参加此次测试,估计该校成绩 范围内的学生有多少人?(3)、九(1)班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流,已知这6人中有两名是无家长管理的留守学生,求恰好只选中其中一名留守学生进行经验交流的概率.23. 如图, , , 轴,与直线 交于点 , 轴于点 , 是折线 上一动点.设过点 , 的直线为 .
(1)、完成频数分布表,a= ▲ , B类圆心角= ▲ °,并补全频数分布直方图;(2)、全校九年级共有720名学生全部参加此次测试,估计该校成绩 范围内的学生有多少人?(3)、九(1)班数学老师准备从D类优生的6人中随机抽取两人进行线上学习经验交流,已知这6人中有两名是无家长管理的留守学生,求恰好只选中其中一名留守学生进行经验交流的概率.23. 如图, , , 轴,与直线 交于点 , 轴于点 , 是折线 上一动点.设过点 , 的直线为 .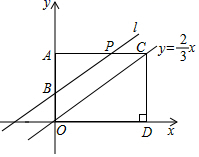 (1)、点 的坐标为;(2)、若直线 所在的函数随 的增大而减少,则 的取值范围是;(3)、若动点 在 上运动, 与 相似时,求此时直线 的解析式.24. 如图, 是半圆 的直径, 是半圆 上不同于 、 两点的任意一点, 是半圆 上一动点, 与 相交于点 , 是半圆 所在圆的切线,与 的延长线相交于点 .
(1)、点 的坐标为;(2)、若直线 所在的函数随 的增大而减少,则 的取值范围是;(3)、若动点 在 上运动, 与 相似时,求此时直线 的解析式.24. 如图, 是半圆 的直径, 是半圆 上不同于 、 两点的任意一点, 是半圆 上一动点, 与 相交于点 , 是半圆 所在圆的切线,与 的延长线相交于点 .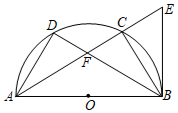 (1)、若 ,求证: ;(2)、若 , , .求 ;(答案保留 )(3)、若 , 为 的中点,点 从 移动到 时,请直接写出点 移动的长度.(答案保留 )25. 某商场经销一种商品,已知其每件进价为40元.现在每件售价为70元,每星期可卖出500件.该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件.设调查价格后每星期的销售利润为W元.(1)、设该商品每件涨价x(x为正整数)元,
(1)、若 ,求证: ;(2)、若 , , .求 ;(答案保留 )(3)、若 , 为 的中点,点 从 移动到 时,请直接写出点 移动的长度.(答案保留 )25. 某商场经销一种商品,已知其每件进价为40元.现在每件售价为70元,每星期可卖出500件.该商场通过市场调查发现:若每件涨价1元,则每星期少卖出10件;若每件降价1元,则每星期多卖出m(m为正整数)件.设调查价格后每星期的销售利润为W元.(1)、设该商品每件涨价x(x为正整数)元,①若x=5,则每星期可卖出 ▲ 件,每星期的销售利润为 ▲ 元;
②当x为何值时,W最大,W的最大值是多少?
(2)、设该商品每件降价y(y为正整数)元,①写出W与y的函数关系式,并通过计算判断:当m=10时每星期销售利润能否达到(1)中W的最大值;
②若使y=10时,每星期的销售利润W最大,直接写出W的最大值为 ▲ .
(3)、若每件降价5元时的每星期销售利润,不低于每件涨价15元时的每星期销售利润,求m的取值范围.26. 如图,在 中,已知 , 于 ,点 、 分别从 、 两点同时出发,其中点 沿 向终点 运动,速度为 ;点 沿 、 向终点 运动,速度为 ,设它们的运动时间为 .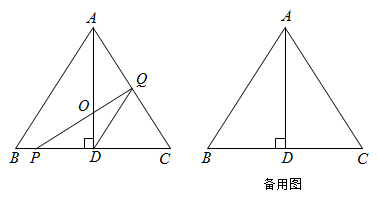 (1)、求 为何值时, ;(2)、设 的面积为 ,当 时,解决下列问题:
(1)、求 为何值时, ;(2)、设 的面积为 ,当 时,解决下列问题:①求 与 的函数关系式;
②求证: 平分 的面积;
(3)、探索以 为直径的圆与 的位置关系,请直接写出相应位置关系的 的取值范围.