河北省沧州市南皮县2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 如图,在直线 上的点是( )
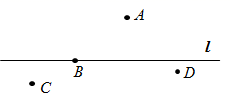 A、点A B、点B C、点C D、点D2. 我国第十四个五年规划和2035年远景目标纲要中阐释了“坚持农业农村优先发展,全面推进乡村振兴”的具体目标:坚持最严格的耕地保护制度,实施高标准农田建设工程,建成 亿亩集中连片高标准农田,下列关于 亿的说法正确的是( )A、 亿是精确到亿位 B、 亿是精确到十亿位 C、 亿用科学记数法表示为 ,则 ,n=9 D、 亿用科学记数法表示为 ,则 ,3. 计算: ( )A、 B、 C、 D、4. 将一副三角板按如图所示的方式摆放,则∠1=( )
A、点A B、点B C、点C D、点D2. 我国第十四个五年规划和2035年远景目标纲要中阐释了“坚持农业农村优先发展,全面推进乡村振兴”的具体目标:坚持最严格的耕地保护制度,实施高标准农田建设工程,建成 亿亩集中连片高标准农田,下列关于 亿的说法正确的是( )A、 亿是精确到亿位 B、 亿是精确到十亿位 C、 亿用科学记数法表示为 ,则 ,n=9 D、 亿用科学记数法表示为 ,则 ,3. 计算: ( )A、 B、 C、 D、4. 将一副三角板按如图所示的方式摆放,则∠1=( )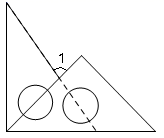 A、 B、 C、 D、5. 对于:
A、 B、 C、 D、5. 对于:① ;② ;③ ;④ .其中因式分解正确的是( )
A、①③ B、②③ C、①④ D、②④6. 如图,是某几何体的展开图, ,则 ( )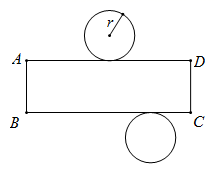 A、2 B、4 C、8 D、167. 下列关于 的方程中,一定有两个不相等实数根的是( )A、 B、 C、 D、8. 嘉淇所在的社团,两年来人员没有变化,嘉淇计算了目前社团人员年龄的方差为1,则两年前该社团人员年龄的方差为( )A、1 B、2 C、3 D、59. 如图,是一个闭合电路,其电源电压为定值,电流 是电阻 的反比例函数,当 时, ,若电阻 增大 ,则电流 为( )
A、2 B、4 C、8 D、167. 下列关于 的方程中,一定有两个不相等实数根的是( )A、 B、 C、 D、8. 嘉淇所在的社团,两年来人员没有变化,嘉淇计算了目前社团人员年龄的方差为1,则两年前该社团人员年龄的方差为( )A、1 B、2 C、3 D、59. 如图,是一个闭合电路,其电源电压为定值,电流 是电阻 的反比例函数,当 时, ,若电阻 增大 ,则电流 为( ) A、 B、 C、 D、10. 如图,在 中, ,以点 为圆心,任意长为半径画弧,分别与 , 交于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧在 内部相交于点 ,作射线 ,交 边于点 .若cos ,则 的长为( )
A、 B、 C、 D、10. 如图,在 中, ,以点 为圆心,任意长为半径画弧,分别与 , 交于点 , ,再分别以点 , 为圆心,大于 的长为半径画弧,两弧在 内部相交于点 ,作射线 ,交 边于点 .若cos ,则 的长为( )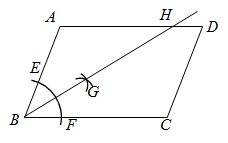 A、2 B、3 C、4 D、611. 不等式组 ,的解集为 ,则 的取值不可能是( )A、-4 B、-3 C、-2 D、-112. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )
A、2 B、3 C、4 D、611. 不等式组 ,的解集为 ,则 的取值不可能是( )A、-4 B、-3 C、-2 D、-112. 如图,在 的正方形网格图中,小正方形的边长为1, 的顶点均在格点上,则下列关于 的说法错误的是( )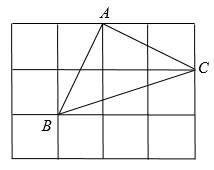 A、是直角三角形 B、tam C、面积为 D、 边上的高为13. 在一个大正方形上,按如图所示的方式粘贴面积分别为12,10的两个小正方形,粘贴后,这两个小正方形重合部分的面积为3,则空白部分的面积为( )
A、是直角三角形 B、tam C、面积为 D、 边上的高为13. 在一个大正方形上,按如图所示的方式粘贴面积分别为12,10的两个小正方形,粘贴后,这两个小正方形重合部分的面积为3,则空白部分的面积为( )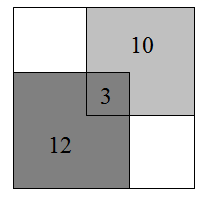 A、8 B、19 C、 D、14. 如图,M是 上一个定点,将直角三角板的 角顶点与点M重合,两边与 相交,设交点为A,B,绕点M顺时针旋转三角板,直至其中一个交点与点M重合时停止旋转,设 ,旋转角为 ,如图所示能反映 与 关系的为( )
A、8 B、19 C、 D、14. 如图,M是 上一个定点,将直角三角板的 角顶点与点M重合,两边与 相交,设交点为A,B,绕点M顺时针旋转三角板,直至其中一个交点与点M重合时停止旋转,设 ,旋转角为 ,如图所示能反映 与 关系的为( )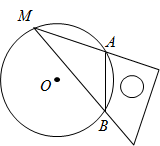 A、
A、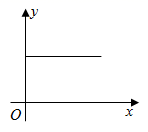 B、
B、 C、
C、 D、
D、 15. 如图, 中, , 是中线, 是 上一点,作射线 ,交 于点 ,若 ,则 ( )
15. 如图, 中, , 是中线, 是 上一点,作射线 ,交 于点 ,若 ,则 ( ) A、2 B、2.5 C、3 D、3.516. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )
A、2 B、2.5 C、3 D、3.516. 如图,矩形 中, , ,抛物线 的顶点 在矩形 内部或其边上,则 的取值范围是( )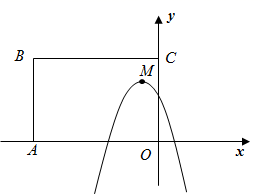 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 计算: .18. 对于代数式 ,(m为整式).(1)、当 时,化简 的结果为;(2)、若化简M的结果为 ,则 .19. 如图,在 中, , , , 是 边上一点,连接 ,将 绕点 顺时针旋转,得到 ,点 , 的对应点分别是点E,D,点E在AB边上.
 (1)、若 是 的中点,则DB=;(2)、若 ,则点D到 的距离为 .
(1)、若 是 的中点,则DB=;(2)、若 ,则点D到 的距离为 .三、解答题
-
20. 已知:整式 , .(1)、化简 ;(2)、若无论 为何值, ( 为常数)的值都是正数,求 的取值范围.21. 如图,数轴上,点 , 表示的数分别为 , ,点 为负半轴上任意一点,它表示的数为 .
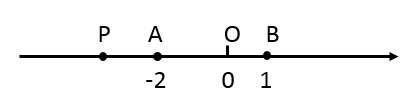 (1)、计算 的值;(2)、在 中,其中一个数是另两个数的平均数,求 的值;(3)、嘉琪认为:当 时, ,则以 的长为边长不能构成三角形.若以 的长为边长能构成三角形,请直接写出 的取值范围.22. 某校九年级共有360名学生,某次数学测验后,小明随机抽取了40名学生的成绩进行统计,并绘制了频数分布直方图(数据分成5个组:① ,② ,③ ,④ ,⑤ ),如图.
(1)、计算 的值;(2)、在 中,其中一个数是另两个数的平均数,求 的值;(3)、嘉琪认为:当 时, ,则以 的长为边长不能构成三角形.若以 的长为边长能构成三角形,请直接写出 的取值范围.22. 某校九年级共有360名学生,某次数学测验后,小明随机抽取了40名学生的成绩进行统计,并绘制了频数分布直方图(数据分成5个组:① ,② ,③ ,④ ,⑤ ),如图.
已知成绩在80≤x<90这一组的是:80,81,82,82,83,85,86,86,86,87,88,89.
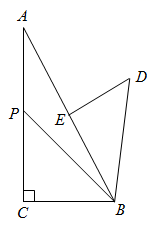
(1)、在 这一组中,这些数据的众数为;(2)、求抽取的这40名学生的成绩的中位数;(3)、在 , 这两组中随机抽取一个成绩,记录下来再放回,然后在这两组中随机抽取一个成绩,用画树状图法求两次抽到的成绩都在 这一组的概率;(4)、请你估计该校九年级这360名学生中,数学成绩 的有多少人.23. 如图,射线 , 是 上的一点,以 为圆心, 长为半径,在 上方作半圆 , 与半圆相切于点 ,交 于点 , 于点 . (1)、求证: ;(2)、若 ,
(1)、求证: ;(2)、若 ,①判断点 与半圆 所在圆的位置关系,并说明理由;
②若 ,直接写出阴影部分的面积.
24. 如图,直线 与 轴交于点 ,与 轴交于点 ,点 为射线 上的一点(点 不与点 重合), 是 的中线,点 , 关于 对称,设点 的横坐标为 . (1)、求点 , 的坐标,若 ,求 所在直线的解析式;(2)、若 ,求 的值;(3)、若点 在 轴下方,直接写出 的取值范围.25. 某水果商计划从生产基地运回一批水果,所需运费为基础运费与载重运费两部分的和,基础运费为每次500元,载重运费为每吨每小时6元,经验表明,若运回水果20吨,路上恰好需要6小时,运回的水果全部批发完后,每吨水果能获得毛利润478元;若运输时每增加2吨水果,路上就会延长1小时,每延长1小时,每吨水果的毛利润会降低20元.设运回水果为 吨 ,路上所用时间为 小时,所需运费为 元,全部批发后水果商获得总净利润为 元(净利润=毛利润﹣所需运费).(不考虑损耗)(1)、用含 的式子表示 为;(2)、①求 与 的函数关系式;
(1)、求点 , 的坐标,若 ,求 所在直线的解析式;(2)、若 ,求 的值;(3)、若点 在 轴下方,直接写出 的取值范围.25. 某水果商计划从生产基地运回一批水果,所需运费为基础运费与载重运费两部分的和,基础运费为每次500元,载重运费为每吨每小时6元,经验表明,若运回水果20吨,路上恰好需要6小时,运回的水果全部批发完后,每吨水果能获得毛利润478元;若运输时每增加2吨水果,路上就会延长1小时,每延长1小时,每吨水果的毛利润会降低20元.设运回水果为 吨 ,路上所用时间为 小时,所需运费为 元,全部批发后水果商获得总净利润为 元(净利润=毛利润﹣所需运费).(不考虑损耗)(1)、用含 的式子表示 为;(2)、①求 与 的函数关系式;②若某一次运费为1652元,则这次运回了多少吨水果?
(3)、一次运回多少吨水果,水果商获得的总的净利润最大?总的最大净利润是多少?26. 如图1和图2,在矩形 中, , ,点K在 边上,点M, 分别在AB, 边上,且 ,点 从点M出发沿折线 匀速运动,点 在 上随 移动,且始终保持 ;点 从点 出发沿 匀速运动,点 , 同时出发,点 的速度是点 的一半,点 到达点 停止,点 随之停止.设点 移动的路程为 .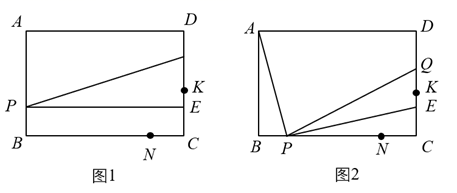 (1)、当点 在 上时,求点 , 的距离(用含 的式子表示);(2)、当 时,求 的值;(3)、若 ,求 的取值范围;(4)、已知点 从点 到点 再到点 共用时 秒,若 ,请直接写出点K在线段 上(包括端点)的总时长.
(1)、当点 在 上时,求点 , 的距离(用含 的式子表示);(2)、当 时,求 的值;(3)、若 ,求 的取值范围;(4)、已知点 从点 到点 再到点 共用时 秒,若 ,请直接写出点K在线段 上(包括端点)的总时长.