北京市西城区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. “沿着高速看中国”,镶嵌于正阳门前的“中国公路零公里点”标志牌见证了中国高速公路从“零”出发的跨越式发展.截至2020年底,我国高速公路总里程己达160000公里.将160000用科学记数法表示应为( )
 A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、
A、 B、 C、 D、2. 下列图形中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 以下变形正确的是( )A、 B、 C、 D、4. 如图是某几何体的表面展开图,则这个几何体是( )
3. 以下变形正确的是( )A、 B、 C、 D、4. 如图是某几何体的表面展开图,则这个几何体是( ) A、正三棱柱 B、正方体 C、圆柱 D、圆锥5. 半径为 ,圆心角为 的扇形的面积等于( )A、 B、 C、 D、6. 若相似三角形的相似比为1:4,则面积比为( )A、1:16 B、16:1 C、1:4 D、1:27. 密云水库是首都北京重要水源地,水源地生态保护对保障首都水源安全及北京市生态和城市可持线发展具有不可替代的作用.以下是1986-2020年密云水库水体面积和年降水量变化图:
A、正三棱柱 B、正方体 C、圆柱 D、圆锥5. 半径为 ,圆心角为 的扇形的面积等于( )A、 B、 C、 D、6. 若相似三角形的相似比为1:4,则面积比为( )A、1:16 B、16:1 C、1:4 D、1:27. 密云水库是首都北京重要水源地,水源地生态保护对保障首都水源安全及北京市生态和城市可持线发展具有不可替代的作用.以下是1986-2020年密云水库水体面积和年降水量变化图:
对于现有数据有以下结论:
①2004年的密云水库水体面积最小,仅约为 ②2015-2020年,密云水库的水体面积昰持续增加趋势.表明水资源储备增多;③在1986-2020年中,2020年的密云水库水体面积最大,约为 ④在1986-2020年中,密云水库年降水量最大的年份,水体面积也最大其中结论正确的是( )
A、②③ B、②④ C、①②③ D、①②④8. 如图, ,点B在射线 上, .点P在射线 上运动(点P不与点A重合),连接 ,以点B为圆心, 为半径作弧交射线 于点Q , 连接 .若 ,则下列图象中,能表示y与x的函数关系的图象大致是( )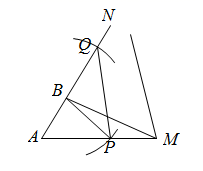 A、
A、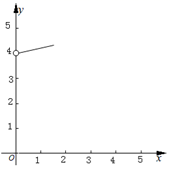 B、
B、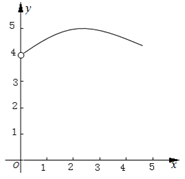 C、
C、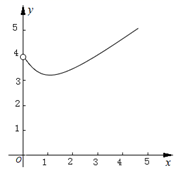 D、
D、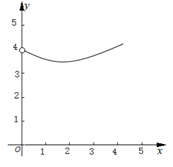
二、填空题
-
9. 若 在实数范围内有意义,则实数x的取值范围是.10. 因式分解: .11. 50件外观相同的产品中有2件不合格,现从中随机抽取1件进行捡测,抽到不合格产品的概率是 .12. 在平面直角坐标系 中,直线 与x轴的交点的坐标为 .13. 如图,直线l为线段 的垂直平分线,垂足为C , 直线l上的两点E , F位于 异侧(E , F两点不与点C重合).只需添加一个条件即可证明 ,这个条件可以是 .
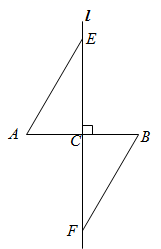 14. 图1是用一种彭罗斯瓷砖平铺成的图案,它的基础部分是“风筝”和“飞镖”两郎分,图2中的“风筝”和“飞镖”是由图3所示的特殊菱形制作而成.在菱形 中, ,在对角线 上截取 ,连按 , ,可将菱形分割为“风筝”(凸四边 )和“飞镖”(凹四边形 )两部分,则图2中的 °.
14. 图1是用一种彭罗斯瓷砖平铺成的图案,它的基础部分是“风筝”和“飞镖”两郎分,图2中的“风筝”和“飞镖”是由图3所示的特殊菱形制作而成.在菱形 中, ,在对角线 上截取 ,连按 , ,可将菱形分割为“风筝”(凸四边 )和“飞镖”(凹四边形 )两部分,则图2中的 °.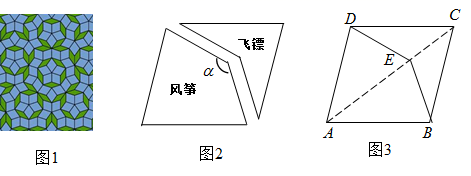 15. 从1,2,3,4,5中选择四个数字组成四位数 ,其中a , b , c , d分别代表千位、百位、十位、个位数字.若要求这个四位数同时满足以下条件:① 是偶数;② ;③ ,请写出一个符合要求的数 .16. 如图,在平面直角坐标系 中,已知直线 ,直线 ,直线 交 于点 ,交 于点 ,过点 作y轴的垂线交 于点 ,过点 作x轴的垂线,交 于点 ,过点 作y轴的垂线交 于点 ,…,按此方式进行下去,则 的坐标为 , 的坐标为(用含n的式子表示,n为正整数).
15. 从1,2,3,4,5中选择四个数字组成四位数 ,其中a , b , c , d分别代表千位、百位、十位、个位数字.若要求这个四位数同时满足以下条件:① 是偶数;② ;③ ,请写出一个符合要求的数 .16. 如图,在平面直角坐标系 中,已知直线 ,直线 ,直线 交 于点 ,交 于点 ,过点 作y轴的垂线交 于点 ,过点 作x轴的垂线,交 于点 ,过点 作y轴的垂线交 于点 ,…,按此方式进行下去,则 的坐标为 , 的坐标为(用含n的式子表示,n为正整数). 17. 如下是小华设计的“作 的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).
17. 如下是小华设计的“作 的角平分线”的尺规作图过程,请帮助小华完成尺规作图并填空(保留作图痕迹).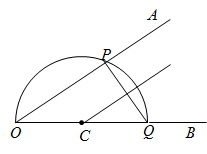
步骤
作法
推断
第一步
在 上任取一点C , 以点C为圆心, 为半径作半圆,分别交射线 于点P , 点Q , 连接
▲ ,理由是 ▲
第二步
过点C作 的垂线,交 于点D , 交 于点E
, ③
第三步
作射线
射线 平分
射线 为所求作.
三、解答题
-
18. 计算: .19. 解不等式: .20. 已知 ,求代数式 的值.21. 已知关于x的方程 有两个实数根.(1)、求k的取值范围;(2)、当k取最大整数时,求此时方程的根.22. 如图,在 中, , 为 的角平分线, ,连接 .
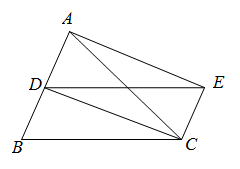 (1)、求证:四边形 为矩形:(2)、连接 ,若 ,求 的长.23. 在平面直角坐标系 中,直线 ,函数 的图象为F .(1)、若 在函数 的图象F上,求直线l对应的函数解析式:(2)、横、纵坐标都是整数的点叫做整点.记直线 ,图象F和直线 围成的区域(不含边界)为图形G .
(1)、求证:四边形 为矩形:(2)、连接 ,若 ,求 的长.23. 在平面直角坐标系 中,直线 ,函数 的图象为F .(1)、若 在函数 的图象F上,求直线l对应的函数解析式:(2)、横、纵坐标都是整数的点叫做整点.记直线 ,图象F和直线 围成的区域(不含边界)为图形G .①在(1)的条件下,写出图形G内的整点的坐标;
②若图形G内有三个整点,直接写出k的取值范围.
24. 某大学共有9000名学生,为了解该大学学生的阅读情况,小华设计调查问卷,用随机抽样的方式调查了150名学生,并对相关数据进行了收集、整理、描述和分析.下面是其中的部分信息:a . 所调查的150名学生最常用的一种阅读方式统计图如图1,
b . 选择手机阅读为最常用的一种阅读方式的学生中,平均每天阅读时长统计表如表1;
图1:最常用阅读方式统计图
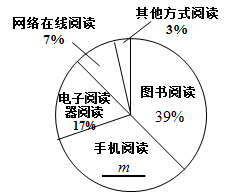
表1:使用手机阅读的学生平均每天阅读时长统计表
平均每天阅读时长x(单位:分钟)
人数
6
n
17
9
c . 使用手机阅读的学生中,平均每天阅读时长在 这一组的具体数据如下:60 60 66 68 68 69 70 70 2 72 72 73 75 80 83 84 85
根据以上信息解答下列问题:
(1)、图1中 , 表1中 ;(2)、使用手机阅读的学生中,平均天阅读时长的中位数是 , 平均每天阅读时长在 这一组的数据的众数是;(3)、根据所调查的这150名学生的阅读情况,估计该校使用手机阅读的学生中,平均每天阅读时长少于半小时的人数.25. 如图,在 中, ,点O在 上, ,点D在 上,以点O为圆心, 为半径作圆,交 的延长线于点E , 交 于点F , .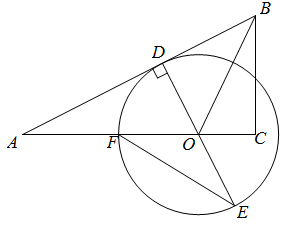 (1)、求证: 为⊙O的切线;(2)、若⊙O的半径为3, ,求 的长.26. 在平面直角坐标系 中, 为抛物线 上两点,其中 .(1)、求抛物线与x轴的交点坐标;(2)、若 ,点M , 点N在抛物线上运动,过点M作y轴的垂线,过点N作x轴的垂线,两条垂线交于点Q , 当 为等腰直角三角形时,求a的值;(3)、记抛物线在M , N两点之间的部分为图象G(包含M , N两点),若图象G上最高点与最低点的纵坐标之差为1,直接写出t的取值范围.27. 如图,在 中, ,点P为 外一点,点P与点C位于直线 异侧,且 ,过点C作 ,垂足为D .
(1)、求证: 为⊙O的切线;(2)、若⊙O的半径为3, ,求 的长.26. 在平面直角坐标系 中, 为抛物线 上两点,其中 .(1)、求抛物线与x轴的交点坐标;(2)、若 ,点M , 点N在抛物线上运动,过点M作y轴的垂线,过点N作x轴的垂线,两条垂线交于点Q , 当 为等腰直角三角形时,求a的值;(3)、记抛物线在M , N两点之间的部分为图象G(包含M , N两点),若图象G上最高点与最低点的纵坐标之差为1,直接写出t的取值范围.27. 如图,在 中, ,点P为 外一点,点P与点C位于直线 异侧,且 ,过点C作 ,垂足为D . (1)、当 时,在图1中补全图形,并直接写出线段 与 之间的数量关系;(2)、如图2,当 时,
(1)、当 时,在图1中补全图形,并直接写出线段 与 之间的数量关系;(2)、如图2,当 时,①用等式表示线段 与 之间的数量关系,并证明;
②在线段 上取一点K , 使得 ,画出图形并直接写出此时 的值.
28. 对于平面内的点M , 如果点P , 点Q与点M所构成的 是边长为1的等边三角形,则称点P , 点Q为点M的一对“关联点”,进一步地,在 中,若顶点M , P , Q按顺时针排列,则称点P , 点Q为点M的一对“顺关联点”;若顶点M , P , Q按逆时针排列,则称点P , 点Q为点M的一对“逆关联点”.已知 ,(1)、在 中,点A的一对关联点是 , 它们为点A的一对关联点(填“顺”或“逆”);(2)、以原点O为圆心作半径为1的圆,已知直线 .①若点P在⊙O上,点Q在直线l上,点P , 点Q为点A的一对关联点,求b的值;
②若在⊙O上存在点R , 在直线l上存在两点 和 ,其中 ,且点T , 点S为点R的一对顺关联点,求b的取值范围.