北京市门头沟区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 如图是某几何体的三视图,则该几何体是( )
 A、长方体 B、正方体 C、三棱柱 D、圆柱2. 在学习强国平台中,5月16日发布的“第一观察——天问落火”栏目的阅读量截止到5月17日中午,就已经达到了10895538人次,将10895538精确到万,得( )A、1089 B、1090 C、1089万 D、1090万3. 若代数式 值为零,则( )A、 B、 C、 D、4. 有一正方形卡纸,如图①,沿虚线向上翻折,得到图②,再沿虚线向右翻折得到图③,沿虚线将一角剪掉后展开,得到的图形是( )
A、长方体 B、正方体 C、三棱柱 D、圆柱2. 在学习强国平台中,5月16日发布的“第一观察——天问落火”栏目的阅读量截止到5月17日中午,就已经达到了10895538人次,将10895538精确到万,得( )A、1089 B、1090 C、1089万 D、1090万3. 若代数式 值为零,则( )A、 B、 C、 D、4. 有一正方形卡纸,如图①,沿虚线向上翻折,得到图②,再沿虚线向右翻折得到图③,沿虚线将一角剪掉后展开,得到的图形是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 方程组 的解为( )A、 B、 C、 D、6. 线段OA以点O为旋转中心,逆时针旋转60°,得到 ,再将 以点O为旋转中心逆时针旋转60°得到 ,依此操作直到点 与点A重合为止,顺次连接点A、 … 形成的多边形是( )A、正四边形 B、正五边形 C、正六边形 D、正七边形7. 如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
5. 方程组 的解为( )A、 B、 C、 D、6. 线段OA以点O为旋转中心,逆时针旋转60°,得到 ,再将 以点O为旋转中心逆时针旋转60°得到 ,依此操作直到点 与点A重合为止,顺次连接点A、 … 形成的多边形是( )A、正四边形 B、正五边形 C、正六边形 D、正七边形7. 如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )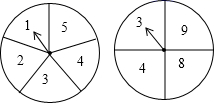 A、 B、 C、 D、8. 如图,是函数 (0≤x≤4)的图象,通过观察图象得出了如下结论:
A、 B、 C、 D、8. 如图,是函数 (0≤x≤4)的图象,通过观察图象得出了如下结论:⑴当x>3时,y随x的增大而增大;⑵该函数图象与x轴有三个交点;⑶该函数的最大值是6,最小值是﹣6;⑷当x > 0时,y随x的增大而增大.
以上结论中正确的有( )个
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. -3的倒数是。10. 已知 ,则x+y= .11. 比 大的整数中,最小的是 .12. 如图所示的正方形网格内,点A , B , C , D , E是网格线交点,那么 °.
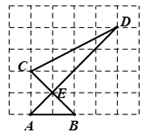 13. 如图,在△ABC中,D、E分别为AB、AC边的中点,若DE=2,则BC边的长为 .
13. 如图,在△ABC中,D、E分别为AB、AC边的中点,若DE=2,则BC边的长为 . 14. 若两圆的半径分别是1和3,且两圆的位置关系是相切,则圆心距为 .15. 一个函数满足过点 ,且当 时,y随x的增大而减小,该函数可以为 .16. 某单位设有6个部门,共153人,如下表:
14. 若两圆的半径分别是1和3,且两圆的位置关系是相切,则圆心距为 .15. 一个函数满足过点 ,且当 时,y随x的增大而减小,该函数可以为 .16. 某单位设有6个部门,共153人,如下表:部门
部门1
部门2
部门3
部门4
部门5
部门6
人数
25
16
23
32
43
14
参与了“学党史,名师德、促提升”建党100周年,“党史百题周周答活动”,一共十道题,每小题10分,满分100分;在某一周的前三天,由于特殊原因,有一个部门还没有参与答题,其余五个部门全部完成了答题,完成情况如下表:
分数
100
90
80
70
60
50及以下
比例
5
2
1
1
1
0
综上所述,未能及时参与答题的部门可能是 .
三、解答题
-
17. 计算: .18. 解分式方程: .19. 已知:如图, , ,请补充一个条件可以得到 .
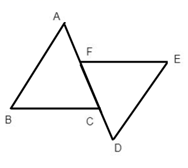
补充的条件: ▲ ;
证明:
20. 已知: ,求 的值.21. 已知,如图,直线l及直线外一点P.求作:过点P , 作直线l的平行线.

下面是一种方案的作法:
①在直线l上取一点A , 以点A为圆心,AP为半径作弧交直线于点B;
②分别以点B、点P为圆心,AP为半径作弧两弧交于点C;
③作直线PC;
直线PC为所求作的直线.
(1)、利用直尺和圆规依作法补全图形(保留作图痕迹);(2)、完成下面的证明.证明:连接PA、PC、BC
由①可得,PA=AB .
由②可得,PC=BC= PA .
∴ PC=BC= PA= AB ,
∴ , (填依据:)
∴ PC l .
22. 已如,如图,在△ABC中,AB=AC , AD是BC边的中线,过点A作BC的平行线,过点B作AD的平行线,两线交于点E , 连接DE交AB于点O .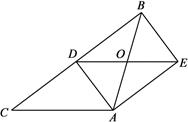 (1)、求证:四边形ADBE是矩形;(2)、若BC=8,AO= ,求四边形AEBC的面积.23. 在平面直角坐标系xOy中,反比例函数 的图象过点 .
(1)、求证:四边形ADBE是矩形;(2)、若BC=8,AO= ,求四边形AEBC的面积.23. 在平面直角坐标系xOy中,反比例函数 的图象过点 . (1)、求 的值;(2)、一次函数 与y轴相交于点M , 与反比例函数 ( )的图象交于点N , 过点 作x轴的平行线,过点 作y轴的平行线,两平行线相交于点Q , 当 时,通过画图,直接写出a的取值范围.24. 已知,如图,在△ 中, 是 边上一点,⊙ 过 三点,直线 是⊙ 的切线, .
(1)、求 的值;(2)、一次函数 与y轴相交于点M , 与反比例函数 ( )的图象交于点N , 过点 作x轴的平行线,过点 作y轴的平行线,两平行线相交于点Q , 当 时,通过画图,直接写出a的取值范围.24. 已知,如图,在△ 中, 是 边上一点,⊙ 过 三点,直线 是⊙ 的切线, .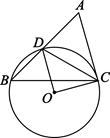 (1)、求 的度数;(2)、如果 ,⊙ 的半径为 ,求 的长.25. 2021年是中国共产党建党100周年,为了让学生了解更多的党史知识,某中学举行了一次“党史知识竞赛”,为了了解本次竞赛情况,从中抽取了初一、初二两个年级各50名学生,对他们此次竞赛的成绩(得分取正整数,满分为100分)分别进行了整理、描述和分析.下面给出部分信息.
(1)、求 的度数;(2)、如果 ,⊙ 的半径为 ,求 的长.25. 2021年是中国共产党建党100周年,为了让学生了解更多的党史知识,某中学举行了一次“党史知识竞赛”,为了了解本次竞赛情况,从中抽取了初一、初二两个年级各50名学生,对他们此次竞赛的成绩(得分取正整数,满分为100分)分别进行了整理、描述和分析.下面给出部分信息.a . 初一年级学生竞赛成绩的频数分布直方图如下 (数据分成6组:40≤x<50,50≤x<60,60≤x<70,70≤x<80,80≤x<90,90≤x<100):
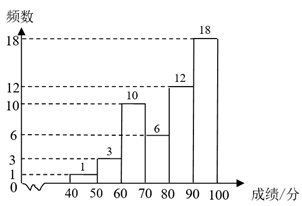
b . 初一年级学生竞赛成绩在80≤x<90这一组的是:
80 81 81 82 82 84 86 86 86 88 88 89
c . 这两个年级学生竞赛成绩的平均数、众数、中位数如下:
成绩
平均数
中位数
众数
初一年级学生
82
m
86
初二年级学生
83
85
84
根据以上信息,回答下列问题:
(1)、写出表中m的值;(2)、在此次竞赛中,竞赛成绩更好的是(填“初一”或“初二”),理由是 .(3)、已知该校初一年级有学生400人,估计该校初一年级学生竞赛成绩超过85的人数.26. 在平面直角坐标系xOy中,抛物线 的对称轴为直线x =2. (1)、求b的值;(2)、在y轴上有一动点P(0, ),过点P作垂直y轴的直线交抛物线于点 A(x1 , y1),B(x2 , y2),其中 .
(1)、求b的值;(2)、在y轴上有一动点P(0, ),过点P作垂直y轴的直线交抛物线于点 A(x1 , y1),B(x2 , y2),其中 .①当 时,结合函数图象,求出n的值;
②把直线PB上方的函数图象,沿直线PB向上翻折,图象的其余部分保持不变,得到一个新的图象W , 新图象W在0≤x≤5时,满足 ,求 的取值范围.
27. 已知,如图,∠MAN=90°,点B是∠MAN的内一点,且到AM , AN的距离相等.过点B做射线BC交AM于点C , 将射线BC绕点B逆时针旋转90°交AN于点D . (1)、依题意补全图形;(2)、求证:BC=BD;(3)、连接AB , 用等式表示线段AB , AC , AD之间的数量关系,并证明.28. 在△ABC中,点P是∠BAC的角平分线AD上的一点,若以点P为圆心,PA为半径的⊙P与△ABC的交点不少于4个,点P称为△ABC 关于∠BAC的“劲度点”,线段 PA的长度称为△ABC 关于∠BAC的“劲度距离”.(1)、如图,在∠BAC平分线AD上的四个点 、 、 、 中,连接点A和点的线段长度是△ABC关于∠BAC的“劲度距离”.
(1)、依题意补全图形;(2)、求证:BC=BD;(3)、连接AB , 用等式表示线段AB , AC , AD之间的数量关系,并证明.28. 在△ABC中,点P是∠BAC的角平分线AD上的一点,若以点P为圆心,PA为半径的⊙P与△ABC的交点不少于4个,点P称为△ABC 关于∠BAC的“劲度点”,线段 PA的长度称为△ABC 关于∠BAC的“劲度距离”.(1)、如图,在∠BAC平分线AD上的四个点 、 、 、 中,连接点A和点的线段长度是△ABC关于∠BAC的“劲度距离”. (2)、在平面直角坐标系中,已知点M(0,t),N (4,0).
(2)、在平面直角坐标系中,已知点M(0,t),N (4,0).①当t= 时,求出△MON 关于∠MON的“劲度距离” 的最大值.
②如果 内至少有一个值是△MON 关于∠MON的“劲度距离”,请直接写出t的取值范围.
