北京市海淀区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 下列图形中,是圆锥侧面展开图的是( )A、三角形 B、圆 C、扇形 D、矩形2. 如图,点A是数轴上一点,点A , B表示的数互为相反数,则点B表示的数可能是( )
 A、0 B、1 C、1.5 D、2.53. 如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )
A、0 B、1 C、1.5 D、2.53. 如图,将一个正方形纸片沿图中虚线剪开,能拼成下列四个图形,其中是中心对称图形的是( )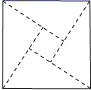 A、
A、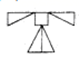 B、
B、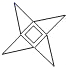 C、
C、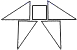 D、
D、 4. 下列运算正确的是( )A、 B、 C、 D、5. 反比例函数 (k为正整数)在第一象限的图象如图所示,已知图中点A的坐标为 ,则k的值是( )
4. 下列运算正确的是( )A、 B、 C、 D、5. 反比例函数 (k为正整数)在第一象限的图象如图所示,已知图中点A的坐标为 ,则k的值是( ) A、1 B、2 C、3 D、46. 如图,AB是 的直径,PA与 相切于点A , 交 于点C . 若 ,则 的度数为( )
A、1 B、2 C、3 D、46. 如图,AB是 的直径,PA与 相切于点A , 交 于点C . 若 ,则 的度数为( ) A、 B、 C、 D、7. 某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),数据分成6组: , , , , ,如图是根据数据绘制的统计图.下列说法正确的是( )
A、 B、 C、 D、7. 某餐厅规定等位时间达到30分钟(包括30分钟)可享受优惠.现统计了某时段顾客的等位时间t(分钟),数据分成6组: , , , , ,如图是根据数据绘制的统计图.下列说法正确的是( )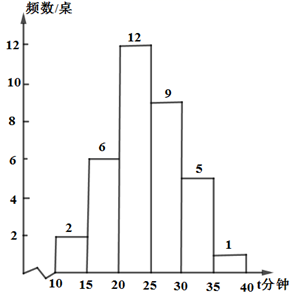 A、此时段有1桌顾客等位时间是40分钟 B、此时段平均等位时间小于20分钟 C、此时段等位时间的中位数可能是27 D、此时段有6桌顾客可享受优惠8. 如图,一架梯子AB靠墙而立,梯子顶端B到地面的距离BC为 ,梯子中点处有一个标记,在梯子顶端B竖直下滑的过程中,该标记到地面的距离y与顶端下滑的距离x满足的函数关系是( )
A、此时段有1桌顾客等位时间是40分钟 B、此时段平均等位时间小于20分钟 C、此时段等位时间的中位数可能是27 D、此时段有6桌顾客可享受优惠8. 如图,一架梯子AB靠墙而立,梯子顶端B到地面的距离BC为 ,梯子中点处有一个标记,在梯子顶端B竖直下滑的过程中,该标记到地面的距离y与顶端下滑的距离x满足的函数关系是( ) A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系
A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系二、填空题
-
9. 若代数式 有意义,则实数x的取值范围是 .10. 分解因式:11. 比较大小: 3(填“˃”或“=”或“<”).12. 盒中有1枚白色棋子和1枚黑色棋子,这两枚棋子除颜色外无其他差别,从中随机摸出一枚棋子,记录其颜色,放回后,再从中随机摸出一枚棋子,记录其颜色,那么两次记录的颜色都是黑色的概率是 .13. 如图,两条射线 ,点C , D分别在射线BN , AM上,只需添加一个条件,即可证明四边形ABCD是平行四边形,这个条件可以是(写出一个即可).
 14. 《孙子算经》是中国南北朝时期重要的数学专著,其中包含了“鸡兔同笼”“物不知数”等许多有趣的数学问题.《孙子算经》中记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其译文为:“用一根绳子去量一根长木,绳子还剩余4.5尺.将绳子对折再量长木,长木还剩余1尺,问木长多少尺?”设木长x尺,绳子长y尺,可列方程组为 .15. 如图所示的网格是正方形网格,A , B , C , D是网格线交点,则 与 的大小关系为: (填“>”,“=”或“<”).
14. 《孙子算经》是中国南北朝时期重要的数学专著,其中包含了“鸡兔同笼”“物不知数”等许多有趣的数学问题.《孙子算经》中记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”其译文为:“用一根绳子去量一根长木,绳子还剩余4.5尺.将绳子对折再量长木,长木还剩余1尺,问木长多少尺?”设木长x尺,绳子长y尺,可列方程组为 .15. 如图所示的网格是正方形网格,A , B , C , D是网格线交点,则 与 的大小关系为: (填“>”,“=”或“<”). 16. 小云计划户外徒步锻炼,每天有“低强度”“高强度”“休息”三种方案,下表对应了每天不同方案的徒步距离(单位: ).若选择“高强度”要求前一天必须“休息”(第一天可选择“高强度”).则小云5天户外徒步锻炼的最远距离为 .
16. 小云计划户外徒步锻炼,每天有“低强度”“高强度”“休息”三种方案,下表对应了每天不同方案的徒步距离(单位: ).若选择“高强度”要求前一天必须“休息”(第一天可选择“高强度”).则小云5天户外徒步锻炼的最远距离为 .日期
第1天
第2天
第3天
第4天
第5天
低强度
8
6
6
5
4
高强度
12
13
15
12
8
休息
0
0
0
0
0
三、解答题
-
17. 计算: .18. 解方程: .19. 先化简再求值: ,其中 .20. 已知: ,B为射线AN上一点.
求作: ,使得点C在射线AM上,且 .

作法:①以点A为圆心,AB长为半径画弧,交射线AM于点D , 交射线AN的反向延长线于点E;
②以点E为圆心,BD长为半径画弧,交 于点F;
③连接FB , 交射线AM于点C .
就是所求作的三角形.
(1)、使用直尺和圆规,依作法补全图形(保留作图痕迹); (2)、完成下面的证明:
(2)、完成下面的证明:证明:连接BD , EF , AF ,
∵点B , E , F在 上,
()(填写推理的依据).
∵在 中, ,
.
.
21. 关于x的一元二次方程 .(1)、求证:方程总有两个实数根;(2)、若方程有一个根小于1,求m的取值范围.22. 如图1, 中,D为AC边上一动点(不含端点),过点D作 交BC于点E , 过点E作 交AB于点F , 连接AE , DF . 点D运动过程中,始终有 . (1)、求证: ;(2)、如图2,若 ,当 时,求AD的长.23. 平面直角坐标系 中,一次函数 的图象经过点 .(1)、求这个一次函数的解析式;(2)、当 时,对于x的每一个值,函数 的值都大于一次函数 的值,直接写出a的取值范围.24. 如图,AB为 的直径,点C在AB的延长线上,CD与 相切于D , 过点B作 交 于点E , 连接AD , AE .
(1)、求证: ;(2)、如图2,若 ,当 时,求AD的长.23. 平面直角坐标系 中,一次函数 的图象经过点 .(1)、求这个一次函数的解析式;(2)、当 时,对于x的每一个值,函数 的值都大于一次函数 的值,直接写出a的取值范围.24. 如图,AB为 的直径,点C在AB的延长线上,CD与 相切于D , 过点B作 交 于点E , 连接AD , AE . (1)、求 的度数;(2)、若 ,求BE的长.25. 品味诗词之美,传承中华文明,央视节目《中国诗词大会》备受大众欢迎.节目规则如下:由100位诗词爱好者组成的百人团与挑战者共同答题,每位挑战者最多可答五轮题.每轮比赛答题时,如挑战者答对,则百人团答错的人数即为选手该轮得分;如挑战者答错,则该轮不得分,且停止答题.每轮比赛的得分之和即为挑战者的总得分.现有甲、乙、丙三人作为挑战者参加节目答题,相关信息如下:
(1)、求 的度数;(2)、若 ,求BE的长.25. 品味诗词之美,传承中华文明,央视节目《中国诗词大会》备受大众欢迎.节目规则如下:由100位诗词爱好者组成的百人团与挑战者共同答题,每位挑战者最多可答五轮题.每轮比赛答题时,如挑战者答对,则百人团答错的人数即为选手该轮得分;如挑战者答错,则该轮不得分,且停止答题.每轮比赛的得分之和即为挑战者的总得分.现有甲、乙、丙三人作为挑战者参加节目答题,相关信息如下:a . 甲、乙两人参加比赛的得分统计图如下,每个点的横坐标与纵坐标分别表示甲、乙二人在相同轮次的得分:

b . 丙参加比赛的得分统计图如下:

根据以上信息,回答下列问题:
(1)、已知点A的坐标为 ,则此轮比赛中:甲的得分为 , 与甲同场答题的百人团中,有人答对;(2)、这五轮比赛中,甲得分高于乙得分的比赛共有轮;甲、乙、丙三人中总得分最高的为;(3)、设甲参加的第一轮至第五轮比赛时百人团答对人数的方差为 ,乙参加的第一轮至第五轮比赛时百人团答对人数的方差为 ,则 (填“>”,“<”或“=”).26. 在平面直角坐标系 中,抛物线 与y轴的交点为A , 过点A作直线l垂直于y轴.(1)、求抛物线的对称轴(用含m的式子表示);(2)、将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G . 点 , 图形G上任意两点.①当 时,若 ,判断 与 的大小关系,并说明理由;
②若对于 ,都有 ,求m的取值范围.
27. 已知 ,点A在边OM上,点P是边ON上一动点, ,将线段AP绕点A逆时针旋转 ,得到线段AB , 连接OB , 再将线段OB绕点O顺时针旋转 ,得到线段OC , 作 于点H . (1)、如图1, .
(1)、如图1, .①依题意补全图形;
②连接BP , 求 的度数;
(2)、如图2,当点P在射线ON上运动时,用等式表示线段OA与CH之间的数量关系,并证明.28. 在平面直角坐标系 中, 是k个互不相同的点,若这k个点横坐标的不同取值有m个,纵坐标的不同取值有n个, ,则称p为这k个点的“特征值”,记为 .如图1,点 . (1)、如图2,圆C的圆心为 ,半径为5,与x轴交于A , B两点.
(1)、如图2,圆C的圆心为 ,半径为5,与x轴交于A , B两点.① ▲ , ▲ ;
②直线 与圆C交于两点D , E , 若 ,求b的取值范围;
(2)、点 到点O的距离为1或 ,且这8个点构成中心对称图形, ,若抛物线 恰好经过 中的三个点,并以其中一个点为顶点,直接写出a的所有可能取值.