北京市丰台区2021年中考数学二模试卷

试卷更新日期：2021-06-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图是某几何体的三视图，该几何体是（）

A、圆锥 B、圆柱 C、三棱柱 D、长方体

查看试题解析
2. $2020$ 年 $12$ 月 $17$ 日凌晨，嫦娥 $5$ 号返回器携带月球样本成功着陆．已知地球到月球的平均距离约为 $380000$ 千米．将 $380000$ 用科学记数法表示为（）

A、 $3.8 \times 10^{5}$ B、 $3.8 \times 10^{6}$ C、 $38 \times 10^{4}$ D、 $0.38 \times 10^{6}$

查看试题解析
3. 下列交通标志中，是中心对称图形的是（）

A、禁止驶入 B、靠左侧道路行驶 C、向左和向右转弯 D、环岛行驶

查看试题解析
4. 若 $a > b$ ，则下列不等式一定成立的是（）

A、 $a - 3 < b - 3$ B、 $- 2 a < - 2 b$ C、 $\frac{a}{4} < \frac{b}{4}$ D、 $a^{2} < b^{2}$

查看试题解析
5. 下列计算正确的是（）

A、 $a^{2} + a^{3} = a^{5}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(2 a)}^{3} = 6 a^{3}$ D、 ${(a^{2})}^{3} = a^{6}$

查看试题解析
6. 如图，l₁∥l₂ ，点O在直线l₁上，将三角板的直角顶点放在点O处，三角板的两条直角边与l₂交于A ， B两点，若∠1＝35°，则∠2的度数为（）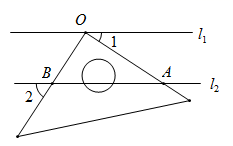

A、35° B、45° C、55° D、65°

查看试题解析
7. 学校要举行运动会，小亮和小刚报名参加100米短跑项目的比赛，预赛分A ， B ， C三组进行，小亮和小刚恰好在同一个组的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
8. 某公司新产品上市30天全部售完．图1表示产品的市场日销售量与上市时间之间的关系，图2表示单件产品的销售利润与上市时间之间的关系，下列四个结论中错误的是（）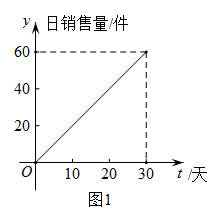

A、第30天该产品的市场日销售量最大 B、第20天至30天该产品的单件产品的销售利润最大 C、第20天该产品的日销售总利润最大 D、第20天至30天该产品的日销售总利润逐日增多

查看试题解析

二、填空题

9. 若 $\sqrt{x + 1}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
10. 若一个多边形的内角和是 $540^{°}$ ，则该多边形的边数是.

查看试题解析
11. 写出一个比2大且比3小的无理数：．

查看试题解析
12. 如图，⊙O是△ABC的外接圆，半径是2，∠BAC＝60°，则 $\overset{⌢}{B C}$ 的长是．

查看试题解析
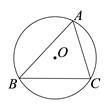13. 如图所示的网格是正方形网格，A ， B ， C ， D 是网格线交点，则△ABC与△DBC面积的大小关系为：S_△ABC S_△DBC（填“＞”，“＝”或“＜”）．

查看试题解析
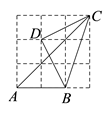14. 随着5G网络技术的发展，市场对5G产品的需求越来越大．为满足市场需求，某大型5G产品生产厂家更新技术后，加快了生产速度．现在平均每天比更新技术前多生产30万件产品，现在生产500万件产品所需的时间与更新技术前生产400万件产品所需时间相同．设更新技术前每天生产x万件，依据题意列出关于x的方程．

查看试题解析
15. 已知抛物线 $y = x^{2} - (m + 1) x$ 与 $x$ 轴的一个交点的横坐标大于1且小于2，则m的取值范围是．

查看试题解析
16. 某单位有10000名职工，想通过验血的方式筛查出某种病毒的携带者．如果对每个人的血样逐一化验，需要化验10000次．统计专家提出了一种化验方法：随机地按5人一组分组，然后将各组5个人的血样混合再化验．如果混合血样呈阴性，说明这5个人全部阴性；如果混合血样呈阳性，说明其中至少有一个人呈阳性，就需要对这组的每个人再分别化验一次．假设携带该病毒的人数占0.05%．回答下列问题：

(1)、按照这种化验方法是否能减少化验次数（填“是”或“否”）；

(2)、按照这种化验方法至多需要次化验，就能筛查出这10000名职工中该种病毒的携带者．

查看试题解析

三、解答题

17. 计算： $\sqrt{8} + {(\frac{1}{3})}^{- 1} - 2021^{0} - 2 \cos 45 °$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} 2 x + 3 \leq x + 6 \\ \frac{2 x + 5}{3} > x - 1 \end{array}$

查看试题解析
19. 如图，AB＝AD ， AC＝AE ， ∠BAE＝∠DAC ．求证：∠C＝∠E ．

查看试题解析
20. 已知 $x = 2 y$ ，求代数式 $(\frac{1}{y} - \frac{1}{x}) \div \frac{x^{2} - 2 x y + y^{2}}{x^{2} y}$ 的值．

查看试题解析
21. 下面是小融设计的“过直线外一点作圆与这条直线相切”的尺规作图过程．
已知：直线 $l$ 及直线 $l$ 外一点P（如图1）．

求作：⊙P ，使它与直线 $l$ 相切．

作法：如图2，

①在直线 $l$ 上任取两点A ， B；

②分别以点A ，点B为圆心，AP ， BP的长为半径画弧，两弧交于点Q；

③作直线PQ ，交直线 $l$ 于点C；

④以点P为圆心，PC的长为半径画⊙P ．

所以⊙P即为所求．

根据小融设计的尺规作图过程，

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明．
证明：连接AP ， AQ ， BP ， BQ ．

∵AP＝▲，BP＝▲，

∴点A ，点B在线段PQ的垂直平分线上．

∴直线AB是线段PQ的垂直平分线．

∵PQ⊥ $l$ ，PC是⊙P的半径，

∴⊙P与直线 $l$ 相切（）（填推理的依据）．

查看试题解析
22. 如图，在△ABC中，∠BAC＝90°，AD是BC边上的中线，AE∥BC ， CE∥AD ．

(1)、求证：四边形ADCE是菱形；

(2)、连接BE ，若∠ABC＝30°，AC＝2，求BE的长．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，直线 $y = k x + b (k \neq 0)$ 与反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象交于点 $A (- 1 ， n)$ ， $B (2 ， - 1)$ 两点．

(1)、求 $m ， n$ 的值；

(2)、已知点 $P (a ， 0) (a > 0)$ ，过点 $P$ 作 $x$ 轴的垂线，分别交直线 $y = k x + b (k \neq 0)$ 和反比例函数 $y = \frac{m}{x} (m \neq 0)$ 的图象于点 $M ， N$ ，若线段 $M N$ 的长随 $a$ 的增大而增大，直接写出 $a$ 的取值范围．

查看试题解析
24. 如图，⊙O是△ABC的外接圆，AB是直径，D是AC中点，过点A作⊙O的切线交直线OD于点P ，连接PC ．

(1)、求证：∠PCA＝∠ABC；

(2)、若BC＝4，tan∠APO＝ $\frac{1}{2}$ ，求PA的长．

查看试题解析

25. 2021年7月1日是中国共产党成立100周年纪念日．为了让全校学生牢固树立爱国爱党的崇高信念，某校开展了形式多样的党史学习教育活动．八、九年级各300名学生举行了一次党史知识竞赛后随机抽取了八、九年级各20名学生的成绩进行了整理与分析，部分信息如下：

a ．抽取九年级20名学生的成绩如下：

86	88	97	91	94	62	51	94	87	71
94	78	92	55	97	92	94	94	85	98

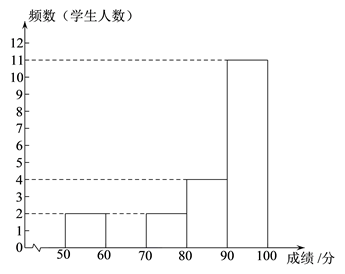
b ．抽取九年级20名学生的成绩频数分布直方图如下（数据分成5组： $50 \leq x < 60$ ， $60 \leq x < 70$ ， $70 \leq x < 80$ ， $80 \leq x < 90$ ， $90 \leq x \leq 100$ ）：

c ．九年级抽取的20名学生成绩的平均数、中位数、方差如下表：

年级	平均数	中位数	方差
九年级	85	m	192

请根据以上信息，回答下列问题：

(1)、补全频数分布直方图，写出表中m的值；

(2)、若90分及以上为优秀，估计此次知识竞赛中九年级成绩优秀的学生人数；

(3)、通过分析随机抽取的八年级20名学生的成绩发现：这20名学生成绩的中位数为88，方差为80.4，且八、九两个年级随机抽取的共40名学生成绩的平均数是85.2

①求八年级这20名学生成绩的平均数；

②你认为哪个年级的成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．

查看试题解析

26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = a x^{2} + b x + a - 5 (a \neq 0)$ 的对称轴是直线 $x = 1$ ．

(1)、用含 $a$ 的式子表示 $b$ ；

(2)、求抛物线的顶点坐标；

(3)、若抛物线与 $y$ 轴的一个交点为 $A (0 ， - 4)$ ，且当 $m \leq x \leq n$ 时， $y$ 的取值范围是 $- 5 \leq y \leq n$ ，结合函数图象，直接写出一个满足条件的 $n$ 的值和对应 $m$ 的取值范围．

查看试题解析
27. 已知∠MON＝90°，点A ， B分别在射线OM ， ON上（不与点O重合），且OA＞OB ， OP平分∠MON ，线段AB的垂直平分线分别与OP ， AB ， OM交于点C ， D ， E ，连接CB ，在射线ON上取点F ，使得OF＝OA ，连接CF ．

(1)、依题意补全图形；

(2)、求证：CB＝CF；

(3)、用等式表示线段CF与AB之间的数量关系，并证明．

查看试题解析
28. 对于平面内点P和⊙G ，给出如下定义：T是⊙G上任意一点，点P绕点T旋转180°后得到点P＇，则称点P＇为点P关于⊙G的旋转点．下图为点P及其关于⊙G的旋转点P＇的示意图．在平面直角坐标系xOy中，⊙O的半径为1，点P（0，－2）．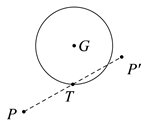

(1)、在点A（－1，0），B（0，4），C（2，2）中，是点P关于⊙O的旋转点的是；

(2)、若在直线 $y = x + b$ 上存在点P关于⊙O的旋转点，求 $b$ 的取值范围；

(3)、若点D在⊙O上，⊙D的半径为1，点P关于⊙D的旋转点为点P＇，请直接写出点P＇的横坐标 $x$ _P_＇的取值范围．

查看试题解析