北京市东城区2021年中考数学二模试卷

试卷更新日期：2021-06-11 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列各数中，小于 $\sqrt{2}$ 的正整数是（）

A、-1 B、0 C、1 D、2

查看试题解析
2. 在下列不等式中，解集为 $x > - 1$ 的是（）

A、 $2 x > 2$ B、 $- 2 x > - 2$ C、 $2 x < - 2$ D、 $- 2 x < 2$

查看试题解析
3. 在平面直角坐标系 $x O y$ 中，⊙O的半径为2，点A（1， $\sqrt{3}$ ）与⊙O的位置关系是（）

A、在⊙O上 B、在⊙O内 C、在⊙O外 D、不能确定

查看试题解析
4. 下列式子中，运算正确的是（）

A、 ${(1 + x)}^{2} = 1 + x^{2}$ B、 $a^{2} \cdot a^{4} = a^{8}$ C、 $- (x - y) = - x - y$ D、 $a^{2} + 2 a^{2} = 3 a^{2}$

查看试题解析
5. 如图，⊙O是正五边形ABCDE的外接圆．若⊙O的半径为5，则半径OA ， OB与 $\overset{⌢}{A B}$ 围成的扇形的面积是（）

A、 $2 π$ B、 $5π$ C、 $\frac{25}{6} π$ D、 $10π$

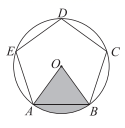查看试题解析
6. 在平面直角坐标系 $x O y$ 中，点A，B是直线 $y = x$ 与双曲线 $y = \frac{4}{x}$ 的交点，点B在第一象限，点C的坐标为（6，-2）．若直线BC交x轴于点D ，则点D的横坐标为（）

A、2 B、3 C、4 D、5

查看试题解析
7. 多年来，北京市以强有力的措施和力度治理大气污染，空气质量持续改善，主要污染物的年平均浓度值全面下降．下图是1998年至2019年二氧化硫（SO₂）和二氧化氮（NO₂）的年平均浓度值变化趋势图．下列说法错误的是（）

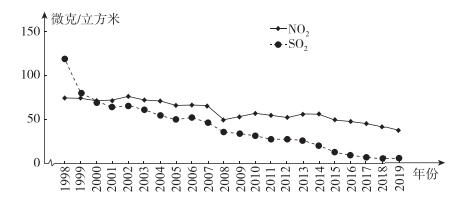A、1998年至2019年，SO₂的年平均浓度值的平均数小于NO₂的年平均浓度值的平均数 B、1998年至2019年，SO₂的年平均浓度值的中位数小于NO₂的年平均浓度值的中位数 C、1998年至2019年，SO₂的年平均浓度值的方差小于NO₂的年平均浓度值的方差 D、1998年至2019年，SO₂的年平均浓度值比NO₂的年平均浓度值下降得更快

查看试题解析
8. 四位同学在研究函数y=-x²+bx+c（b ， c是常数）时，甲同学发现当x=1时，函数有最大值；乙同学发现函数y=-x²+bx+c的图象与y轴的交点为（0，-3）；丙同学发现函数的最大值为4；丁同学发现当x=3时，函数的值为0．若这四位同学中只有一位同学的结论是错误的，则该同学是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题

9. 要使分式 $\frac{2}{x - 1}$ 有意义，则x的取值范围是．

查看试题解析
10. 分解因式： $m x^{2} - 9 m =$ ．

查看试题解析
11. 用一个 $k$ 的值推断命题“一次函数 $y = k x + 1 (k \neq 0)$ 中， $y$ 随着 $x$ 的增大而增大．”是错误的，这个值可以是 $k$ = ．

查看试题解析
12. 某校九年级（1）班计划开展“讲中国好故事”主题活动．第一小组的同学推荐了“北大红楼、脱贫攻坚、全面小康、南湖红船、抗疫精神、致敬英雄”六个主题，并将这六个主题分别写在六张完全相同的卡片上，然后将卡片放入不透明的口袋中．组长小东从口袋中随机抽取一张卡片，抽到含“红”字的主题卡片的概率是．

查看试题解析
13. 如图，点A，D，B，E在同一条直线上，AD=BE ， AC=EF ，要使△ABC≌△EDF ，只需添加一个条件，这个条件可以是．

查看试题解析
14. 在平面直角坐标系xOy中，已知点A(2，0)，B(5，4)．若四边形OABC是平行四边形，则平行四边形OABC的周长等于．

查看试题解析
15. 若点P在函数 $y = {\begin{array}{l} x ， x \geq 0 \\ - x ， x < 0 \end{array}$ 的图象上，且到x轴的距离等于1，则点P的坐标是．

查看试题解析
16. 数学课上，李老师提出如下问题：
已知：如图， $A B$ 是⊙O的直径，射线 $A C$ 交⊙O于 $C$ ．

求作：弧 $B C$ 的中点D ．

同学们分享了如下四种方案：

①如图1，连接BC ，作BC的垂直平分线，交⊙O于点D ．

②如图2，过点O作AC的平行线，交⊙O于点D ．

③如图3，作∠BAC的平分线，交⊙O于点D ．

④如图4，在射线AC上截取AE ，使AE=AB ，连接BE ，交⊙O于点D ．

上述四种方案中，正确的方案的序号是．

查看试题解析

三、解答题

17. 计算： ${(- 5)}^{0} + \sqrt{27} {+2}^{- 1} - \tan 60 °$

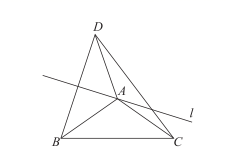
查看试题解析
18. 先化简代数式 $\frac{a^{2} + 1}{a - 1} + 1 - a$ ，再求当 $a$ 满足 $a - 2 = 0$ 时，此代数式的值．

查看试题解析
19. 如图，在等腰△ABC中，AB=AC ，直线l过点A．点B与点D关于直线l对称，连接AD ， CD ．求证：∠ACD=∠ADC ．

查看试题解析
20. 已知：如图，点C在∠MON的边OM上．
求作：射线CD ，使CD $//$ ON ，且点D在∠MON的角平分线上．

作法：①以点O为圆心，适当长为半径画弧，分别交射线OM ， ON于点A ， B；

②分别以点A ， B为圆心，大于 $\frac{1}{2} A B$ 的长为半径画弧，交于点Q；

③画射线OQ；

④以点C为圆心，CO长为半径画弧，交射线OQ于点D；

⑤画射线CD ．

射线CD就是所求作的射线．

(1)、使用直尺和圆规，依作法补全图形（保留作图痕迹）；

(2)、完成下面的证明：
∵OD平分∠MON ，

∴∠MOD=   ▲   ．

∵OC=CD ，

∴∠MOD=   ▲   ．

∴∠NOD=∠CDO ．

∴CD $//$ ON（       ▲        ）（填推理的依据）．

查看试题解析
21. 已知关于 $x$ 的一元二次方程 $m x^{2} - (m + 1) x + 1 = 0 (m \neq 0)$ ．

(1)、求证：此方程总有实数根；

(2)、写出一个 $m$ 的值，使得此该方程的一个实数根大于1，并求此时方程的根．

查看试题解析
22. 如图，在菱形ABCD中，点E是CD的中点，连接AE ，交BD于点F ．

(1)、求BF：DF的值；

(2)、若AB=2，AE= $\sqrt{3}$ ，求BD的长．

查看试题解析
23. 在平面直角坐标系xOy中，直线l与双曲线 $y = \frac{k}{x} (k \neq 0)$ 的两个交点分别为A（-3，-1），B（1，m）．

(1)、求k和m的值；

(2)、点P为直线l上的动点，过点P作平行于x轴的直线，交双曲线 $y = \frac{k}{x} (k \neq 0)$ 于点Q．当点Q位于点P的右侧时，求点P的纵坐标n的取值范围．

查看试题解析
24. 如图，⊙O是△ABC的外接圆，圆心O在AC上．过点B作直线交AC的延长线于点D ，使得∠CBD=∠CAB ．过点A作AE⊥BD于点E ，交⊙O于点F ．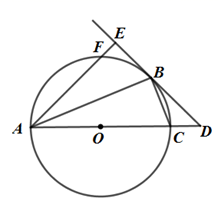

(1)、求证：BD是⊙O的切线；

(2)、若AF=4， $\sin D = \frac{2}{3}$ ，求BE的长．

查看试题解析
25. 中国新闻出版研究院组织实施的全国国民阅读调查已持续开展了18次，对我国国民阅读总体情况进行了综合分析.2021年4月23日，第十八次全国国民阅读调查结果发布．
下面是关于样本及国民图书阅读量的部分统计信息．

a ．本次调查有效样本容量为46083，成年人和未成年人样本容量的占比情况如图1．

b.2020年，成年人的人均纸质图书阅读量约为4.70本，人均电子书阅读量约为3.29本；2019年，成年人的人均纸质图书阅读量约为4.65本，人均电子书阅读量约为2.84本．

c.2012年至2020年，未成年人的年人均图书阅读量如图2．

根据以上信息，回答问题：

(1)、第十八次全国国民阅读调查中，未成年人样本容量占有效样本容量的；

(2)、2020年，成年人的人均图书阅读量约为本，比2019年多本；

(3)、在2012年至2020年中后一年与前一年相比，年未成年人的年人均图书阅读量的增长率最大；

(4)、2020年，未成年人的人均图书阅读量比成年人的人均图书阅读量高%（结果保留整数）．

查看试题解析
26. 在平面直角坐标系xOy中，抛物线 $y = a x^{2} - 3 a x + 1$ 与y轴交于点A ．

(1)、求抛物线的对称轴；

(2)、点B是点A关于对称轴的对称点，求点B的坐标；

(3)、已知点P(0，2)，Q $(a + 1 ， 1)$ ，若线段PQ与抛物线与恰有一个公共点，结合函数图象，求a的取值范围．

查看试题解析
27. 已知△ADE和△ABC都是等腰直角三角形，∠ADE=∠BAC=90°，P为AE的中点，连接DP ．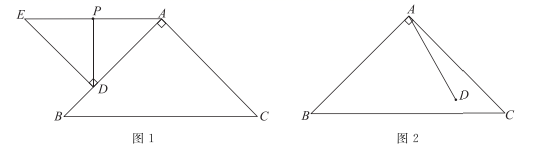

(1)、如图1，点A ， B ， D在同一条直线上，直接写出DP与AE的位置关系；

(2)、将图1中的△ADE绕点A逆时针旋转，当AD落在图2所示的位置时，点C ， D ， P恰好在同一条直线上．
①在图2中，按要求补全图形，并证明∠BAE=∠ACP；

②连接BD ，交AE于点F ．判断线段BF与DF的数量关系，并证明．

查看试题解析
28. 对于平面直角坐标系xOy中的图形W ，给出如下定义：点P是图形W上任意一点，若存在点Q ，使得∠OQP是直角，则称点Q是图形W的“直角点”．

(1)、已知点A $(6 ， 8)$ ，在点Q₁ $(0 ， 8)$ ，Q₂ $(- 4 ， 2)$ ，Q₃ $(8 ， 4)$ 中，是点A的“直角点”；

(2)、已知点 $B (- 3 ， 4)$ ， $C (4 ， 4)$ ，若点Q是线段BC的“直角点”，求点Q的横坐标 $n$ 的取值范围；

(3)、在（2）的条件下，已知点 $D (t ， 0)$ ， $E (t + 1 ， 0)$ ，以线段DE为边在x轴上方作正方形DEFG ．若正方形DEFG上的所有点均为线段BC的“直角点”，直接写出t的取值范围．

查看试题解析