北京市昌平区2021年中考数学二模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 自2021年1月1日起,全市启动九类重点人群新冠疫苗接种工作.昌平设置46个疫苗接种点位,共配备医务人员1200多名.截至3月28日18时,昌平区累计新冠疫苗接种共完成1015000人次,整体接种秩序井然.将1015000用科学记数法表示应为( )A、 B、 C、 D、2. 下列几何体的主视图和俯视图完全相同的是( )A、
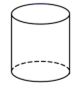 B、
B、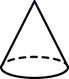 C、
C、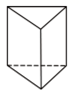 D、
D、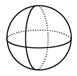 3. 下列图形中是轴对称图形,但不是中心对称图形的是( )A、
3. 下列图形中是轴对称图形,但不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 实数a , b , c , d在数轴上对应的点的位置如图所示,下列结论正确的是( )
4. 实数a , b , c , d在数轴上对应的点的位置如图所示,下列结论正确的是( ) A、|a|<|b| B、ad>0 C、a+c>0 D、d-a>05. 若一个多边形的内角和等于其外角和,则这个多边形的边数是( )A、3 B、4 C、5 D、66. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A , B , E在x轴上,若正方形BEFG的边长为12,则C点坐标为( )
A、|a|<|b| B、ad>0 C、a+c>0 D、d-a>05. 若一个多边形的内角和等于其外角和,则这个多边形的边数是( )A、3 B、4 C、5 D、66. 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A , B , E在x轴上,若正方形BEFG的边长为12,则C点坐标为( )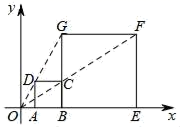 A、(6,4) B、(6,2) C、(4,4) D、(8,4)7. 疫情期间进入学校都要进入测温通道,体温正常才可进入学校,昌平某校有2个测温通道,分别记为A、B通道,学生可随机选取其中的一个通道测温进校园.某日早晨该校所有学生体温正常.小王和小李两同学该日早晨进校园时,选择同一通道测温进校园的概率是( )A、 B、 C、 D、8. 世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(°F)两种,它们之间的换算关系如下表所示:
A、(6,4) B、(6,2) C、(4,4) D、(8,4)7. 疫情期间进入学校都要进入测温通道,体温正常才可进入学校,昌平某校有2个测温通道,分别记为A、B通道,学生可随机选取其中的一个通道测温进校园.某日早晨该校所有学生体温正常.小王和小李两同学该日早晨进校园时,选择同一通道测温进校园的概率是( )A、 B、 C、 D、8. 世界各国温度的计量单位尚不统一,常用的有摄氏温度(℃)和华氏温度(°F)两种,它们之间的换算关系如下表所示:摄氏(单位℃)
…
0
1
2
3
4
5
6
…
华氏(单位°F)
…
32
33.8
35.6
37.4
39.2
41
42.8
…
那么当华氏度与摄氏度对应相等时的温度值是( )
A、32 B、-20 C、-40 D、40二、填空题
-
9. 代数式 有意义时,x应满足的条件是 .10. 将一副三角板如图摆放,斜边AB与直角边DE相交于点F , 则 .
 11. 写出一个比 小的正整数是 .12. 如图所示的网格是正方形网格,点A , B , C , D是网格线交点,则 的面积与 的面积大小关系为: (填“>”“=”或“<”),
11. 写出一个比 小的正整数是 .12. 如图所示的网格是正方形网格,点A , B , C , D是网格线交点,则 的面积与 的面积大小关系为: (填“>”“=”或“<”), 13. 方程组 的解为 .14. 今年五月某中学举行一次“新冠”防疫知识竞赛,该校九年级1班、2班各选派了6名学生参赛,为了全面了解、比较两个班级的参赛学生的实力,请你根据下表成绩对他们进行统计分析:
13. 方程组 的解为 .14. 今年五月某中学举行一次“新冠”防疫知识竞赛,该校九年级1班、2班各选派了6名学生参赛,为了全面了解、比较两个班级的参赛学生的实力,请你根据下表成绩对他们进行统计分析:1班
65
70
70
70
75
82
2班
55
70
70
75
80
82
请问 , (填“>”“=”或“<”)
15. 有一条抛物线,两位同学分别说了它的一个特点:甲:对称轴是直线x=4;乙:顶点到x轴的距离为2,请你写出一个符合条件的解析式: .16. 盒子里有甲、乙、丙三种粒子,若相同种类的两颗粒子发生碰撞,则变成一颗乙粒子;不同种类的两颗粒子发生碰撞,会变成第三种粒子,例如一颗甲粒子和一颗乙粒子发生碰撞则变成一颗丙粒子,现有甲粒子6颗,乙粒子4颗,丙粒子5颗,如果经过各种两两碰撞后,只剩下1颗粒子,给出下列结论:①最后一颗粒子可能是甲粒子;②最后一颗粒子一定不是乙粒子;③最后一颗粒子可能是丙粒子.其中正确结论的序号是: .三、解答题
-
17. 计算:18. 解不等式组: 并把解集表示在数轴上,19. 已知 ,求代数式 的值20. 下面是小明同学设计的“作一个角等于已知角的2倍”的尺规作图过程.

已知:∠AOB
求作:∠ADC , 使∠ADC=2∠AOB
作法:如图,
①在射线OB上任取一点C;
②作线段OC的垂直平分线,交OA于点D , 交OB于点E , 连接DC .
所以∠ADC即为所求的角
根据小明设计的尺规作图过程,
(1)、使用直尺和圆规,补全图形(保留作图痕迹)(2)、完成下面证明(说明:括号里填写作图依据)证明:∵DE是线段OC的垂直平分线,
∴OD= ▲ ( ▲ ).
∴∠AOB= ▲ ( ▲ ).
∵∠ADC=∠AOB+∠DCO ,
∴∠ADC=2∠AOB .
21. 已知关于x的一元二次方程 有两个不相等的实数根(1)、求a的取值范围;(2)、请你给出一个符合条件的a的值,并求出此时方程的解.22. 如图,矩形ABCD , 延长AD至点F , 使DF=AD , 连接AC , CF , 过点A作AE//CF交CD的延长线于点E , 连接EF . (1)、求证:四边形ACFE是菱形;(2)、连接BE交AD于点G当AB=2, 时,求BE的长.23. 为了解昌平区两校学生对垃圾分类知识的掌握情况,从甲、乙两所学校各随机抽取40名学生进行垃圾分类知识的测试,获得了他们的成绩(百分制)并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息
(1)、求证:四边形ACFE是菱形;(2)、连接BE交AD于点G当AB=2, 时,求BE的长.23. 为了解昌平区两校学生对垃圾分类知识的掌握情况,从甲、乙两所学校各随机抽取40名学生进行垃圾分类知识的测试,获得了他们的成绩(百分制)并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息a . 甲、乙两校40名学生成绩的频数分布统计表如下:
成绩x
学校
50≤x<60
60≤x<70
70≤x<80
80≤x<90
90≤x≤100
甲
4
15
9
10
2
乙
6
3
15
14
2
(说明:成绩80分及以上为优秀,70~79分为良好,60~69分为合格,60分以下为不合格)
b . 甲校成绩在70≤x<80这一组的是:70,70,71,72,73,74,76,77,79
c . 甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分
中位数
众数
甲
74.2
n
85
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)、写出表中n的值;(2)、估计乙校200名学生中,成绩优秀的学生人数是;(3)、假设甲校200名学生都参加此次测试,并决定年级排名在前100名的学生都可以被评为“垃圾分类知识标兵”荣誉称号,预估甲校学生至少要达到分可以获得此荣誉称号.24. 在平面直角坐标系xOy中,反比例函数 的图象与直线l:y=-x-2交于点A(a , -4),直线l与x轴交于点B .(1)、求a , k的值;(2)、在y轴上存在一点C , 使得 ,求点C的坐标.25. 如图,AB为⊙O直径,点C , D在⊙O上,且 ,过点C作CE//BD , 交AB延长线于点E . (1)、求证:CE为⊙O切线;(2)、过点C作CF⊥AE交BD于H点,∠E=30°,CH=6,求BE的长.26. 在平面直角坐标系xOy中,抛物线 与x轴的交点为点A(1,0)和点B .(1)、直接写出抛物线的对称轴和点B的坐标;(2)、分别过点P(t , 0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N , 记抛物线在M , N之间的部分为图象G(包括M , N两点),记图形G上任意一点的纵坐标的最大值是m , 最小值为n
(1)、求证:CE为⊙O切线;(2)、过点C作CF⊥AE交BD于H点,∠E=30°,CH=6,求BE的长.26. 在平面直角坐标系xOy中,抛物线 与x轴的交点为点A(1,0)和点B .(1)、直接写出抛物线的对称轴和点B的坐标;(2)、分别过点P(t , 0)和点Q(t+2,0)作x轴的垂线,交抛物线于点M和点N , 记抛物线在M , N之间的部分为图象G(包括M , N两点),记图形G上任意一点的纵坐标的最大值是m , 最小值为n①当a=2时,画出抛物线的图象,根据图象直接写出m-n的最小值;
②若存在实数t , 使得m-n=2,直接写出a的取值范围
27. 如图,在等腰直角△ABC中,AB=AC , ∠BAC=90°,点D是CA延长线上一点,点E是AB延长线上一点,且AD=BE , 过点A作DE的垂线交DE于点F , 交BC的延长线于点G (1)、依题意补全图形;(2)、当∠AED=α , 请你用含α的式子表示∠AGC;(3)、用等式表示线段CG与AD之间的数量关系,并写出证明思路28. 对于平面直角坐标系xOy中的图形M , N , 给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P , Q两点间的距离有最小值,那么称这个最小值为图形M , N间的“闭距离”,记作d(M , N),特殊地,当图形M与图形N有公共点时,规定d(M , N)=0
(1)、依题意补全图形;(2)、当∠AED=α , 请你用含α的式子表示∠AGC;(3)、用等式表示线段CG与AD之间的数量关系,并写出证明思路28. 对于平面直角坐标系xOy中的图形M , N , 给出如下定义:P为图形M上任意一点,Q为图形N上任意一点,如果P , Q两点间的距离有最小值,那么称这个最小值为图形M , N间的“闭距离”,记作d(M , N),特殊地,当图形M与图形N有公共点时,规定d(M , N)=0已知点 .
(1)、①求d(点O , 线段AB);②若d(线段CD , 直线AB)=1,直接写出m的值;
(2)、⊙O的半径为r , 若d(⊙O , 线段AB)≤1,直接写出r的取值范围;(3)、若直线 上存在点E , 使d(E , )=1,直接写出b的取值范围.