安徽省宣城市三校2021年中考数学3月模拟试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 下列运算错误的是( )A、 B、 C、 D、2. 不等式组 的解集在数轴上表示为( )A、
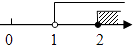 B、
B、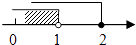 C、
C、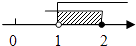 D、
D、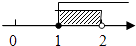 3. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、4. 用代数式表示“ 的2倍与 的平方的差”,正确的是( ).A、 B、 C、 D、5. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
3. 据统计,某城市去年接待旅游人数约为89000000人,89000000这个数据用科学记数法表示为( )A、 B、 C、 D、4. 用代数式表示“ 的2倍与 的平方的差”,正确的是( ).A、 B、 C、 D、5. 如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )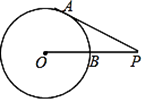 A、3 B、3 C、6 D、96. 某班班长统计去年1∼8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
A、3 B、3 C、6 D、96. 某班班长统计去年1∼8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )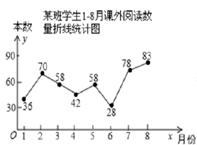 A、每月阅读数量的平均数是50 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月7. 如图,在 中, , ,DE垂直平分AB , 交BC于点E , ,则 ( )
A、每月阅读数量的平均数是50 B、众数是42 C、中位数是58 D、每月阅读数量超过40的有4个月7. 如图,在 中, , ,DE垂直平分AB , 交BC于点E , ,则 ( )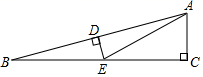 A、 B、 C、 D、8. 二次函数 的图象如图,给出下列四个结论:
A、 B、 C、 D、8. 二次函数 的图象如图,给出下列四个结论: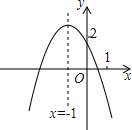
① ;② ;③方程 没有实数根;④ .
其中正确结论的个数是( )
A、4个 B、3个 C、2个 D、1个9. 已知a、b实数且满足(a2+b2)2﹣(a2+b2)﹣6=0,则a2+b2的值为( )A、3 B、﹣2 C、3或﹣2 D、﹣3或210. 如图,矩形ABCD中,AB=2AD=4cm , 动点P从点A出发,以1cm/s的速度沿线段AB向点B运动,动点Q同时从点A出发,以2cm/s的速度沿折线AD→DC→CB向点B运动,当一个点停止时另一个点也随之停止.设点P的运动时间是x(s)时,△APQ的面积是y(cm2),则能够反映y与x之间函数关系的图象大致是( )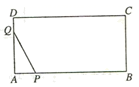 A、
A、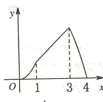 B、
B、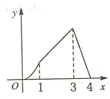 C、
C、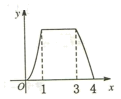 D、
D、
二、填空题
-
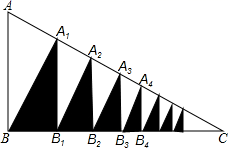
11. 已知 为实数,若 均为多项式 的因式,则 .12. 如图,在 中, , , ,过B作 ,过 作 ,得阴影 ;再过 作 ,过 作 ,得阴影 ;…如此下去.请猜测这样得到的所有阴影三角形的面积之和为 .
 13. 如图, 是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且 ,⊙O的半径为6,则点P到AC距离的最大值是 .
13. 如图, 是⊙O的内接三角形,且AB是⊙O的直径,点P为⊙O上的动点,且 ,⊙O的半径为6,则点P到AC距离的最大值是 . 14. 如图,图1是“杨辉三角”数阵;图2是(a+b)n的展开式(按b的升幂排列).若(1+x)45的展开式按x的升幂排列得:(1+x)45=a0+a1x+a2x2+…+a45x45 , 则a2= .
14. 如图,图1是“杨辉三角”数阵;图2是(a+b)n的展开式(按b的升幂排列).若(1+x)45的展开式按x的升幂排列得:(1+x)45=a0+a1x+a2x2+…+a45x45 , 则a2= .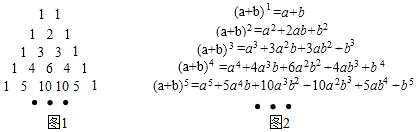
三、解答题
-
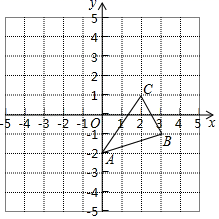
15. 计算:2cos45°+(﹣ )-1+(2020﹣ )0+|2﹣ |.16. 《九章算术》是中国传统数学重要的著作.《九章算术》中记载:“今有人共买鸡,人出八,盈三;人出七,不足四.问人数、鸡价各几何?”译文:“今天有几个人共同买鸡,每人出8钱,多余3钱,每人出7钱,还缺4钱.问人数和鸡的价钱各是多少?”请列方程组解决此问题.17. 在所给格点图中,画出△ABC作下列变换后的三角形,并写出所得到的三角形三个顶点的坐标.
⑴沿y轴正方向平移2个单位后得到△A1B1C1;
⑵关于y轴对称后得到△A2B2C2.
⑶以点B为位似中心,放大到2倍后得到△A3B3C3.
 18. 如图所示,小亮在大楼 的观光电梯中的 点测得大楼 楼底 点的俯角为60°,此时他距地面的高度 为21米,电梯再上升9米到达 点,此时测得大楼 楼顶 点的仰角为45°,求大楼 的高度.(结果保留根号)
18. 如图所示,小亮在大楼 的观光电梯中的 点测得大楼 楼底 点的俯角为60°,此时他距地面的高度 为21米,电梯再上升9米到达 点,此时测得大楼 楼顶 点的仰角为45°,求大楼 的高度.(结果保留根号)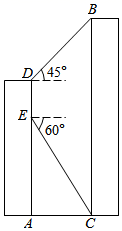 19. 在 中, , ,点C在直线m上, , ,其中点D、E分别在直线AC、m上,将 绕点B旋转 点D、E都不与点C重合 .
19. 在 中, , ,点C在直线m上, , ,其中点D、E分别在直线AC、m上,将 绕点B旋转 点D、E都不与点C重合 .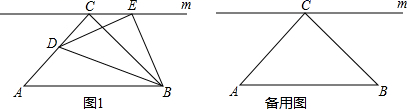 (1)、当点D在边AC上时 如图 ,设 , ,求y关于x的函数解析式,并写出定义域;(2)、当 为等腰三角形时,求CD的长.20. “时裳”服装店现有A、B、C三种品牌的衣服和D、E两种品牌的裤子,温馨家现要从服装店选购一种品牌的衣服和一种品牌的裤子.(1)、写出所有选购方案(利用树状图或列表方法表示)(2)、如果(1)中各种选购方案被选中的可能性相同,那么A品牌衣服被选中的概率是多少?21. 如图,以 的一边AB为直径作⊙O , ⊙O与BC边的交点D恰好为BC的中点,过点D作 .
(1)、当点D在边AC上时 如图 ,设 , ,求y关于x的函数解析式,并写出定义域;(2)、当 为等腰三角形时,求CD的长.20. “时裳”服装店现有A、B、C三种品牌的衣服和D、E两种品牌的裤子,温馨家现要从服装店选购一种品牌的衣服和一种品牌的裤子.(1)、写出所有选购方案(利用树状图或列表方法表示)(2)、如果(1)中各种选购方案被选中的可能性相同,那么A品牌衣服被选中的概率是多少?21. 如图,以 的一边AB为直径作⊙O , ⊙O与BC边的交点D恰好为BC的中点,过点D作 .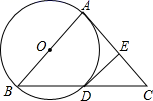 (1)、求证:DE为⊙O的切线;(2)、连接OC交DE于点F , 若 ,求 的值.22. 点E是矩形ABCD边AB延长线上的一动点,在矩形ABCD外作Rt△ECF,其中∠ECF=90°,过点F作FG⊥BC,交BC的延长线于点G,连接DF,交CG于点H.
(1)、求证:DE为⊙O的切线;(2)、连接OC交DE于点F , 若 ,求 的值.22. 点E是矩形ABCD边AB延长线上的一动点,在矩形ABCD外作Rt△ECF,其中∠ECF=90°,过点F作FG⊥BC,交BC的延长线于点G,连接DF,交CG于点H.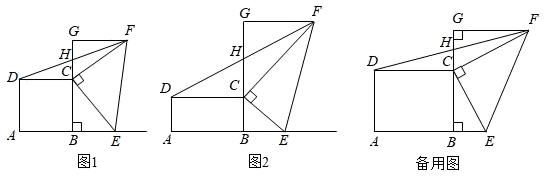 (1)、发现:如图1,若AB=AD,CE=CF,猜想线段DH与HF的数量关系是;(2)、探究:如图2,若AB=nAD,CF=nCE,则(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)、拓展:在(2)的基础上,若射线FC过AD的三等分点,AD=3,AB=4,则直接写出线段EF的长.23. 已知,抛物线 ,过 、 、 ,点 为顶点.
(1)、发现:如图1,若AB=AD,CE=CF,猜想线段DH与HF的数量关系是;(2)、探究:如图2,若AB=nAD,CF=nCE,则(1)中的猜想是否仍然成立?若成立,请给予证明;若不成立,请说明理由.(3)、拓展:在(2)的基础上,若射线FC过AD的三等分点,AD=3,AB=4,则直接写出线段EF的长.23. 已知,抛物线 ,过 、 、 ,点 为顶点. (1)、求抛物线的解析式及顶点 的坐标;(2)、在抛物线的对称轴上找一点 ,使 的值最小,并求出 的坐标;(3)、若直线 经过点 、 两点,且与 轴交于点 ,判断 的面积与 的面积是否相等?请说明理由.
(1)、求抛物线的解析式及顶点 的坐标;(2)、在抛物线的对称轴上找一点 ,使 的值最小,并求出 的坐标;(3)、若直线 经过点 、 两点,且与 轴交于点 ,判断 的面积与 的面积是否相等?请说明理由.