安徽省阜阳市太和县2021年中考数学一模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 下列各数中,最大的数是( )A、-π B、-3 C、0 D、12. 下列各式成立的是( )A、 B、 C、 D、3. 春节燃放爆竹是中华民族辞旧迎新的习俗,然而因春节期间全国各地雾霾天气频现,各地纷纷出台禁止燃放烟花爆竹的通知,如图所示的是一种爆竹的示意图,则爆竹的俯视图是( )
 A、
A、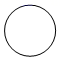 B、
B、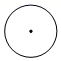 C、
C、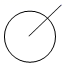 D、
D、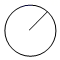 4. 关于 的不等式组 的整数解有( )A、6个 B、7个 C、8个 D、无数个5. 近日,安徽各县(市)相继发布2020年主要经济数据,县域经济总量(GDP)20强名单新鲜出炉.我县排名第9位,经济总量达到476亿元.数据476亿用科学记数法表示为( )A、 B、 C、 D、6. 一元二次方程 的解是( )A、 B、 , C、 , D、无实数解7. 如图,四边形 的对角线 , , , , 分别是 , , , 的中点,若在四边形 内任取一点,则这一点落在图中阴影部分的概率为( )
4. 关于 的不等式组 的整数解有( )A、6个 B、7个 C、8个 D、无数个5. 近日,安徽各县(市)相继发布2020年主要经济数据,县域经济总量(GDP)20强名单新鲜出炉.我县排名第9位,经济总量达到476亿元.数据476亿用科学记数法表示为( )A、 B、 C、 D、6. 一元二次方程 的解是( )A、 B、 , C、 , D、无实数解7. 如图,四边形 的对角线 , , , , 分别是 , , , 的中点,若在四边形 内任取一点,则这一点落在图中阴影部分的概率为( )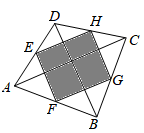 A、 B、 C、 D、8. 若反比例函数 的图象经过第二、第四象限,则关于 的一次函数 的图象可能是( )A、
A、 B、 C、 D、8. 若反比例函数 的图象经过第二、第四象限,则关于 的一次函数 的图象可能是( )A、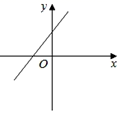 B、
B、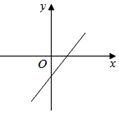 C、
C、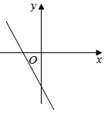 D、
D、 9. 如图, 的顶点在正方形网格的格点上,则 的值为( )
9. 如图, 的顶点在正方形网格的格点上,则 的值为( )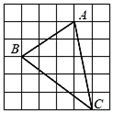 A、 B、 C、 D、10. 在 中, , 为 上一动点,若 , ,则 的最小值为( )
A、 B、 C、 D、10. 在 中, , 为 上一动点,若 , ,则 的最小值为( )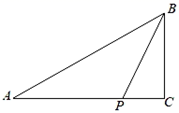 A、5 B、10 C、 D、
A、5 B、10 C、 D、二、填空题
-
11. 计算: .12. 因式分解: .13. 如图,平行四边形 的边 的中点 在 轴上,对角线 与 轴交于点 ,若反比例函数 ( )的图象恰好经过 的中点 ,且 的面积为6,则 的值为 .
 14. 如图1,E是等边 的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作等边 ,连接 已知 的面积(S)与BE的长(x)之间的函数关系如图2所示( 为抛物线的顶点).
14. 如图1,E是等边 的边BC上一点(不与点B , C重合),连接AE , 以AE为边向右作等边 ,连接 已知 的面积(S)与BE的长(x)之间的函数关系如图2所示( 为抛物线的顶点). (1)、当 的面积最大时, 的大小为 .(2)、等边 的边长为 .
(1)、当 的面积最大时, 的大小为 .(2)、等边 的边长为 .三、解答题
-
15. 解分式方程: = .16. 如图,在平面直角坐标系内, 的三个顶点坐标分别为 , , .
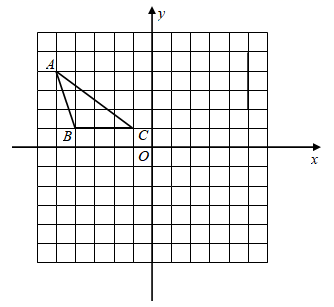
⑴作出 关于 轴对称的 .
⑵作出 绕点 按顺时针方向旋转90°得到的 .
17. 《孙子算经》是中国古代的数学著作,成书大约一千五百年前.卷中举例说明筹算分数算法和筹算开平方法,其中“物不知数”的问题.在西方的数学史里被称为“中国的剩余定理”.《孙子算经》中有一道题:“今有木,不知长短,引绳度之,余绳四尺五,屈绳量之,不足一尺,问木长几何?”大致意思是“用一根绳子去量一根木条,绳子剩余4.5尺,将绳子对折再量木条,木条剩余1尺,向木条长多少尺?”18. 为建设新农村,全面实现“村村亮”,某市在其辖区内的每个村庄都安装了如图1所示的太阳能路灯,图2是该路灯的平面示意图, 为立柱的一部分,灯臂 ,支架 与立柱 分别交于A , B两点,灯臂 与支架 交于点C . 已知 , ,求点C到地面的距离.(结果精确到 .参考数据: , , )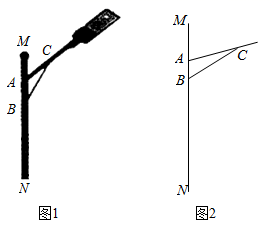 19. 观察以下等式:
19. 观察以下等式:第一个等式:
第二个等式:
第三个等式:
…
按照上述规律,解决下列问题:
(1)、写出第四个等式 .(2)、写出你猜想的第 个等式: ▲ (用含 的等式表示),并证明.20. 如图,以 为底的等腰 的三个顶点都在 上,过点 A作 交 的反向延长线于点D . (1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.21. 随着手机APP技术的迅猛发展,春节期间人们的娱乐方式比以往有很多改变.某校数学兴趣小组为了解某社区居民对各类APP的使用情况,针对给出的四类APP( 看电影或电视、 刷抖音、 聊天、 其他)对社区内部分居民进行了抽样调查(每人必选且只能选择其中一项).根据调查结果绘制了如图所示的不完整的统计图,请你根据图中信息解答下列问题:
(1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.21. 随着手机APP技术的迅猛发展,春节期间人们的娱乐方式比以往有很多改变.某校数学兴趣小组为了解某社区居民对各类APP的使用情况,针对给出的四类APP( 看电影或电视、 刷抖音、 聊天、 其他)对社区内部分居民进行了抽样调查(每人必选且只能选择其中一项).根据调查结果绘制了如图所示的不完整的统计图,请你根据图中信息解答下列问题: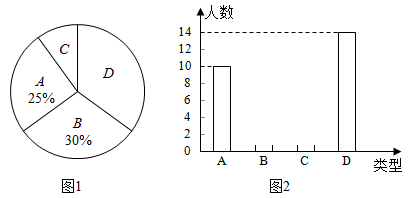 (1)、参与抽样调查的总人数是 .(2)、补全条形统计图.(3)、若小明和小红两人在四类APP中随机选择一类进行使用,则小明和小红恰好选择同一类APP的概率为多少?22. 如图,抛物线 : 交 轴正半轴于点 ,将抛物线 先向右平移3个单位,再向上平移3个单位得到抛物线 , 与 交于点 ,直线 交 于点 .
(1)、参与抽样调查的总人数是 .(2)、补全条形统计图.(3)、若小明和小红两人在四类APP中随机选择一类进行使用,则小明和小红恰好选择同一类APP的概率为多少?22. 如图,抛物线 : 交 轴正半轴于点 ,将抛物线 先向右平移3个单位,再向上平移3个单位得到抛物线 , 与 交于点 ,直线 交 于点 .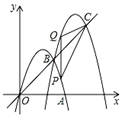 (1)、①抛物线 的解析式为 ▲ ;
(1)、①抛物线 的解析式为 ▲ ;②求点 , 的坐标.
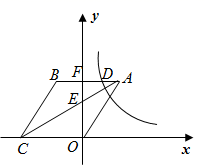
(2)、 是抛物线 间的点,作 轴交抛物线 于点 ,连接 , .设点 的横坐标为 ,当 为何值时,使 的面积最大?并求出最大值.23. 如图1,在正方形 中, 为对角线 的中点, 为边 上一动点,连接 交 于点 ,过点 作 垂足为 ,连接 ,过点 作 交 于点 .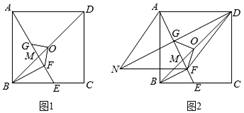 (1)、若 为 的中点,求 的值.(2)、证明: .(3)、如图2,连接 并延长至 ,使 ,连接 , , ,若四边形 是菱形, ,求 的长.
(1)、若 为 的中点,求 的值.(2)、证明: .(3)、如图2,连接 并延长至 ,使 ,连接 , , ,若四边形 是菱形, ,求 的长.