安徽省阜阳市阜南县2021年中考数学模拟试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、单选题
-
1. 在 ,1, , 四个数中,最小的数是( )A、0 B、1 C、 D、-12. 下列计算中,正确的是( )A、 B、 C、 D、3. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每300万年误差1秒.数300万用科学记数法表示为( )A、 B、 C、 D、30×1054. 如图所示的几何体的从上面看到的形状图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )
5. 如图,在 中, , , , ,连接BC,CD,则 的度数是( )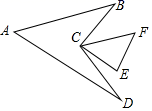 A、45° B、50° C、55° D、80°6. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变7. 若关于x的一元二次方程x2+(m+2)x=0有两个相等的实数根,则实数m的值为( )A、2 B、﹣2 C、﹣2或2 D、﹣1或38. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、9. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、1510. 如图所示,正方形 的边长为 ,点 分别为边 的中点,动点 从点 向点 运动, 到点 时停止运动;同时,动点 从点 出发,沿 运动,已知点 的运动速度相同,设点 的运动路程为 的面积为 ,则能大致表示 与 的函数关系的图象是( )
A、45° B、50° C、55° D、80°6. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分,方差s2=41.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变7. 若关于x的一元二次方程x2+(m+2)x=0有两个相等的实数根,则实数m的值为( )A、2 B、﹣2 C、﹣2或2 D、﹣1或38. 当 时,二次函数 的图象与x轴所截得的线段长度之和为( )A、 B、 C、 D、9. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、1510. 如图所示,正方形 的边长为 ,点 分别为边 的中点,动点 从点 向点 运动, 到点 时停止运动;同时,动点 从点 出发,沿 运动,已知点 的运动速度相同,设点 的运动路程为 的面积为 ,则能大致表示 与 的函数关系的图象是( )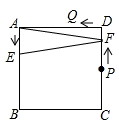 A、
A、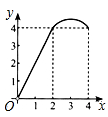 B、
B、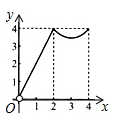 C、
C、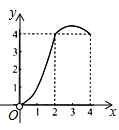 D、
D、
二、填空题
-
11. 分解因式: .12. 如图,圆锥的底面半径OB为5cm,它的侧面展开图扇形的半径AB为15cm,则这个扇形的圆心角的度数为 .
 13. 如图,平行于y轴的直尺(部分)与反比例函数 的图象交于A,C两点,与x轴交于B,D两点,连结 ,点A,B对应直尺上的刻度分别为5,2,直尺的宽度 , ,则点C的坐标是.
13. 如图,平行于y轴的直尺(部分)与反比例函数 的图象交于A,C两点,与x轴交于B,D两点,连结 ,点A,B对应直尺上的刻度分别为5,2,直尺的宽度 , ,则点C的坐标是. 14. 如图,已知 中, ,点M、N分别在线段 、 上,将 沿直线 折叠,使点A的对应点D恰好落在线段 上.
14. 如图,已知 中, ,点M、N分别在线段 、 上,将 沿直线 折叠,使点A的对应点D恰好落在线段 上. (1)、当四边形 为平行四边形时,则平行四边形 必为;(2)、当 为直角三角形时,则折痕 的长为 .
(1)、当四边形 为平行四边形时,则平行四边形 必为;(2)、当 为直角三角形时,则折痕 的长为 .三、解答题
-
15. 化简并求值: ,其中 .16. 清朝数学家梅文鼎的《方程论》中有这样一题:山田三亩,场地六亩,共折实田四亩七分;又山田五亩,场地三亩,共折实田五亩五分,问每亩山田折实田多少,每亩场地折实田多少?
译文为:若有山田3亩,场地6亩,其产粮相当于实田4.7亩;若有山田5亩,场地3亩,其产粮相当于实田5.5亩,问每亩山田和每亩场地产粮各相当于实田多少亩?
17. 如图, 三个顶点的坐标分别为 . (1)、请画出 关于x轴对称的 ;(2)、请画出 绕点B逆时针旋转 后的 ;(3)、用无刻度尺作图,求作线段 的中点P .18. 观察以下等式:
(1)、请画出 关于x轴对称的 ;(2)、请画出 绕点B逆时针旋转 后的 ;(3)、用无刻度尺作图,求作线段 的中点P .18. 观察以下等式:第1个等式: =1,
第2个等式: ,
第3个等式: ,
第4个等式: ,
第5个等式: ,
……
按照以上规律,解决下列问题:
(1)、写出第6个等式: .(2)、写出你猜想的第n个等式: ▲ (用含n的式子表示),并证明其正确性.19. 某兴趣小组为了测量大楼 的高度,先沿着斜坡 走了 米到达坡顶点 处,然后在点 处测得大楼顶点 的仰角为 ,已知斜坡 的坡度为 ,点 到大楼的距离 为 米,求大楼的高度 .(参考数据: , , )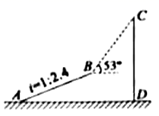 20. 如图,以 为底的等腰 的三个顶点都在 上,过点 A作 交 的反向延长线于点D .
20. 如图,以 为底的等腰 的三个顶点都在 上,过点 A作 交 的反向延长线于点D . (1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.21. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:
(1)、求证: 是 的切线;(2)、若四边形 是平行四边形,且 ,求 的半径.21. 根据公安部交管局下发的通知,自2020年6月1日起,将在全国开展“一带一盔”安全守护行动,其中就要求骑行摩托车、电动车需要佩戴头盔.某日我市交警部门在某个十字路口共拦截了50名不带头盔的骑行者,根据年龄段和性别得到如下表的统计信息,根据表中信息回答下列问题:年龄 (岁)
人数
男性占比
4
50%
60%
25
60%
8
75%
3
100%
(1)、统计表中 的值为;(2)、若要按照表格中各年龄段的人数来绘制扇形统计图,则年龄在“ ”部分所对应扇形的圆心角的度数为;(3)、在这50人中女性有人;(4)、若从年龄在“ ”的4人中随机抽取2人参加交通安全知识学习,请用列表或画树状图的方法,求恰好抽到2名男性的概率.


