广东省深圳市福田区2021年中考数学三模试卷
试卷更新日期:2021-06-11 类型:中考模拟
一、选择题:(每小题3分,共计30分)
-
1. 的倒数是( )A、-2 B、2 C、 D、2. 下列图形中,是中心对称图形的是( )A、
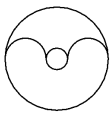 B、
B、 C、
C、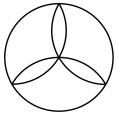 D、
D、 3. 如图,某几何体由6个大小相同的小立方体搭成,则它的左视图是( )
3. 如图,某几何体由6个大小相同的小立方体搭成,则它的左视图是( ) A、
A、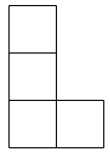 B、
B、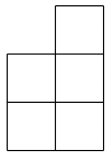 C、
C、 D、
D、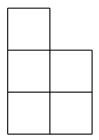 4. 下列计算正确的是( )A、 B、 C、 D、5. 不等式组 的解集是( )A、x≤2 B、x>-1 C、x<-1 D、-1<x≤26. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,刚好两车空出来;每车坐2人,多出9人无车坐.求人数和车数各多少?根据题意,设车有x辆,则可列出方程()A、3x-2=2x+9 B、3(x-2)=2x+9 C、 D、3(x-2)=2(x+9)7. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=39.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩与该班39人的测试成绩相比,下列说法正确的是( )A、平均分不变,方差变小 B、平均分不变,方差变大 C、平均分和方差都不变 D、平均分和方差都改变8. 如图,在Rt△ABC中,∠B=90°,AC=5,AB=3,点E是边CB上一动点,过点E作EF∥CA交AB于点F,D为线段EF的中点,按下列步骤作图:①以C为圆心,适当长为半径画弧交CB,CA于点M,点N;②分别以M,N为圆心,适当长为半径画弧,两弧的交点为G;③作射线CG.若射线CG经过点D,则CE的长度为( )
4. 下列计算正确的是( )A、 B、 C、 D、5. 不等式组 的解集是( )A、x≤2 B、x>-1 C、x<-1 D、-1<x≤26. 我国古代数学著作《孙子算经》中有“多人共车”问题:今有三人共车,二车空;二人共车,九人步.问人与车各几何?其大意是:每车坐3人,刚好两车空出来;每车坐2人,多出9人无车坐.求人数和车数各多少?根据题意,设车有x辆,则可列出方程()A、3x-2=2x+9 B、3(x-2)=2x+9 C、 D、3(x-2)=2(x+9)7. 某班有40人,一次体能测试后,老师对测试成绩进行了统计.由于小亮没有参加本次集体测试,因此计算其他39人的平均分为90分,方差s2=39.后来小亮进行了补测,成绩为90分,关于该班40人的测试成绩与该班39人的测试成绩相比,下列说法正确的是( )A、平均分不变,方差变小 B、平均分不变,方差变大 C、平均分和方差都不变 D、平均分和方差都改变8. 如图,在Rt△ABC中,∠B=90°,AC=5,AB=3,点E是边CB上一动点,过点E作EF∥CA交AB于点F,D为线段EF的中点,按下列步骤作图:①以C为圆心,适当长为半径画弧交CB,CA于点M,点N;②分别以M,N为圆心,适当长为半径画弧,两弧的交点为G;③作射线CG.若射线CG经过点D,则CE的长度为( )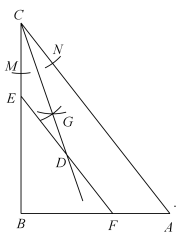 A、 B、 C、 D、9. 如图,抛物线 的顶点坐标为(1,n).下列结论:① ;② ;③关于x的一元二次方程 有两个不相等实数根;④抛物线上有两点 和 若 且 ,则 ,其中正确的结论共有( )
A、 B、 C、 D、9. 如图,抛物线 的顶点坐标为(1,n).下列结论:① ;② ;③关于x的一元二次方程 有两个不相等实数根;④抛物线上有两点 和 若 且 ,则 ,其中正确的结论共有( )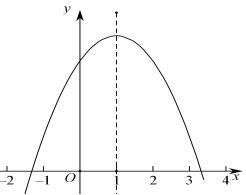 A、1个 B、2个 C、3个 D、4个10. 如图,在反比例函数 的图象上有动点A,连接OA, 的图象经过OA的中点B,过点B作BC∥x轴交函数 的图象于点C,过点C作CE∥y轴交函数 的图象于点D,交x轴点E,连接AC,OC,BD,OC与BD交于点F.下列结论:①k=1;② ;③ ,④若BD=AO,则∠AOC=2∠COE.其中正确的是( )
A、1个 B、2个 C、3个 D、4个10. 如图,在反比例函数 的图象上有动点A,连接OA, 的图象经过OA的中点B,过点B作BC∥x轴交函数 的图象于点C,过点C作CE∥y轴交函数 的图象于点D,交x轴点E,连接AC,OC,BD,OC与BD交于点F.下列结论:①k=1;② ;③ ,④若BD=AO,则∠AOC=2∠COE.其中正确的是( )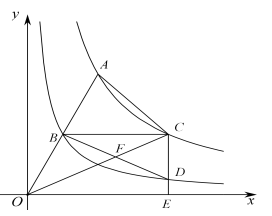 A、①③④ B、②③④ C、①②④ D、①②③④
A、①③④ B、②③④ C、①②④ D、①②③④二、填空题:(每小题3分,共计15分)
-
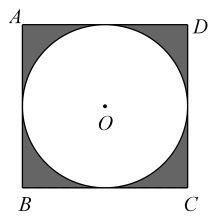
11. 因式分解: .12. 如图,⊙O与正方形ABCD各边相切,若随机向正方形内投一粒米(将米粒看成一个点),则米粒落在阴影部分的概率是 .
 13. 如图,AB是一座办公大楼,一架无人机从C处测得楼顶部B的仰角为60°,测得楼底部A的俯角为37°,测得与大楼的水平距离为40米,则该办公大楼的高度是米.(结果保留整数,参考数据: ≈1.73,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)
13. 如图,AB是一座办公大楼,一架无人机从C处测得楼顶部B的仰角为60°,测得楼底部A的俯角为37°,测得与大楼的水平距离为40米,则该办公大楼的高度是米.(结果保留整数,参考数据: ≈1.73,sin37°≈0.6,cos37°≈0.8,tan37°≈0.75)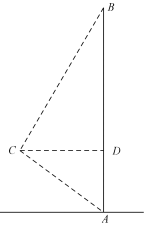 14. 定义:如图1,已知锐角∠AOB内有定点P,过点P任意作一条直线MN,分别交射线OA,OB于点M,N.若P是线段MN的中点时,则称直线MN是∠AOB的中点直线.如图2,射线OQ的表达式为y=2x(x>0),射线OQ与x轴正半轴的夹角为∠α,P(3,1),若MN为∠α的中点直线,则直线MN的表达式为 .
14. 定义:如图1,已知锐角∠AOB内有定点P,过点P任意作一条直线MN,分别交射线OA,OB于点M,N.若P是线段MN的中点时,则称直线MN是∠AOB的中点直线.如图2,射线OQ的表达式为y=2x(x>0),射线OQ与x轴正半轴的夹角为∠α,P(3,1),若MN为∠α的中点直线,则直线MN的表达式为 .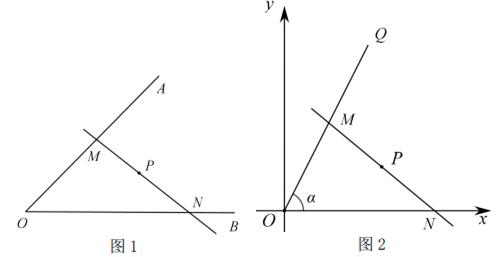 15. 如图,矩形纸片ABCD,AD=2AB=4,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为 .
15. 如图,矩形纸片ABCD,AD=2AB=4,点F在线段AD上,将△ABF沿BF向下翻折,点A的对应点E落在线段BC上,点M,N分别是线段AD与线段BC上的点,将四边形CDMN沿MN向上翻折,点C恰好落在线段BF的中点C'处,则线段MN的长为 .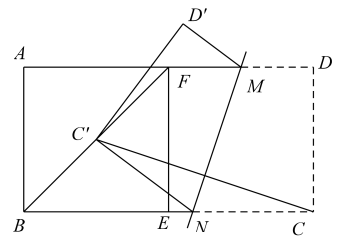
三、解答题:(本题共7小题,其中第16题5分,第17题6分,第18题8分,第19题8分,第20题8分,第21题10分,第22题10分,共55分)
-
16. 计算:17. 先化简: 再在-2,0,1,2四个数中选一个合适的数作为x的取值代入求值.18. 某学校开展了防疫知识的宣传教育活动.为了解这次活动的效果,学校从全校1500名学生中随机抽取部分学生进行知识测试(测试满分100分,得分x均为不小于60的整数),并将测试成绩分为四个等级:基本合格(60≤x<70),合格(70≤x<80),良好(80≤x<90),优秀(90≤x≤100),制作了如下统计图(部分信息未给出).
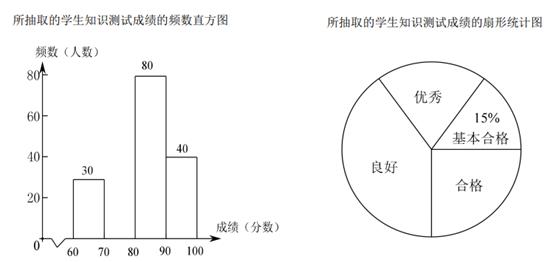
由图中给出的信息解答下列问题:
(1)、抽取学生的总人数为人;(2)、补全频数直方图;(3)、扇形统计图中“良好”所对应的扇形圆心角的度数是°;(4)、这次测试成绩的中位数会落在等级;(5)、如果全校学生都参加测试,请你根据抽样测试的结果,估计该校获得优秀的学生有多少人?19. 如图,⊙O的内接四边形ABED中,∠BAD=90°,AB=AE,AD,BE的延长线相交于点C,DF是⊙O的切线.
 (1)、求证:FD=FC;(2)、若EF=3,DE=4,求AB的长.20. 某市计划对道路进行维护.已知甲工程队每天维护道路的长度比乙工程队每天维护道路的长度多50%,甲工程队单独维护30千米道路的时间比乙工程队单独维护24千米道路的时间少用1天.(1)、求甲、乙两工程队每天维护道路的长度是多少千米?(2)、若某市计划对200千米的道路进行维护,每天需付给甲工程队的费用为25万元,每天需付给乙工程队的费用为15万元,考虑到要不超过26天完成整个工程,因工程的需要,两队均需参与,该市安排乙工程队先单独完成一部分,剩下的部分两个工程队再合作完成.问乙工程队先单独做多少天,该市需付的整个工程费用最低?整个工程费用最低是多少万元?21. 如图
(1)、求证:FD=FC;(2)、若EF=3,DE=4,求AB的长.20. 某市计划对道路进行维护.已知甲工程队每天维护道路的长度比乙工程队每天维护道路的长度多50%,甲工程队单独维护30千米道路的时间比乙工程队单独维护24千米道路的时间少用1天.(1)、求甲、乙两工程队每天维护道路的长度是多少千米?(2)、若某市计划对200千米的道路进行维护,每天需付给甲工程队的费用为25万元,每天需付给乙工程队的费用为15万元,考虑到要不超过26天完成整个工程,因工程的需要,两队均需参与,该市安排乙工程队先单独完成一部分,剩下的部分两个工程队再合作完成.问乙工程队先单独做多少天,该市需付的整个工程费用最低?整个工程费用最低是多少万元?21. 如图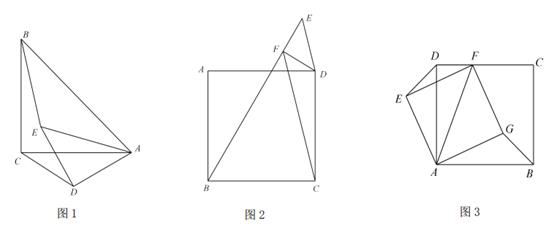 (1)、问题背景:如图1,∠ACB=∠ADE=90°,AC=BC,AD=DE.求证:△ABE∽△ACD;(2)、尝试应用:如图2,E为正方形ABCD外一点,∠BED=45°,过点D作DF⊥BE,垂足为F,连接CF.求 的值;(3)、拓展创新:如图3,四边形ABCD是正方形,点F是线段CD上一点,以AF为对角线作正方形AEFG,连接DE,BG.当DF=1, 时,则BG的长为 .22. 如图
(1)、问题背景:如图1,∠ACB=∠ADE=90°,AC=BC,AD=DE.求证:△ABE∽△ACD;(2)、尝试应用:如图2,E为正方形ABCD外一点,∠BED=45°,过点D作DF⊥BE,垂足为F,连接CF.求 的值;(3)、拓展创新:如图3,四边形ABCD是正方形,点F是线段CD上一点,以AF为对角线作正方形AEFG,连接DE,BG.当DF=1, 时,则BG的长为 .22. 如图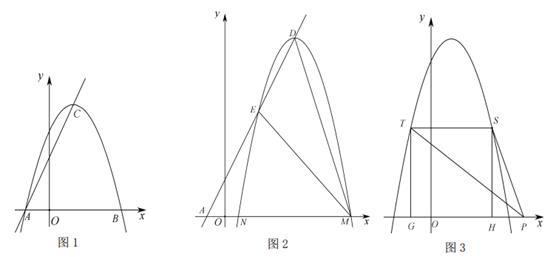
如图1,抛物线C1: 与x轴交于A(-1,0),B(3,0)两点,且顶点为C,直线y=kx+2经过A,C两点.
(1)、求直线AC的表达式与抛物线C1的表达式;(2)、如图2,将抛物线C1沿射线AC方向平移一定距离后,得到抛物线为C2 , 其顶点为D,抛物线C2与直线y=kx+2的另一交点为E,与x轴交于M,N两点(M点在N点右边),若 ,求点D的坐标;(3)、如图3,若抛物线C1向上平移4个单位得到抛物线C3 , 正方形GHST的顶点G,H在x轴上,顶点S,T在x轴上方的抛物线C3上,P(m,0)是射线GH上一动点,则正方形GHST的边长为 , 当m=时, 有最小值 .