广西北部湾经济区2021年中考数学七模试卷
试卷更新日期:2021-06-10 类型:中考模拟
一、选择题(共12小题,每小题3分,共36分。在每小题给出的四个选项中只有一项是符合要求的,用2B铅笔把答题卡.上对应题目的答案标号涂黑。)
-
1. 计算(-2a2)3的结果是( )A、-6a6 B、6a6 C、8a6 D、-8a62. 下列城市地铁的标志图案中,既是中心对称又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )A、x2·x3=x6 B、3x2+x2=4x4 C、(-x2)3=-x6 D、x6÷x2=x34. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
3. 下列运算正确的是( )A、x2·x3=x6 B、3x2+x2=4x4 C、(-x2)3=-x6 D、x6÷x2=x34. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、 C、
C、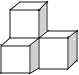 D、
D、 5. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E。若∠E=35°,则∠EAC的度数是( )
5. 如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E。若∠E=35°,则∠EAC的度数是( ) A、40° B、65° C、70° D、75°6. 不等式组 的解集为( )A、x<-3 B、x≤2 C、-3<x≤2 D、无解7. 若点A(x1 , -2),B(x2 , 3),C(x3 , 4)在反比例函数y= 的图象上,则x1 , x2 , x3的大小关系是( )A、x1<x2<x3 B、x1<x3<x2 C、x2<x1<x3 D、x3<x2<x18. 如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( )
A、40° B、65° C、70° D、75°6. 不等式组 的解集为( )A、x<-3 B、x≤2 C、-3<x≤2 D、无解7. 若点A(x1 , -2),B(x2 , 3),C(x3 , 4)在反比例函数y= 的图象上,则x1 , x2 , x3的大小关系是( )A、x1<x2<x3 B、x1<x3<x2 C、x2<x1<x3 D、x3<x2<x18. 如图,点A、B、C、D都在边长为1的网格格点上,以A为圆心,AE为半径画弧,弧EF经过格点D,则扇形AEF的面积是( ) A、 B、 C、π D、9. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为 ,由此可知小宇此次实心球训练的成绩为( )
A、 B、 C、π D、9. 在中考体育训练期间,小宇对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系式为 ,由此可知小宇此次实心球训练的成绩为( ) A、 米 B、8米 C、10米 D、2米10. 小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )A、 B、 C、 D、11. 我国古代数学家赵爽的弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么cosθ的值为( )
A、 米 B、8米 C、10米 D、2米10. 小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )A、 B、 C、 D、11. 我国古代数学家赵爽的弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如图,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较大的锐角为θ,那么cosθ的值为( ) A、 B、 C、 D、12. 如图,半径为A的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F,当点E从点B出发逆时针运动到点C时,点F经过的路径长是( )
A、 B、 C、 D、12. 如图,半径为A的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F,当点E从点B出发逆时针运动到点C时,点F经过的路径长是( ) A、 B、 C、 D、2 π
A、 B、 C、 D、2 π二、填空题(本小题共6小题,每小题3分,共18分)
-
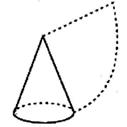
13. 因式分解:m3-6m2+9m=14. “北斗三号”最后一颗全球组网卫星的授时精度小于0.00000002秒,则0.00000002用科学记数法表示为15. 样本数据1,5,n,6,8的众数是1,则这组数的中位数是16. 小华为参加毕业晚会演出,准备制一项圆锥形彩色纸帽,如图所示,如果纸帽的底面半径为8cm,母线长为25cm,那么制作这顶纸帽至少需要彩色纸板的面积为 cm2。(结果保留π)
 17. 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 照此规律作下去,则点B2020的纵坐标为
17. 如图,在平面直角坐标系中有一边长为1的正方形OABC,边OA、OC分别在x轴、y轴上,如果以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 照此规律作下去,则点B2020的纵坐标为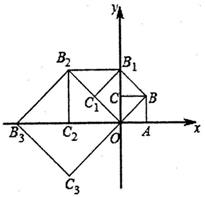 18. 如图,△CAB与△CDE均是等腰直角三角形,并且∠ACB=∠DCE=90°。连接BE,AD的延长线与BC、BE的交点分别是点G与点F,且AF⊥BE,将△CDE绕点C旋转直至CD∥BE时,若DA=4.5,DG=2,则BF的值是
18. 如图,△CAB与△CDE均是等腰直角三角形,并且∠ACB=∠DCE=90°。连接BE,AD的延长线与BC、BE的交点分别是点G与点F,且AF⊥BE,将△CDE绕点C旋转直至CD∥BE时,若DA=4.5,DG=2,则BF的值是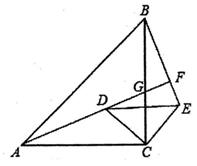
三、解答题(本大题共8小题,共66分。解答应写出文字说明或验算步骤)
-
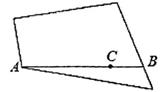
19. 计算:4×(- )2-23÷(-8)20. 解方程:x2-4x+2=021. 小明在书店-本书上看到下面材料:木工师傅有一块如图所示的四边形木板,他在木板上画出一条裁割线AB,现根据木板的情况,要过AB上的一点C,作出AB的垂线,用锯子进行裁割,然而手头没有直角尺,请你利用尺规作图帮助木工师傅在木板上过点C作AB的垂线(在木板上保留作图痕迹,不写作法)
 22. 某校对九年级400名学生进行了一次体育测试,并随机抽取甲、乙两个班各50名学生的测试成绩(成绩均为整数,满分50分)进行整理、描述和分析。
22. 某校对九年级400名学生进行了一次体育测试,并随机抽取甲、乙两个班各50名学生的测试成绩(成绩均为整数,满分50分)进行整理、描述和分析。下面给出了部分信息。(用x表示成绩,数据分成5组:A:30≤x<34,B:34≤x<38,C:38≤x<42,D:42≤x<46,E:46≤x≤50)
乙班成绩在D组的具体分数是:
42 42 42 42 42 42 42 42 42 42 43 44 45 45
甲,乙两班成绩统计表:
班级
甲班
乙班
平均分
44.1
44.1
中位数
44.5
n
众数
m
42
方差
7.7
17.4

根据以上信息,回答下列问题:
(1)、直接写出m、n的值;(2)、小明这次测试成绩是43分,在班上排名属中游略偏上,小明是甲、乙哪个班级学生?说明理由;(3)、假设该校九年级学生都参加此次测试,成绩达到45分及45分以上为优秀,估计该校本次测试成绩优秀的学生人数。23. 有一种落地晾衣架如图1所示,其原理是通过改变两根支撑杆夹角a的度数来调整晾杆的高度,图2是晾衣架的侧面的平面示意图,AB和CD分别是两根长度不等的支撑杆,夹角∠BOD=a,AO=70cm,BO=DO=80cm,CO=40cm。 (1)、若a=56°,求点A离地面的高度AE;
(1)、若a=56°,求点A离地面的高度AE;(参考值:sin62°=cos28°≈0.88,sin28°=cos62°≈0.47,tan62°≈1.88,tan28°≈0.53)
(2)、调节a的大小,使A离地面高度AE=125cm时,求此时C点离地面的高度CF。24. 某公司生产A型活动板房成本是每个425元。图①表示A型活动板房的一面墙,它由长方形和抛物线构成,长方形的长AD=4m,宽AB=3m,抛物线的最高点E到BC的距离为4m。 (1)、按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k+0)表示,求该抛物线的函数表达式;(2)、现将A型活动板房改造为B型活动板房。如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2。已知GM= 2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A
(1)、按如图①所示的直角坐标系,抛物线可以用y=kx2+m(k+0)表示,求该抛物线的函数表达式;(2)、现将A型活动板房改造为B型活动板房。如图②,在抛物线与AD之间的区域内加装一扇长方形窗户FGMN,点G,M在AD上,点N,F在抛物线上,窗户的成本为50元/m2。已知GM= 2m,求每个B型活动板房的成本是多少?(每个B型活动板房的成本=每个A型活动板房的成本+扇窗户FGMN的成本)
(3)、根据市场调查,以单价650元销售(2)中的B型活动板房,每月能售出100个,而单价每降低10元,每月能多售出20个。公司每月最多能生产160个B型活动板房。不考虑其他因素,公司将销售单价n(元)定为多少时,每月销售B型活动板房所获利润w(元)最大?最大利润是多少?25. 问题情境: (1)、如图1,已知正方形ABCD,点E在CD的延长线上,以CE为边构造正方形CEFG,连接BE和DG,则BE和DG的关系为。(2)、继续探究:如图2,若正方形ABCD的边长为3,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE。
(1)、如图1,已知正方形ABCD,点E在CD的延长线上,以CE为边构造正方形CEFG,连接BE和DG,则BE和DG的关系为。(2)、继续探究:如图2,若正方形ABCD的边长为3,点E是AD边上的一个动点,以CE为边在CE的右侧作正方形CEFG,连接DG、BE。①求证:DG⊥BE。
②连接BG,若AE=1,求BG长。
26. 如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0)、点C(8,0)两点,与y轴交于点A。 (1)、求二次函数的表达式;(2)、连接AC、AB,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)、连接OM,在(2)的结论下,线段AC上有一动点P,连接PM,求PM+ PC的值最小时,点P的坐标。
(1)、求二次函数的表达式;(2)、连接AC、AB,若点N在线段BC上运动(不与点B、C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;(3)、连接OM,在(2)的结论下,线段AC上有一动点P,连接PM,求PM+ PC的值最小时,点P的坐标。