广西贵港市覃塘区2021年中考数学三模试卷

试卷更新日期：2021-06-10 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12小题，每小题3分，共36分）每小题都给出标号为A、B、C、D的四个选项，其中只有一个是正确的.请考生用 2B铅笔在答题卡上将选定的答案标号涂黑.

1. 计算-2²的结果为

A、-2 B、-4 C、2 D、4

查看试题解析
2. 如图是由大小相同的小正方体搭成的几何体从上向下看得到的平面图形，小正方形中的数字表示该位置上小正方体的个数，则从左向右看得到的平面图形是

A、 B、 C、 D、

查看试题解析
3. 小王参加某企业招聘测试，他的笔试、面试、技能操作的成绩分别为 85分、80 分、90分，若依次按照 2∶ 3∶ 5 的比例确定总成绩，则小王的总成绩为（）

A、255分 B、84分 C、84.5 分 D、86 分

查看试题解析
4. 若分式 $\frac{x^{2} - 1}{x^{2} - 2 x + 1}$ 的值为0，则x 的值为

A、±1 B、-1 C、1 D、±2

查看试题解析
5. 下列计算正确的是

A、2x² $•$ 3x³=6x⁶ B、（y-2）²=y²-4 C、2y³-6y^²=-4y D、（-y²）³=-y⁶

查看试题解析
6. 若点 A（x-2，3）与点B（x+4，y-5）关于原点对称，则

A、x=-1，y=2 B、x=-1，y=8 C、x=-1，y=-2 D、x=1，y=8

查看试题解析
7. 若一元二次方程x²-3x=4的两个实数根分别为x₁和x₂ ，则x₁x₂的值为

A、-3 B、3 C、-4 D、4

查看试题解析
8. 下列四个命题中，正确命题的个数是
①若ac>bc，则a>b;②一组对角相等一组对边平行的四边形是平行四边形;③平分弦的直径垂直于弦;④反比例函数y= $\frac{k}{x}$ ，当k<0 时，y 随x的增大而增大.

A、4 B、3 C、2 D、1

查看试题解析
9. 如图，点A，B，C在⊙O上，CD⊥OA，CE⊥OB，垂足分别为D，E，若∠DCE=40°则∠ACB的度数为

A、140° B、110° C、80° D、70°

查看试题解析
10. 如图，点 A在函数y= $\frac{k}{x}$ （x>0）的图象上，AB⊥x轴于点 B，过线段AO 的三等分点M，N分别作x轴的平行线交AB于点P，Q.若S_{四边形MNQP}= 3，则k的值为

A、9 B、12 C、15 D、18

查看试题解析
11. 如图，线段 OA绕点O旋转，线段 OB的位置保持不变，在AB的上方作等边△PAB，若 OA=1，OB=3，则在线段 OA旋转过程中，线段 OP的最大值是

A、 $\sqrt{10}$ B、4 C、2 $\sqrt{5}$ D、5

查看试题解析
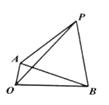12. 如图，在正方形ABCD中，动点E在BC边上（点E与点B不重合），∠DAE的平分线AF与CD边交于点M，与BC边的延长线交于点F，连接EM. 对于下列四个结论∶①AE=EF；②若CM=CE，则AF=2BC；③若EM⊥AF，则CM=DM；④存在点E，使点 E 与点 D关于直线 AF对称. 其中正确结论的个数为

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（本大题共6小题，每小题3分，共 18分）

13. 若m与-2互为相反数，则m的值为。

查看试题解析
14. 一种细菌半径是1.91×10^-5米，用小数表示为米.

查看试题解析
15. 在一个不透明的盒子里装有5个黑色棋子和若干白色棋子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到白色棋子的概率是 $\frac{2}{3}$ ，则白色棋子的个数为

查看试题解析
16. 如图，已知直线a//b，∠1=50°，∠2=115°，则∠3=

查看试题解析
17. 如图，已知扇形OAB的半径为9，点C在OA上，将△OBC沿BC折叠，点O恰好落在 $\overset{⌢}{A B}$ 上的点D处，且 $l_{\overset{⌢}{A D}} ： l_{\overset{⌢}{B D}}$ =2∶3，若扇形 O4B恰好是一个圆锥的侧面展开图，则该圆锥的底面直径为.

查看试题解析
18. 如图是抛物线y=ax²+bx+c的部分图象，其顶点为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间.下列结论∶①a-b+c>0；②3a+b=0；③b²=4a（c-n）；④关于 x的方程α²+bx+c=n-1有两个不相等的实数根.其中正确结论的序号是

查看试题解析

三、解答题（本大题共8小题，满分66分. 解答应写出文字说明、证明过程或演算步骤

19.

(1)、 $\sqrt{8}$ -（- $\frac{1}{3}$ ）^-2+(2021-π)⁰-4sin45°

(2)、解不等式组 ${\begin{cases} 3 x - 2 < x + 6 \\ \frac{1 - 5 x}{2} \leq 2 - x \end{cases}$ ，并把解集在数轴上表示出来.

查看试题解析
20. 如图，在△ABC中，∠C=90°，AC=4，BC=8.

(1)、用直尺和圆规作AB 边的垂直平分线；（保留痕迹，不写作法）

(2)、若（1）中所作的垂直平分线交 BC 于点D，则 BD的长为

查看试题解析
21. 如图，反比例函数y= $\frac{k}{x}$ （x>0）的图象经过点A（3，4），直线AC与x轴交于点C（6，0），过点C作x轴的垂线 BC交反比例函数图象于点 B.

(1)、求k的值及点 B 的坐标；

(2)、在平面内有点D，使以A，B，C，D 四点为顶点的四边形为平行四边形，请写出所有符合条件的点 D 的坐标.

查看试题解析

22. 某校组织全校学生进行了一次"社会主义核心价值观"知识竞赛，赛后随机抽取了各年级部分学生成绩进行统计，制作如下频数分布表和频数分布直方图。请根据图表中提供的信息，解答下列问题∶

成绩x分	频数	频率
50≤x<60	4	0.1
60≤x< 70	8	b
70≤x<80	a	0.3
80≤x<90	10	0.25
90≤ x<100	6	0.15

(1)、该校随机抽取了名学生的成绩进行统计；

(2)、表中a= ， b= ，并补全频数分布直方图；

(3)、若用扇形统计图描述成绩分布情况，则成绩为60≤x<70所对应扇形的圆心角度数是；

(4)、若该校学生共有 4000人，请估计该校成绩为80≤x<100的学生有多少人?

查看试题解析

23. 突如其来的新冠疫情影响了某商场的经济效益，在复工复产后商场对某种商品价格进行了调整，将该种商品的进价提高了8 元定为销售价格，此时该商品8件的进价恰好相当于6件的售价，且每天可售出200 件，经市场调查发现∶如果该商品每件再涨价 1元，每天就会少售出5件.

(1)、该商品的售价和进价各是多少元?

(2)、若在进价不变的条件下，确保每天所得的销售利润为 2035 元，且销售量尽可能大，则该商品应再涨价多少元?

查看试题解析
24. 如图，点 M在矩形 ABCD的边 AD延长线上，以AM为直径作⊙O 交AC于点F，点E在 CD边上，且 EC=EF.

(1)、求证∶ EF是⊙O的切线；

(2)、若cos∠CAD= $\frac{3}{5}$ ，AF=6，MD=2，求FC的长.

查看试题解析
25. 如图，抛物线 y=-x²+（m-1）x+m（其中m>1）与x轴交于A，B两点，与y轴交于点 C，点 D 在该抛物线的对称轴l上，且 DA=DC.

(1)、点 A 的坐标为，用含m的式子表示点 D的坐标为；

(2)、若△ACD 与△BCO 的面积之比为 5∶ 9，求该抛物线的表达式；

(3)、在（2）的条件下，若动点 P在该抛物线上，且当∠PBC= ∠DAB 时，求点P 的坐标.

查看试题解析
26. 已知∶在△ABC中，AB=AC=4 $\sqrt{2}$ ，∠BAC=90°，AD⊥BC于点D，点E是AC边的中点，动点P在线段 CD上，将线段 PE绕点E逆时针旋转90°得到线段 QE，BQ与AD 交于点p.

(1)、如图 1，当点 P与点C重合时，线段 DF的长为；

(2)、如图 2，当点P与C，D两点均不重合时，
①求证∶PD=2DF；

②问∶是否存在点P，使以P，E，F为顶点的三角形是直角三角形?若存在，请求出 PC 的长；若不存在，请说明理由.

查看试题解析