广东省汕头市2020-2021学年八年级下学期数学月考试卷

试卷更新日期：2021-06-10 类型：月考试卷

进入出卷网下载

一、选择题：（每小题3分，共30分）

1. 下列式子不一定是二次根式的是（）

A、 $\sqrt{a}$ B、 $\sqrt{b^{2} + 1}$ C、 $\sqrt{0}$ D、 $\sqrt{（ a + b ）^{2}}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2}$ + $\sqrt{3}$ ＝ $\sqrt{5}$ B、 $\sqrt{2}$ - $\sqrt{3}$ ＝1 C、 $\sqrt{2}$ ÷ $\sqrt{3}$ ＝ $\frac{\sqrt{6}}{3}$ D、 $\sqrt{2}$ × $\sqrt{3}$ ＝6

查看试题解析
3. 若 $\sqrt{75 n}$ 是整数，则正整数n的最小值是（）

A、2 B、3 C、4 D、5

查看试题解析
4. 若3，m，5为三角形三边，化简： $\sqrt{{(2 - m)}^{2}}$ ﹣ $\sqrt{{(m - 8)}^{2}}$ 得（）

A、﹣10 B、﹣2m+6 C、﹣2m﹣6 D、2m﹣10

查看试题解析
5. 下列四组线段中，能组成直角三角形的是（）

A、a＝2，b＝4，c＝6 B、a＝4，b＝6，c＝8 C、a＝4，b＝8，c＝10 D、a＝6，b＝8，c＝10

查看试题解析
6. 下列命题是假命题的是（）

A、四个角相等的四边形是矩形 B、对角线相等的平行四边形是矩形 C、对角线垂直的四边形是菱形 D、对角线垂直的平行四边形是菱形

查看试题解析
7. 已知三角形的三边长之比为1：1： $\sqrt{2}$ ，则此三角形一定是（）

A、锐角三角形 B、钝角三角形 C、等边三角形 D、等腰直角三角形

查看试题解析
8. 如图所示，在四边形ABCD中，AD∥BC，要使四边形ABCD成为平行四边形还需要条件（）

A、AB＝DC B、∠1＝∠2 C、∠D＝∠B D、AB＝AD

查看试题解析
9. 矩形、菱形、正方形都一定具有的性质是（）

A、邻边相等 B、四个角都是直角 C、对角线相等 D、对角线互相平分

查看试题解析
10. 在下面图形中，每个大正方形网格都是由边长为1的小正方形组成，则图中阴影部分面积最大的是（）

A、 B、 C、 D、

查看试题解析

二、填空题（共7小题，每小题4分，共28分）

11. 计算 $(\sqrt{50} - \sqrt{8}) \div \sqrt{2}$ 的结果是．

查看试题解析
12. 要使式子 $\sqrt{3 - x}$ 有意义，则x的取值范围是．

查看试题解析
13. 直角三角形两直角边长分别为5和12，则它斜边上的高为．

查看试题解析
14. 如图，在平行四边形ABCD中，AD＝3cm，AB＝2cm，则平行四边形ABCD的周长等于．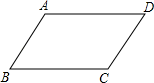

查看试题解析
15. 如图，在平行四边形ABCD中，对角线AC，BD相交于点O，点E是AB的中点，OE＝5，则AD的长为．

查看试题解析
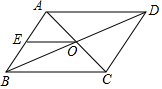16. 已知菱形的两条对角线长为8cm和6cm，那么这个菱形的周长是 cm，面积是 cm² ．

查看试题解析
17. 若 $y = \frac{\sqrt{x - 4} + \sqrt{4 - x}}{2} - 2$ 则 ${(x + y)}^{y}$ .

查看试题解析

三、解答题:(每小题6分，共18分)

18. 计算：

(1)、 $\sqrt{8} + 2 \sqrt{3} - (\sqrt{27} - \sqrt{2})$

(2)、 $\frac{2}{\sqrt{2} - 1} + \sqrt{18} - 4 \sqrt{\frac{1}{2}}$

查看试题解析
19. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

(1)、画线段AD∥BC且使AD=BC，连接CD；

(2)、线段AC的长为， CD的长为， AD的长为.

查看试题解析
20. 先化简，再求值：
$\frac{2 x + 4}{x^{2} - 1} \div \frac{x + 2}{x^{2} - 2 x + 1}$ ，其中 $x = \sqrt{2}$ .

查看试题解析

四、解答题（每小题8分，共24分）

21. 如图，在▱ABCD中，点E、F分别在BC、AD上，且AF=CE．

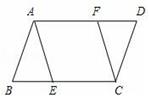
求证：四边形AECF是平行四边形．

查看试题解析
22. 已知：如图，四边形ABCD四条边上的中点分别为E、F、G、H，顺次连接EF、FG、GH、HE，得到四边形EFGH（即四边形ABCD的中点四边形）.

(1)、四边形EFGH的形状是 ▲ ，证明你的结论.

(2)、当四边形ABCD的对角线满足条件时，四边形EFGH是矩形.

查看试题解析
23. 如图，矩形ABCD中，CD=8，AD=4，将矩形沿AC折叠，点D落在点D′处，求重叠部分△AFC 的面积.

查看试题解析

五、解答题（每小题10分，共20分）

24. 已知：如图，在▱ABCD中，O为对角线BD的中点，过点O的直线EF分别交AD，BC于E，F两点，连结BE，DF．

(1)、求证：△DOE≌△BOF；

(2)、当∠DOE等于多少度时，四边形BFDE为菱形？请说明理由．

查看试题解析
25.
已知：如图，在正方形ABCD中，G是CD上一点，延长BC到E，使CE=CG，连接BG并延长交DE于F．

(1)、求证：△BCG≌△DCE；

(2)、将△DCE绕点D顺时针旋转90°得到△DAE′，判断四边形E′BGD是什么特殊四边形，并说明理由。

查看试题解析

广东省汕头市2020-2021学年八年级下学期数学月考试卷

一、 选择题：（每小题3分，共30分）

二、填空题（共7小题，每小题4分，共28分）

三、 解答题:(每小题6分，共18分)

四、解答题（每小题8分，共24分）

五、解答题（每小题10分，共20分）

一、选择题：（每小题3分，共30分）

三、解答题:(每小题6分，共18分)